3.8 Область применения, характеристика и расчет подвижных посадок

Подвижные посадки рассчитываются только для подшипников скольжения. В остальных случаях они выбираются.

Рисунок 3.9 – Расчетная схема подшипника скольжения.

Зазор S,мкм, в состоянии покоя определяют,

S=D-d, (3.39)

где D-номинальный диаметр вкладыша, мм;

d- номинальный диаметр цапфы вала, мм.

При вращении вала зазор S разобьется на две величены: h_{min ,} h_max..Максимальный зазор _, h_max будет равен

_, h_max=S- h_min (3.40)

При вращении вала за счет центробежных сил возникает абсолютный эксэнтрисетет e. Зная абсолютный эксэнтрисетет определяем относительный эксэнтрисетет

Тогда минимальный зазор h_{min ,}мкм, будет равен

. (3.41)

Для обеспечения жидкостного трения необходимо, чтобы минимальный зазор h_min был бы больше или равен толщине масленой пленки h_жт, то есть

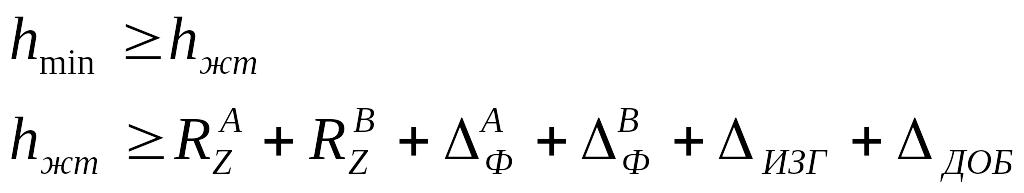, (3.42)

где и - отклонение от геометрической формы, мкм;

– кривизна вала, мкм;

– добавочное отклонение ,мкм.

определить не возможно, тогда толщину масляной пленки h_жт определяют по следующей зависимости

, (3.43)

где k – коэффициент запаса надежности.

Несущая способность подшипника скольжения R, Н, определяется по формуле

, (3.44)

где μ- динамическая вязкость масла, Па*с;

ω – угловая скорость,с^-1;

ψ – относительный зазор,

C_R – безразмерный коэффициент.

Для выбора посадки необходимо знать зависимость толщины масленой пленки h_min от зазора S.

Рисунок 3.10- Зависимость толщины масляной пленки h_жт от величины зазора S.

Удельное давление Р, Па, находят

. (3.45)

С другой стороны C_R зависит от отношения l/d и коэффициента χ. Экспериментальным путем было установлено

Рисунок 3.10

, (3.46)

где k, m – коэффициенты зависящие от l/d.

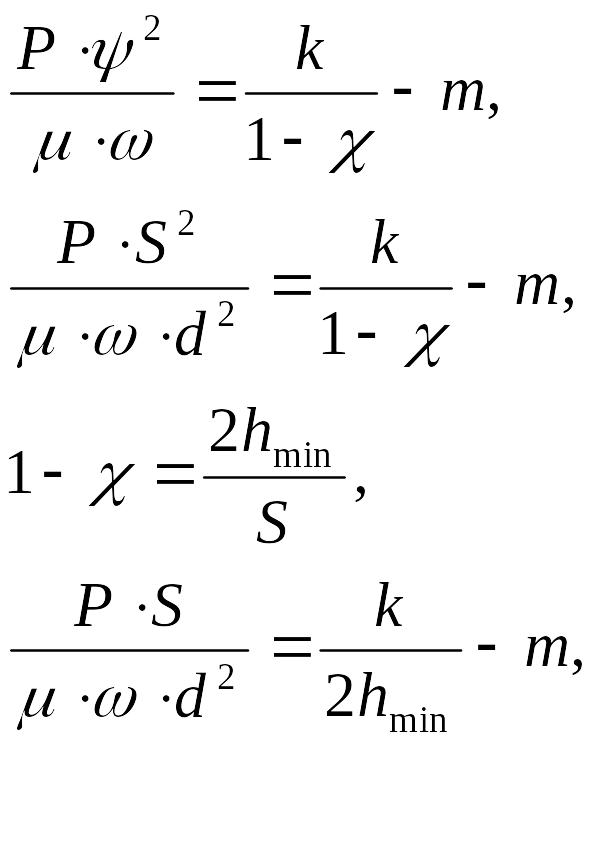(3.47)

Минимальный S^F_min и максимальный S^F_max е зазоры определяют по следующим зависимостям

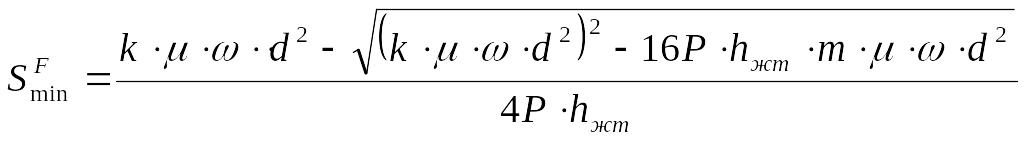, (3.48)

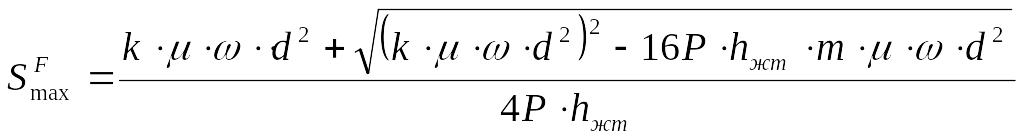, (3.49)

Определив минимальный и максимальный функциональные зазоры выбирают посадку так, что бы

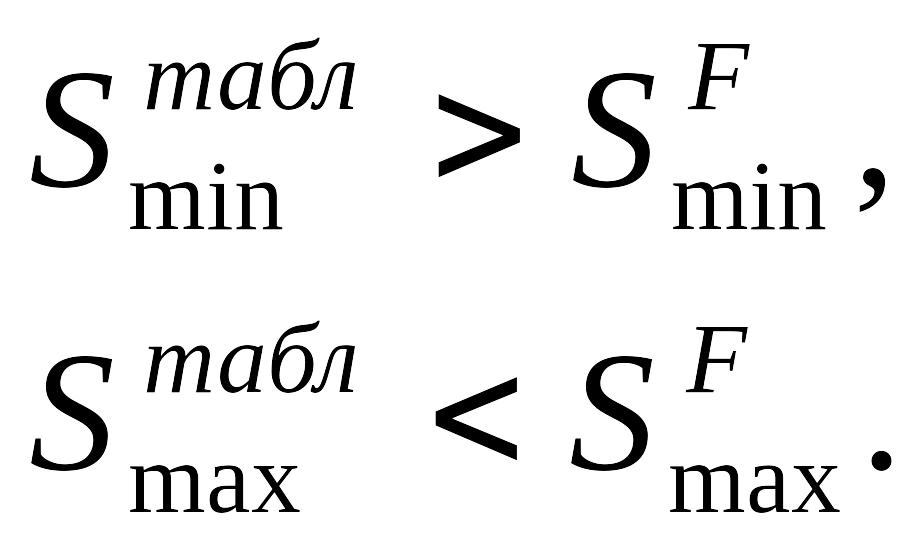(3.50)

После этого проверяют правильность выбранной посадки:

1 .

2 Находим коэффициент С_R.

3 Зная отношение l/d, определяют относительный эксцентриситет χ.

4 Зная χ, определим наименьшую толщину масляной пленки .

5 Зная h_min, из формулы (3.51)определяют коэффициент запаса надежности

(3.51)

(3.52)

Если k₁ ≥2, то посадка выбрана верно.

3.9 Виды измерений, погрешности измерений и средства измерений.

При изготовлении и измерении деталей возникает два вида погрешностей: систематическая и случайная. Систематическими называют погрешности, постоянные по величине знаку или изменяющиеся по определенному закону в зависимости от характера неслучайных факторов. Случайными называются непостоянные по величине и знаку погрешности, которые возникают при измерении и принимают то или иное положение в зависимости от случайно действующих причин. Наличие случайных погрешностей обнаруживается в том, что повторных измерениях получается различный числовой результат. Полностью устранить случайную погрешность невозможно.

Погрешность измерения является суммарной погрешностью, в которую входят погрешности средств измерений, погрешности, связанные с установкой детали, погрешности настройки, влияние температуры и вибрации.

Погрешности измерения могут быть абсолютные _абс,, мм, и относительные _отн, %,

_абс = А-А_ист, (3.53)

где А – результат измерения, мм;

А_ист – истинное значение измеряемой величины,мм.

Отношение _отн= называется относительной погрешностью. Но т. к. истинное значение измеряемой величины не известно, то вместо него принимают результат измерения с полученной погрешностью, которая позволяет приблизиться к истинному значению.

Появление числового значения при измерении рассматривается как случайное событие. Поэтому, чтобы приблизиться к истинному значению, проводят многократные измерения одной и той же величины.

Отношение числа n – случая появления события А к числу N – произведенных измерений называется относительной частотой или частностью события.

При большом числе измерений N частота событий А становится устойчивой. Отношение называется вероятностью.

Зависимость между числовым значением случайной величины и вероятностью их появления установлена законом распределения вероятности случайной величины.

Случайные ошибки всегда соответствуют какому – либо теоретическому закону (их 9).

1Рассеивание значений радиального или торцевого биения подчиняются закону Максвелла.

2Рассеивание отказов работ машин подчиняется закону Вейбеля.

3При равном изменении во времени доминирующего фактора (напряжение, износ инструмента) подчиняется закону равной вероятности.

4

Рисунок 3.11

Рассеивание значений случайной величины, изменение которой зависит от большого числа факторов, но ни один из них не преобладает, то такие ошибки подчиняются закону нормального распределения. Этому закону подчиняется рассеивание погрешностей измерений линейных величин.

Кривая Гаусса

Уравнение кривой Гаусса имеет вид

, (3.54)

где у – частота появления события или плотность распределения вероятностей .

а – координата от начала отсчета до центра группирования размеров, мм;

σ – среднеквадратичное отклонение, мм;

х – случайная величина, мм.

При совпадении центра группирования с началом отсчета величин (а=0)

. (3.55)

В общем случае а=М(х), где М(х) – математическое ожидание случайной величины х.

, (3.56)

где х_i – возможное значение случайной величины.

,

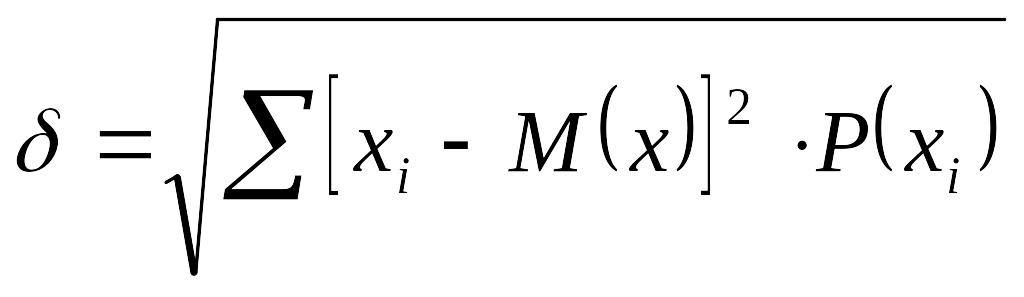где Р(х_i) – частота повторений события.

. (3.57)

Т. К. функция четная, изменим предел интегрирования

. (3.58)

Для удобства при дальнейшем использовании этой формулы в это уравнение вводится новый аргумент z

, (3.59)

тогда

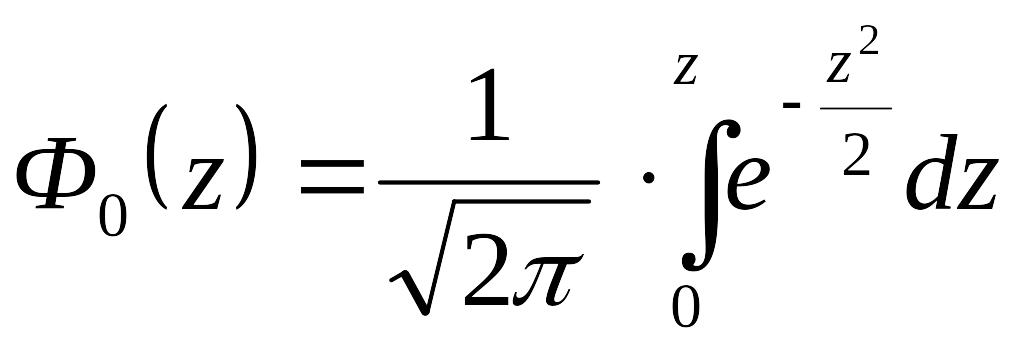. (3.60)

Функция Ф₀(z) называется функцией Лапласа.

При z=0 функция Ф₀=0,при z= Ф₀=0.5, при z=-

Ф₀=-0.5

Анализ формулы показывает, что площадь, ограниченная отрезками z₁ и z₂ и кривой представляет собой вероятность попадания случайной величины в данный интервал.

Если взять х=3σ, тогда z=3. Ф0(3)=0,49865*2=0,99730.

Значение ±3σ служит мерой точности любого станка или прибора.