3.5.2 Обратная задача

В данном случае нам известны номинальные размеры звеньев цепи, а также номинальный размер замыкающего звена, его предельные отклонения и допуск.

Нам необходимо определить допуски составляющих звеньев цепи.

2.1 Определяем среднее число единиц допуска по формуле

, (3.13)

где TA_  допуск замыкающего звена, мм;

A_{i ср.}  средний размер интервала размеров, в который попадает данный действительный размер, мм.

2.2 Зная число единиц допуска, определяют квалитет и назначают допуски размеров согласно этому квалитету для увеличивающих звеньев как отверстие в системе отверстия, а для уменьшающих – как вал в системе вала, затем делают проверку по формуле (3.12), в этом случае возможно два варианта решения

1) TA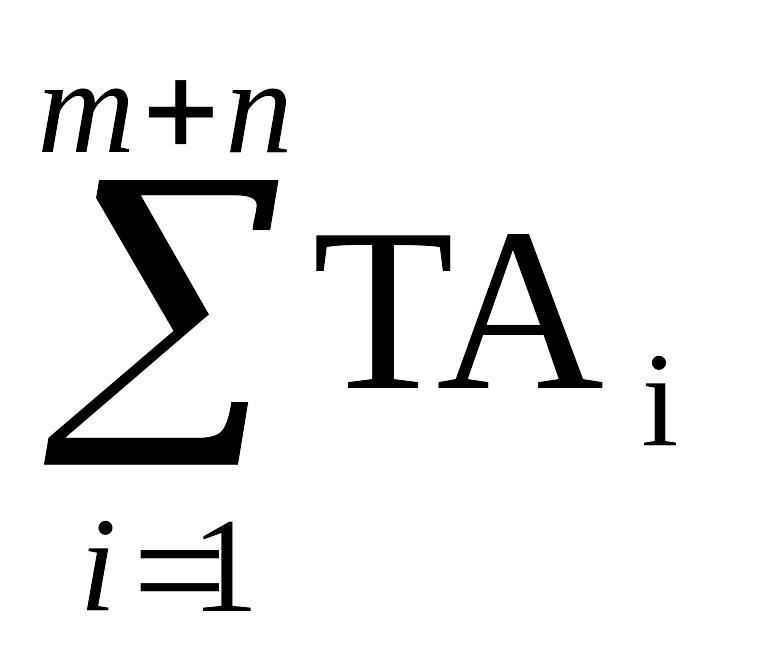_ > (3.14)

2) TA_ < (3.15)

Чтобы равенство (3.12) выполнялось, для первого варианта (3.14), анализируя чертеж и размерную цепь детали (узла) выбирают размер, который наиболее трудно обработать (получить) и назначают на него нестандартный допуск путем прибавления разности TA_ и , к стандартному допуску.

Для второго случая выбирают тот размер, который легко обработать (получить), назначают на него нестандартный допуск, отнимая разность TA_ и от стандартного допуска.

3.6 Решение размерных цепей теоретико-вероятностным методом.

3.6.1 Прямая задача

При выборе предыдущих формул предполагалось, что в процессе обработки или сборки возможно одновременное сочетание наибольшего увеличивающего наименьшего уменьшающего размеров или обратное их сочетание, но такое сочетание маловероятно, т. к. отклонения размеров группируются около середины допуска.

При обработке и сборке деталей возникают случайные и систематические ошибки. Случайные ошибки подчинены закону нормального распределения. Случайные ошибки, как правило, исследуются с доверительной вероятностью 0,9973.

ТА_i= 6A_i , ТА_= 6A_ .

Суммирование случайных погрешностей происходит методом квадратического суммирования

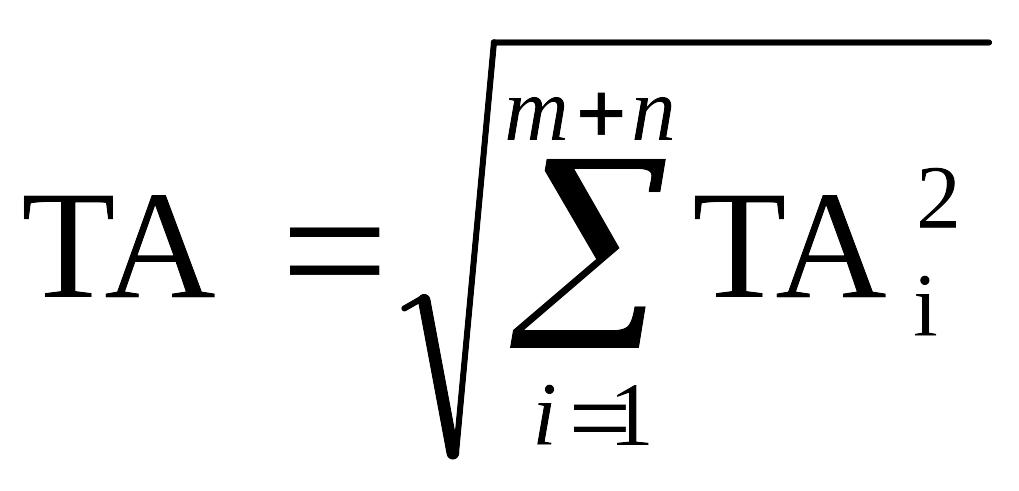, (3.16)

где TA_i − допуск звена, мм.

Формула (3.1) справедлива, если число звеньев в размерной цепи больше шести и если случайные ошибки подчиняются закону нормального распределения. Если число звеньев меньше шести, то допуск замыкающего определяют по формуле

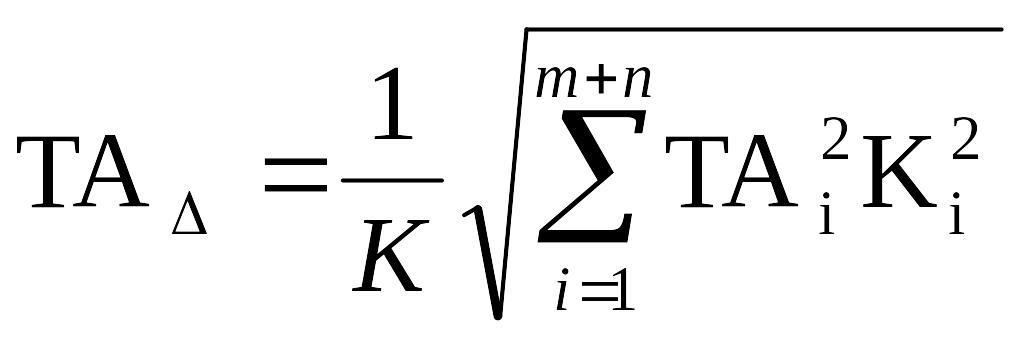, (3.17)

где К − коэффициент, зависящий от числа звеньев в размерной цепи.

К_i − коэффициент, зависящий от закона распределения случайных величин.

К₀=1/3, если (m+n)<6,

К₀=1, если (m+n)<6,

K_i=1 для закона нормального распределения,

K_i=1,72 для закона равной вероятности,

K_i=1,22 для закона треугольника Симпсона.

Верхнее и нижнее отклонения замыкающего звена можно выразить через середину поля допуска

, (3.18)

где Е_с − координата середины поля допуска.

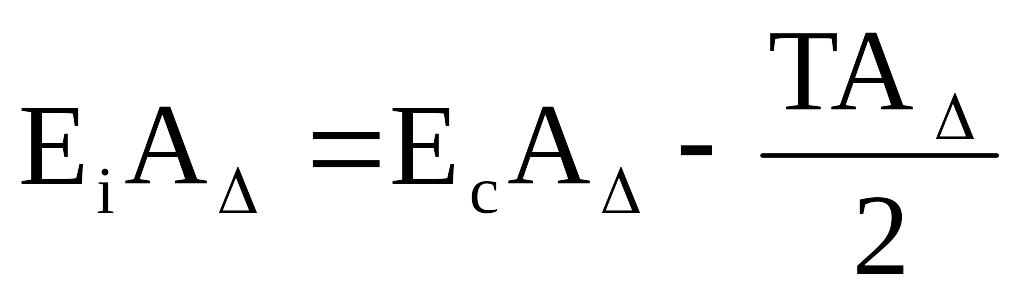, (3.19)

Е_СА_= Е_СА_iув – Е_СА_iум. (3.20)

TAΔ

Рисунок 3.6 − Схема поля допуска замыкающего звена

Проверка выполняется по следующей формуле

.

3.6.2 Обратная задача

В данном случае нам известны номинальные размеры звеньев цепи, а также номинальный размер замыкающего звена, его предельные отклонения и допуск.

2.1 Определяется среднее число единиц допуска по формуле

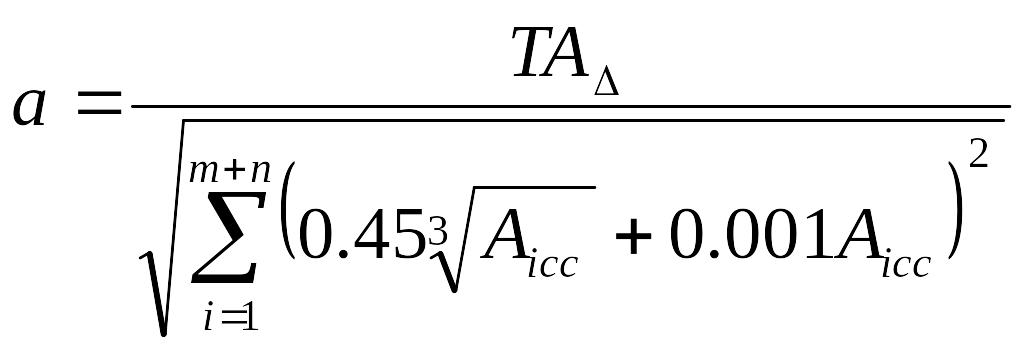, (3.21)

где TA_  допуск замыкающего звена, мм;

A_{i ср.}  средний размер интервала размеров, в который попадает данный действительный размер, мм.

2.3 Зная число единиц допуска, определяют квалитет и назначают допуски размеров согласно этому квалитету для увеличивающих звеньев как отверстие в системе отверстия, а для уменьшающих – как вал в системе вала, затем делают проверку по формуле (3.17), и если равенство не соблюдается, то поступают также как при решении размерных цепей методом максимума − минимума, а именно назначают нестандартный допуск на один из размеров.