3.3 Размерные цепи

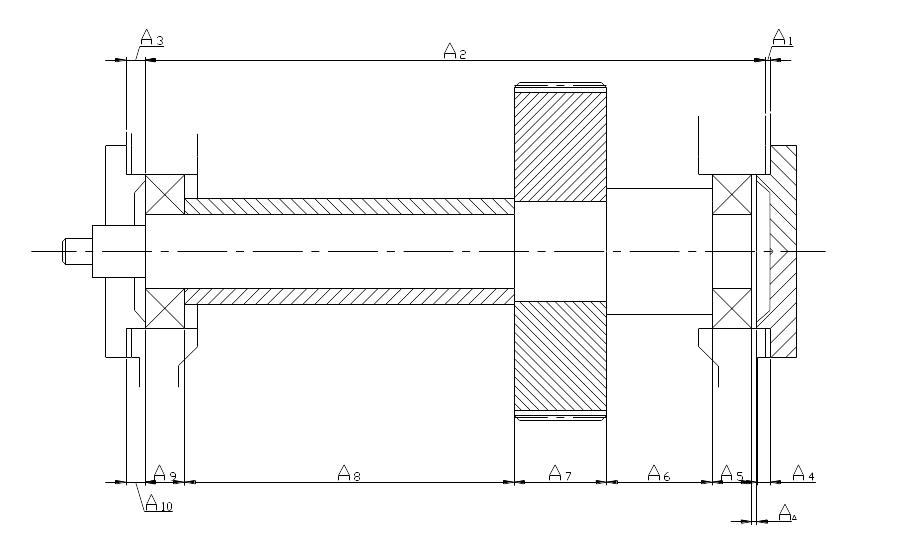
Рисунок 3.4 – Эскиз узла для расчета размерной цепи

Размерной цепью называется совокупность взаимосвязанных размеров (звеньев), расположенных в определенной последовательности по замкнутому контуру определяющих собой взаимное положение осей и поверхностей одной или нескольких деталей в узле или механизме.

По взаимному расположению размеров размерные цепи делятся на:

• линейные,

• плоскостные,

• пространственные.

Размерная цепь называется линейной, если все ее размеры параллельны друг другу и, следовательно, проектируются без изменения величины на две или несколько параллельных линий.

Размерная цепь называется плоскостной, если все или часть размеров, входящих в размерную цепь, не параллельны друг другу, но лежат в одной или параллельных плоскостях.

Размерная цепь называется пространственной, если все или часть размеров, входящих в размерную цепь, не параллельны друг другу и лежат в непараллельных плоскостях.

При решении размерных цепей все размеры обозначаются большими буквами русского алфавита с индексом, который характеризует порядковый номер размеров в цепи.

Размер, получающийся последним в процессе обработки или сборки, величина и точность которого зависит от величины и точности всех остальных размеров цепи, называется замыкающим размером и он имеет индекс . Все остальные размеры называются составляющими.

Размер (звено), с увеличением которого увеличивается и замыкающий размер, называется увеличивающим.

Размер (звено), с увеличением которого уменьшается размер замыкающего звена, называется уменьшающим.

При решении размерных цепей различают две задачи:

1. прямая – когда необходимо определить номинальный размер замыкающего звена, его верхнее и нижнее отклонение и допуск, если известны номинальные размеры всех составляющих звеньев и их допуски;

2. обратная – когда необходимо определить допуски составляющих звеньев, если известны номинальные размеры составляющих звеньев, номинальный размер замыкающего звена, его верхнее и нижнее отклонение и допуск.

Размерные цепи можно решать разными методами.

3.5 Расчет размерных цепей методом максимума- минимума.

3 .5.1 Прямая задача

Рисунок 3.5 – Расчетная схема в графическом изображении

А_ – замыкающее звено, мм;

А₁, А₂, А₃ – увеличивающие звенья, мм;

А₄, А₅, А₆, А₇, А₈, А₉, А₁₀ – уменьшающие звенья, мм.

1. Определяется допуск и отклонение замыкающего звена по допускам составляющих звеньев по справочникам.

1.2 Определяется номинальный размер замыкающего звена А_, мм, по формуле

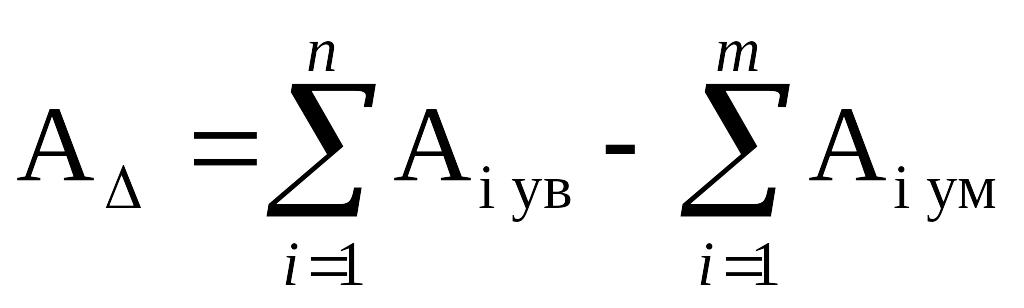, (3.8)

где А_{i ув} – размер увеличивающего звена, мм,

А_{i ум} – размер уменьшающего звена, мм,

n  количество увеличивающих звеньев,

m – количество уменьшающих звеньев.

1.3 Определяется наибольший предельный размер замыкающего звена А^нб_, мм, по формуле

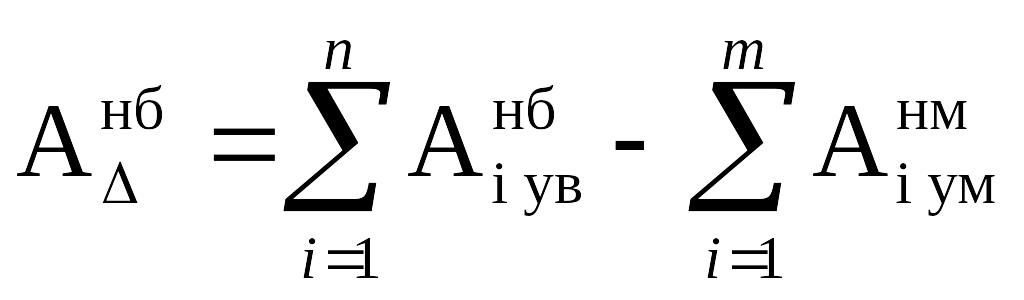, (3.9)

где  наибольший предельный размер увеличивающего звена, мм;

 наименьший предельный размер уменьшающего звена, мм.

1.4 Определяется наименьший предельный размер замыкающего звена А^нм_, мм, по формуле

,

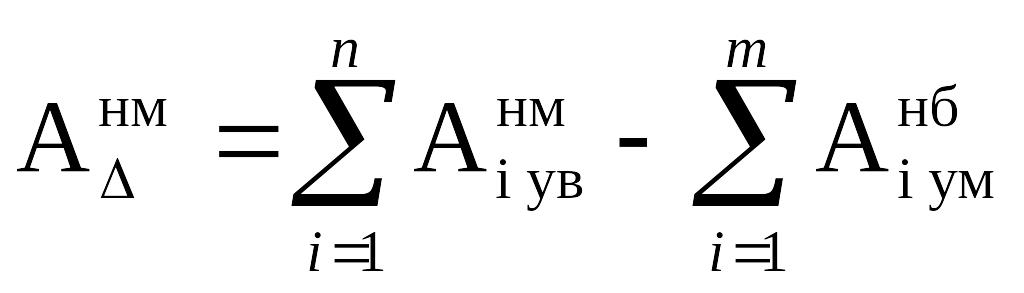где  наименьший предельный размер увеличивающего звена, мм;

 наибольший предельный размер уменьшающего звена, мм.

1.5 Определяется верхнее отклонение предельного размера E_sA_, мм, нижнее отклонение предельного размера E_iA_, мм, замыкающего звена по следующим формулам

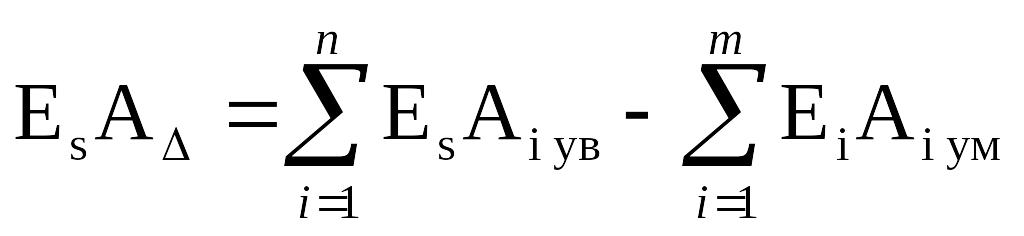, (3.10)

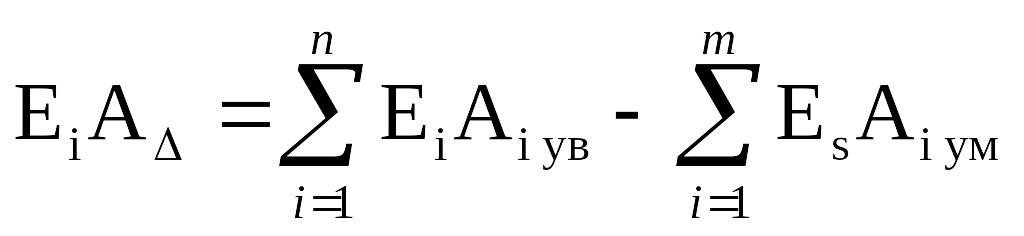, (3.11)

где E_s  верхнее отклонение, мм;

E_i  нижнее отклонение, мм.

1.6 Допуск замыкающего звена ТА_, мм, определяется по следующей зависимости

ТА_= E_sA_ E_iA_,

1.7 Проверка производится по следующей формуле

, (3.12)