Глава 3. Имитационное моделирование деятельности предприятия

в детерминированном и недетерминированном случае

3.1. Построение базовой модели деятельности предприятия в среде EXCEL

Реализуем на основе программного комплекса MS Excel базовую модель хозяйственной деятельности предприятия.

Настоящая модель основывается на следующих основных предположениях:

1. Финансовые ресурсы предприятия зависят от объема произведенной продукции в текущий момент времени t и предыдущие периодов: t-1, t-2, …, t-m.

2. Товар продается в течение определенного времени (в рамках данного практикума в течение 3 шагов), скорость продажи товара задается вектором a/

3. Доход вычисляется, как произведение количества проданной продукции Q на цену P единицы продукции - Q*P.

4. На оборот (объем продаж) начисляется налог с коэффициентом налогообложения q

Для расчета объема производства с использованием базовой модели (2.5) зададим следующие значения:

1. Переменные затраты (EV=2$, в любой момент времени t).

2. Постоянные затраты (EC=1000$ в любой момент времени t).

3. Срок жизни товара (m=3).

4. Уровень цен (P=5$).

5. Инвестиции (F_t=500 000$ в времени t=1, далее F_t=0)

6. Вектор скорости продаж (a=0,55; 0,2;0,1)

7. Размер оборотных налогов (q=0.1).

8. Размер подоходных налогов (r=0.2)

Рассчитываются с использованием динамической модели:

1. Оборотный налог в период времени t: .

2. Подоходный налог в период времени t: .

3. Продажи: .

4. Оборотные средства предприятия: .

5. .Объем производства Q_t:

Q_t = VR_t/ EV_t.

Создадим шаблон решения задачи (рис. 3.1.1) и запишем формулы в соответствии с таблицей 3.1.1:

Рис. 3.1.1. Шаблон решения задачи

Таблица 3.1.1

Необходимые формулы

Ячейка	Формула	Примечание
D10	=$B$10*D18	Далее копируем формулу в диапазон E10: O10
D11	=ЕСЛИ(D18>(C20*D6+D5);$B$11*(-(C20*D6+D5)+D18);0)	Далее копируем формулу в диапазон E11: O11
D18	=C20*E9*D15
E18	=(D20*E9+C20*D9)*D15
F18	=(E20*$E9+D20*$D9+C20*$C9)*$D$15	Далее копируем формулу в диапазон G18:O18
	При заполнении первых трех столбцов нужно помнить что первый столбец зависит только от нулевого столбца, второй только от нулевого и первого, третий только от первого второго и третьего, начиная с четвертого каждый столбец зависит от четырех предыдущих.
D19	=D18+D14-$D$5-D10-D11	Далее копируем формулу в диапазон E19: O19
D20	=D19/D6	Далее копируем формулу в диапазон E20: O20
E21	=(E20-D20)/D20	Далее копируем формулу в диапазон F21: O21

Построим модель с комбинированным вектором реинвестирования (2.9):

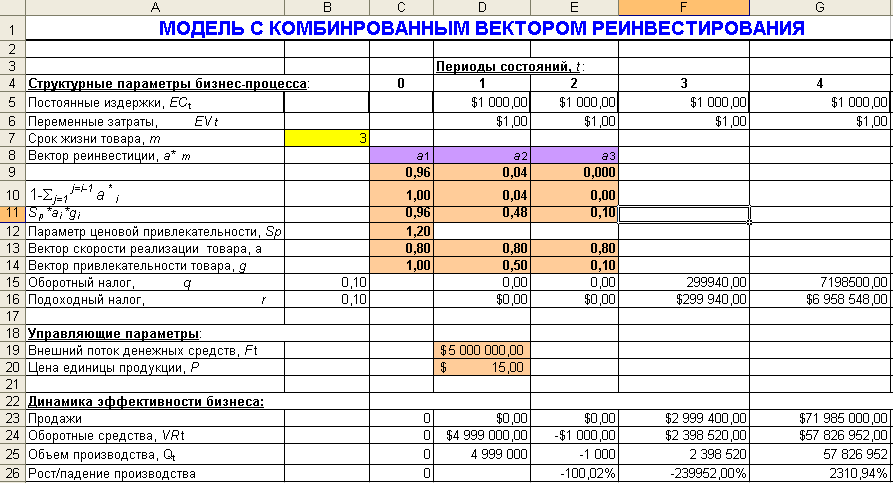
Рис. 3.1.2. Шаблон решения задачи с комбинированным вектором реинвестирования

Для расчета объема производства с использованием модели (2.9) зададим следующие значения:

1. Переменные затраты (EV=1$, в любой момент времени t).

2. Постоянные затраты (EC=1000$ в любой момент времени t).

3. Срок жизни товара (m=3).

4. Уровень цен (P=15$).

5. Инвестиции (F_t=5 000 000 $ в времени t=1, далее F_t=0, т.е. весь объем денежных средств инвестируется на первом шаге).

6. Вектор скорости продаж (a=0,8; 0,8;0,8).

7. Вектор привлекательности товара (g=1;0,5;0,1).

8. Параметр ценовой привлекательности (S_p=1,2).

9. Размер оборотных налогов (q=0,1).

10. Размер подоходных налогов (r=0,2)

Для расчета вектора реинвестиции зададим следующие формулы (таблица 3.1.2).

Таблица 3.1.2

Ячейка	Формула	Примечание
C11	=$C$12*C13*C14	Далее копируем формулу в диапазон D11: E11. В диапазоне C11: E11 вычислено
C10	=1-B9	Далее копируем формулу в диапазон D10: E10. В диапазоне C10: E10 вычислено
C9	=МИН(C10:C11)	Далее копируем формулу в диапазон D9: E9. В диапазоне C9: E9 вычислено значение вектора реинвестирования

Управление предприятием на базе модели (2.9) осуществляется варьированием следующих параметров: внешний поток денежных средств на шаге t – F_t и цена единицы продукции P.

Используем построенную модель для решения следующих задач:

1. При каком значении цены и фиксированном объеме инвестиций (5 000 000$) объем производства через год достигнет 1 000 000 (ед)? (р=1,36)

2. При каком объеме инвестиций в оборотные средства и фиксированной цене =1.36 $ объем производства через год достигнет 1 000 000 (ед)? (F= 5 000 000$)

Рассмотрим технологию решения задачи 1. Используем функцию Подбор параметра, меню Сервис. Диалоговое окно Подбор параметра выглядит следующим образом (рис. 3.1.3), величины, находящиеся в ячейках описаны в таблице 3.1.3.

Рис. 3.1.3. Диалоговое окно Подбор параметра

Таблица 3.1.3

Ячейка	Величина
O25	Объем производства в конце года
$D$20	Цена ед продукции

3.2. Построение модели деятельности предприятия, учитывающей закон убывающей производительности капитала в среде EXCEL

Построим модель с учетом закон убывающей производительности капитала, используя со следующие данные

1. Переменные затраты (EV=1$, в любой момент времени t).

2. Постоянные затраты (EC=1000$ в любой момент времени t).

3.Срок жизни товара (m=4).

4. Уровень цен (P=5 $).

5. Инвестиции (F_t=1 000 000 $ в времени t=1, далее F_t=0, т.е. весь объем денежных средств инвестируется на первом шаге).

6. Вектор скорости продаж (a=0,6; 0,6;0,6;0,6).

7. Вектор привлекательности товара (g=1;0,5;0,1).

8.Параметр ценовой привлекательности (S_p=1).

9. Размер оборотных налогов (q=0,1).

10. Размер подоходных налогов (r=0,2)

11. EVinc = 0,91.

Исследуем модель при F= 10 000; 20 000; 30 000; 40000; 50000;60 000; 70 000 (рис. 3.3.1).

Очевидны следующие факты: скорость роста новой модели имеет более медленный характер по сравнению со старой; в новой модели, даже значительное увеличение финансовых вложений на первом шаге не приводит к значительному увеличению объема производства в перспективе. Так, объем производства при F= 50000 уже значительно ниже, чем при F= 40000.

Рис. 3.3.1 Исследование зависимости объема производства от увеличения финансовых вложений

Таким образом, полученная модель имеет потенциально более широкую область применения, поскольку может использоваться для моделирования поведения предприятия не только на первом этапе взрывного роста, но и для построения оценок эффективности предприятия в средне- и долгосрочной перспективе. Кроме того, тот факт, что финансовые вложения сверх определенного предела приносят предприятию все меньше и меньше пользы, позволяет более адекватно оценивать эффективность привлечения заемных финансовых ресурсов.

Еще одним значительным достоинством новой модели является то, что с ее помощью можно попытаться ответь на вопрос, «Когда наступает время выводить денежные средства из предприятия»? Поскольку эффективная доходность вложений в деятельность предприятия падает, то по достижении некоторой критической отметки (например, доходности по банковским депозитам) владельцы предприятия могут принять решение либо о модернизации/расширении производства, что изменит структурные параметры предприятия и уменьшит эффективные издержки, либо об изъятии прибыли путем, например, выплаты дивидендов.

3.3. Изучение влияния помехи на результаты моделирования

При моделировании реального предприятия, кроме проблемы идентификации параметров, остро встает и другая проблема – моделирования в условиях неопределенности. Для большинства предприятий невозможно гарантировать, что ситуация на рынке останется неизменной в течение всего периода моделирования. Особенно резко эта проблема стоит для моделирования в течение длительного времени. В том случае, если нам известны некие прогнозы изменения тех или иных параметров конкурентной среды, мы можем учесть это в модели, используя вместо фиксированных переменных векторы, размерностью совпадающие с длительностью моделирования. То есть, записать модель 2.11 в виде

и задать в качестве условий вектора

Такой способ позволяет моделировать деятельность предприятия в условиях изменяющейся внешней среды, но лишь в том случае, когда нам известны априори эти изменения. К сожалению, такое случается достаточно редко. В этой связи, как правило, делается предположение о том, что изменение некоторого параметра является случайным.

Как правило, предполагается, что значение параметра на шаге t представляет собой случайную величину, распределенную либо равномерно, либо согласно нормальному закону распределения и имеющую математическое ожидание, равное либо базовому значению, либо значению на предыдущее шаге. Этот способ можно комбинировать с имеющимися прогнозами изменения параметров, предполагая математическое ожидание, равное прогнозному значению. Воздействие случайности на результаты моделирования принято называть помехой, а использование случайных значений какой-либо величины – применением помех к этой величине. Как правило, помеха применяется к цене и переменным издержкам, реже - к постоянным издержкам и крайне редко - к значениям налоговых ставок.

Влияние помехи на результаты моделирования

Использование стохастического подхода к моделированию не только позволяет осуществлять моделирование в условиях неопределенных параметров, но и позволяет использовать модель для исследования устойчивости предприятия к воздействиям рыночной среды. В отличие от детерминированного подхода, когда для получения результатов моделирования требовался один цикл вычислений, в недетерминированном случае количество вычислений резко возрастает, так как для относительно точной оценки результатов требуется моделирования ста и более циклов вычисления. Полученные результаты усредняются для получения итоговой оценки. Для оценки достаточности количества циклов моделирования необходимо сравнивать результаты нескольких экспериментальных серий, различия между полученными результатами стремятся к нулю при увеличении количества испытаний в каждой серии. В том случае, если различия между сериями с точки зрения организатора являются достаточно малыми, наращивание количества испытаний в каждой серии можно прекратить.

Степень разброса результатов моделирования существенно зависят от дисперсии случайных величин, задающих параметры модели. Чем больше дисперсия, тем большее количество циклов моделирования потребуется для получения приемлемых результатов.

Стохастический подход позволяет оценить вероятность наступления того или иного события (например, разорения или выхода на заданный уровень производства). Для этого необходимо произвести серию экспериментов и усреднить значение функции критерия (функция, принимающая значение 1 в случае наступления исследуемого события и 0 - иначе) по количеству испытаний в серии. Полученная величина будет являться вероятностью наступления события. Принцип определения необходимого количества испытаний в каждой серии моделирования аналогичен случаю определения количества испытания для получения средних значений.

Рассмотрим результаты предприятия, определяемого следующим параметрами

в условиях помехи различной силы, примененной к переменным издержкам, мы будем рассматривать нормально распределенную помеху с математическим ожиданием . При этом, во избежание возникновения неопределенности, дополнительно потребуем, чтобы значение переменных издержек было больше некоторой положительной величины, например .

При этом рассмотрим поведение предприятия в условиях помехи различной силы (рис. 3.3.1):

• слабая помеха

• средняя помеха

• сильная помеха

При моделировании предполагалось, что все финансовые средства поступают предприятию единовременно на первом шаге.

Рис. 3.3.1 Помехи, применяемые при моделировании

Объем производства на 12 шаге, в зависимости от величины помехи представлен в таблице 3.3.1

Таблица 3.3.1

ПОМЕХА	Объем производства, Qt, на 12 шаге
Сильная	368 928
Средняя	357 452
Слабая	360 835

Исходя из данных моделирования, предприниматели, имеющие достаточный объем денежных средств, должны искать максимально рисковые рынки и получать на них значительную прибыль практически без риска для своих вложений. Такие выводы, безусловно, лишены экономического смысла и требуют модификации недетерминированного подхода к построению модели.

49