Решение задачи с помощью графического способа

Решение этой задачи может быть получено графически. Используем программу для построения графиков Advanced Grapher. Для этого вбиваем формулы ограничений (16) и уравнение ЦФ (18).

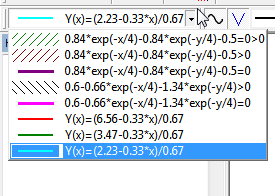
Рис. 1. Работа с Advanced Grapher. Перечень графиков.

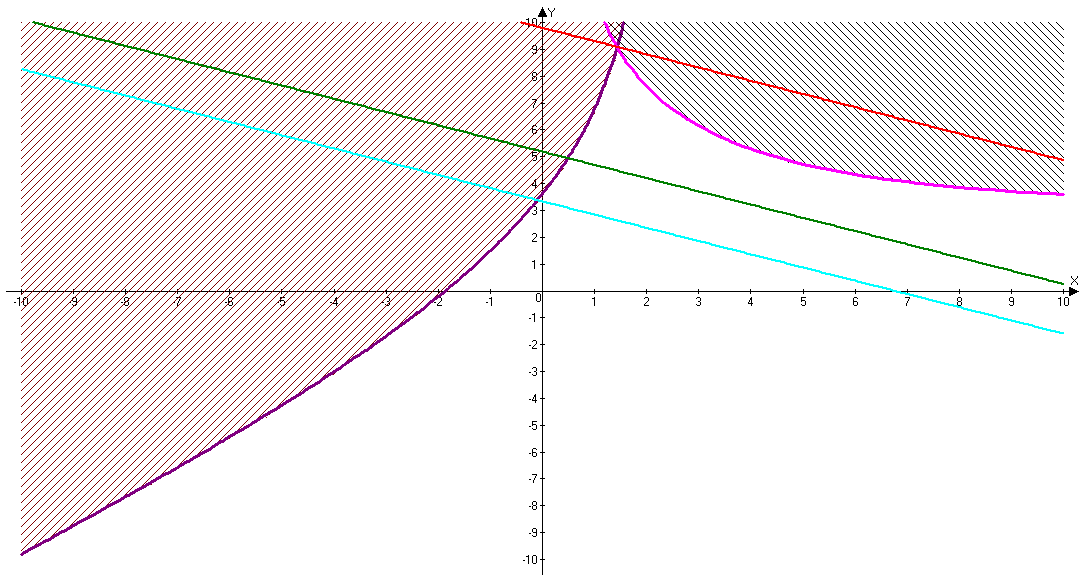
Рис.2. График построения линий уровня

Целевая функция имеет вид: ₍₁₉₎

Для того чтобы максимизировать ее значение, необходимо, что бы значения x и y стремились к нулю. Так, выбираю оптимальную линию уровня, уравнение которой выглядит следующим образом:

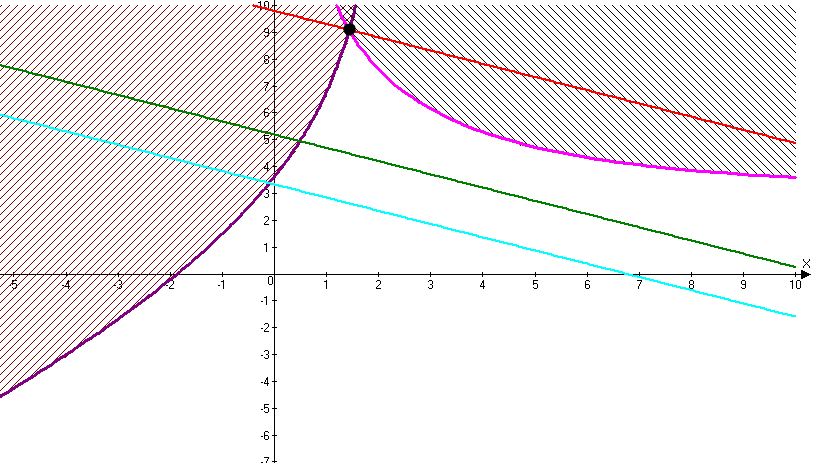
Рис. 3. Искомая точка и её координаты.

Соблюдая все ограничения, находим точку пересечения двух областей и ЦФ, координаты которой: (1,44; 9,1).

Для того, чтобы убедиться в достоверности полученных координат, составим и решим систему:

	0,84*e-x/4-0,84*e-y/4-0,5=0
	0,6-0,66*e-x/4-1,34*e-y/4=0

Сделаем замену: e^-x/4=x1; e^-y/4=x2

Перепишем систему уравнений в матричном виде и решим его методом Гаусса:

	0.84	-0.84	0.5
	-0.66	-1.34	-0.6

1-ую строку делим на 0.84

	1	-1	25/42
	-0.66	-1.34	-0.6

от 2 строк отнимаем 1 строку, умноженную соответственно на -0.66

	1	-1	25/42
	0	-2	-29/140

2-ую строку делим на -2

	1	-1	25/42
	0	1	29/280

от 1 строк отнимаем 2 строку, умноженную соответственно на -1

	1	0	587/840
	0	1	29/280

Ответ:

	x1 = 587/840
	x2 = 29/280

Возвращаемся к исходным переменным:

e^-x/4=0,7 и e^-y/4=0,1

x=1,44 y=9,1

Результаты решения системы совпадают с результатами, полученными в результате построения графиков в программе Advanced Grapher, следовательно, координаты искомой точки найдены верно.

Решение задачи с помощью надстройки «Поиск решения»

Решим задачу нелинейного программирования с помощью надстройки «Поиск решения». В ячейках G5: H5 будут находиться значения искомых величин x и y. В ячейке I11 и I17 содержится значение целевой функции, которое равно значению функции полезности для принципала при высоком и низком уровне усилий агента, т.е. ожидаемая прибыль фирмы. В ячейке F3 содержится альтернативное значение полезности для агента.

В ячейках I10 и I16 вычислим ожидаемую полезность для агента при высоком и низком уровнях усилий соответственно.

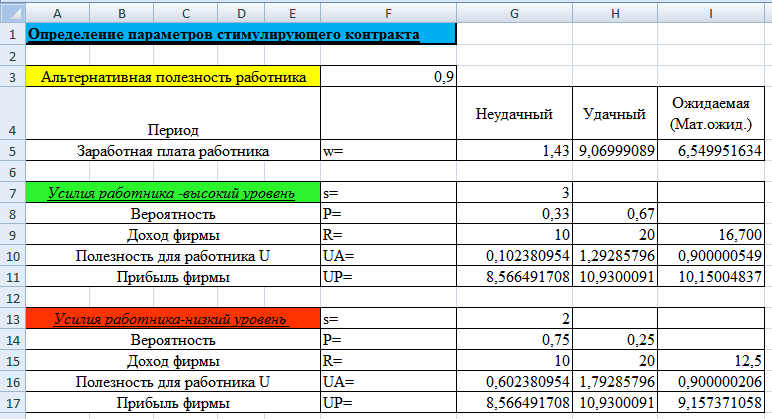Рис. 4. Фрагмент электронных таблиц MS Excel в режиме отображения данных

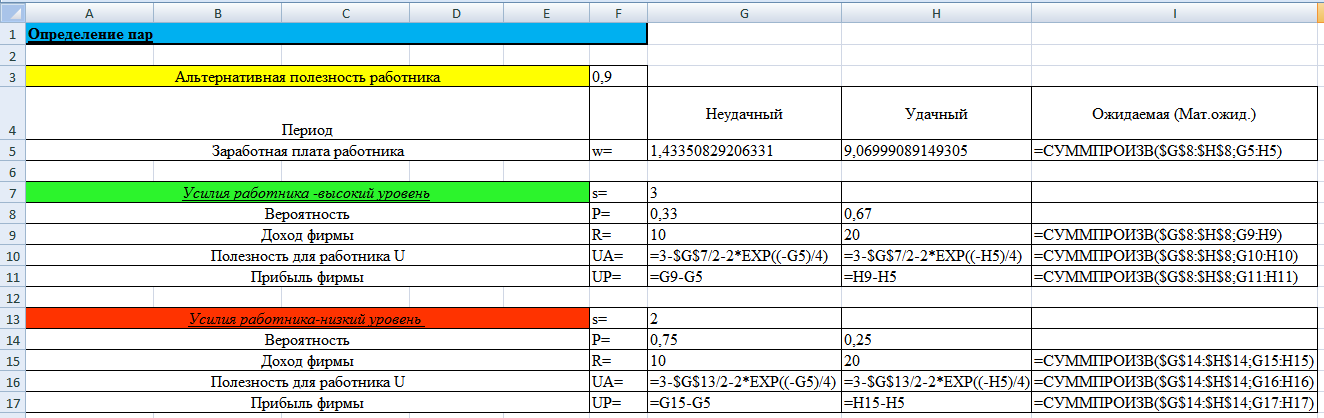Рис. 5. Фрагмент электронных таблиц MS Excel в режиме отображения формул

Для проведения оптимизации используем надстройку «Сервис» - «Поиск решений». В ячейке I11 содержится ожидаемая прибыль фирмы, которая равна значению функции полезности для принципала при высоком уровне усилий агента и оптимальных значениях стимулирующего контракта, она равна 10,15. Найденные значения величин x и y, а также ожидаемой прибыли совпадает с решением найденным графически.