2.5.3 Определение геометрических характеристик сечения продольных рёбер

Сечение ребристой панели приводим к эквивалентному (по площади и моменту инерции) тавровому сечению.

Рисунок 2.6 - Поперечное сечение продольного ребра плиты

Площадь бетонного сечения плиты:

А_с= , (26)

где А_сi - площадь сечения i-го элемента,

А_с= 2·(147,5·4+41·8,5+24·1,5+5,5·41/2)=2175 см².

Статический момент бетонного сечения (относительно оси, проходящей по нижней грани сечения):

S_с= , (27)

где y_сi – расстояние от оси, проходящей по нижней грани сечения до центра тяжести сечения i-го элемента.

S_с=2·(147,5·4·43+41·8,5·41/2+24·1,5·12+5,5·41/2·2/3·41)=72056 см³.

Расстояние от нижней грани до центра тяжести бетонного сечения:

z_с= S_с/А_с=72056/2175=33,1 см

Расстояние от верхней грани до центра тяжести бетонного сечения:

h-z_с=45-33,1=11,9 см.

Момент инерции бетонного сечения (относительно горизонтальной оси, проходящей через центр тяжести бетонного сечения):

I_с= , (28)

где I_xi – момент инерции сечения i-го элемента относительно горизонтальной оси, проходящей через центр тяжести всего бетонного сечения,

a_i – расстояние от горизонтальной оси, проходящей через центр тяжести всего бетонного сечения, до горизонтальной оси, проходящей через центр тяжести сечения i-го элемента.

I_с=2·(147,5·4³/12+147,5·4·(11,9-4/2)²+8,5·41³/12+8,5·41·(33,1-

-41/2) ² + 1,5·24³/12+1,5·24·(33,1-24/2) ²+5,5·41³/36+5,5·41/2·(33,1-41·2/3) ²)=

=389588 см⁴

Отношение модулей упругости (см. п.2.1):

α_с=Е_s/Е_с=200000/36900=5,42.

Приведенная площадь сечения:

А_с'=А_с+α_с·А_st=2175+5,42·5,09=2203 см²

Статический момент инерции приведенного сечения относительно нижней грани ребра:

S_с' = S_с+α_с·S_st = 2·(147,5·4·43+41·8,5·41/2+24·1,5·12+5,5·41/2·2/3·41+ 5,42·2,545·5)=72194 см³.

Расстояние от нижней грани до центра тяжести приведенного сечения:

z_с= S_с'/А_с'=72194/2203=32,8 см.

Расстояние от верхней грани до центра тяжести приведенного сечения:

h-z_с=45-32,8=12,2 см.

Расстояние от точки приложения силы обжатия до центра тяжести приведенного сечения:

z_ср=z_с-с=32,8-5=27,8 см.

Момент инерции приведенного сечения:

I_с'= =2·(147,5·4³/12+147,5·4·(12,2-4/2)²+8,5·41³/12+8,5·41·(32,8-

-41/2) ² + 1,5·24³/12+1,5·24·(32,8-24/2) ²+5,5·41³/36+5,5·41/2·(32,8-41∙2/3) ²+

+5,42·2,545·(32,8-5) ²)=405647 см⁴

Момент сопротивления:

-относительно нижней грани

W_с=I_с'/z_с=405647/32,8=12367 см³.

-относительно верхней грани

W_с=I_с'/(h-z_с)=405647/12,2=33249 см³.

Внешний периметр поперечного сечения плиты:

U=2·( b_f′+2·h- h_f′)=2·( 295+2·45-4)=762 см.

2.5.4 Определение потерь предварительного напряжения в арматуре

Нормы по проектированию железобетонных конструкций устанавливают следующие условия назначения величины предварительного напряжения для стержневой арматуры:

_0,max+p≤ 0,9·f_pk,

_0,max-p≥ 0,3·f_pk. (29)

где _0,max-начальное контролируемое предварительное напряжение арматуры;

р - максимально допустимое отклонение значения предварительного напряжения, вызванное технологическими причинами (р=0,05∙_0,max при механическом способе натяжения арматуры);

f_pk – нормативное сопротивление напрягаемой арматуры ( для стали S1200 f_pk=1200 МПа).

_0,max=(0,5…0,9)·f_pk=(0,5…0,9)·1200=600…1080 МПа

Принимаем _0,max=8400 МПа, тогда р=0,05·840=42 МПа.

Условия

_0,max+p=8400+42=882 МПа≤ 0,9·1200=1080 МПа,

_0,max-p=840-42=798 МПа≥ 0,3·1200=360 МПа.

выполняются.

Определяем потери предварительного напряжения в напрягаемой арматуре.

Технологические потери (первые потери в момент времени t=t₀).

1. 1.Потери от релаксации напряжений арматуры при механическом способе натяжения, для стержневой арматуры:

ΔP_ir=(0,1·_i,max-20)· А_p , (30)

ΔP_ir=(0,1·840-20)· 509= 32,576 кН

2. 2.Потери от температурного перепада, определяемого как разность температур натянутой арматуры в зоне нагрева и устройства , воспринимающего усилие натяжения при прогреве бетона, для бетона класса С30/37 следует рассчитывать по эмпирической формуле:

ΔP_ΔТ=1,25·ΔТ·А_sp , (31)

где - разность между температурой нагреваемой арматуры и неподвижных упоров (вне зоны прогрева), воспринимающих усилие натяжения, °С , при отсутствии точных данных допускается принимать =65°С.

ΔP_ΔТ=1,25·65·509=41356 Н=41,36 кН.

3. Потери, вызванные деформациями стальной формы. Поскольку данные о технологии изготовления изделий и конструкции формы отсутствуют, потери усилия предварительного напряжения от ее деформаций принимаем равными ΔP_f=30·A_p=30·509=15270 Н=15,27 кН

4. Потери, вызванные трением напрягаемой арматуры об огибающие приспособления, принимаем равными нулю, т.к. напрягаемая арматура прямолинейна

ΔP_µ(x)=0.

5. Потери от деформации анкеров

ΔP_А=(Δl/l)·E_s·А_sp, (32)

где l=8,5 м – длина натягиваемого стержня (расстояние между наружными гранями стенда)

Δl – обжатие опрессованных шайб, смятие высаженных головок и т.п., принимаемое равным 2 мм.

ΔP_А=(2/8500)·200000·509=23953 Н=23,95 кН.

6. Потери, вызванные упругой деформацией бетона, при натяжении на упоры определяем по формуле:

ΔP_с= α·ρ_р·(1+ z_ср²·А_с/I_с)· P_0с, (33)

где ρ_р – коэффициент армирования сечения:

ρ_р=А_р/А_с, (34)

ρ_р=5,09/2175=0,0023.

α=Е_s/Е_с=200000/35100=5,7 – отношение модулей упругости стали и бетона.

z_ср=32,8-5=27,8 см - расстояние между центрами тяжести бетонного сечения и напрягаемой арматуры,

Р_0с - усилие предварительного напряжения с учетом потерь, реализованных к моменту обжатия бетона.

Р_0с=_0,max·А_sp- ΔP_ir - ΔP_ΔТ - ΔP_f - ΔP_А=840·509/1000 – 34,576 – 41,36 – 15,27 - 23,95=382,44 кН.

ΔP_с= 5,7·0,0023·(1+ 27,8²·2175/389588)· 382,44=24,91 кН.

Согласно [1, п.9.1.6], должно выполняться условие:

_pm,0 ≤0,75·f_pk,

где _pm,0 - начальные напряжения в напрягаемой арматуре непосредственно после передачи натяжения на бетон.

Т.к. Р_m,о=_pm,0·А_p,то усилие предварительного обжатия Р_m,о, действующее непосредственно после передачи усилия предварительного обжатия на конструкцию должно быть не более:

Р_m,о ≤0,75·f_pk·А_p, (35)

Р_m,о= Р_0с-ΔP_с=382,44-24,91=357,53 кН.

357,53 кН<0,75·1200·509=458,1 кН – условие выполняется.

Максимальные напряжения в бетоне в момент обжатия

σ_с=Р_m,о/А_с+ Р_m,о·z_ср·z_с/I_с, (36)

σ_с=357,03/2203+357,03·27,8·32,8/405647=0,903 кН/см²=9,03 МПа,

Условие

σ_с=9,03 МПа<0,75∙f_cm=0,75∙28=21 МПа выполняется.

Здесь f_cm- средняя прочность бетона в момент обжатия (см. п.2.1)

Эксплуатационные потери (вторые потери в момент времени t>t₀₎:

Реологические, вызванные ползучестью и усадкой бетона, а также длительной релаксацией напряжений в арматуре:

(37)

где - потери предварительного напряжения, вызванные ползучестью, усадкой и релаксацией;

(38)

где

- ожидаемые относительные деформации усадки бетона к моменту времени t;

(39)

здесь:

- физическая часть усадки при испарении из бетона влаги, определяемая по табл. 6.3[1] методом линейной интерполяции при и , .

- химическая часть усадки, обусловленная процессами твердения вяжущего;

(40)

здесь:

=0,865;

,

;

- коэффициент ползучести бетона за период времени, от t₀ до t=100 суток . При см<10см (где U- периметр сечения, см. п.2.5.2) ; принимаем см, по графику =1,9;

- напряжения в бетоне на уровне центра тяжести напрягаемой арматуры от практически постоянной комбинации нагрузок, включая собственный вес;в формуле (49) учитываются со знаком «-», т.к. являются растягивающими;

, (41)

МПа

- начальное напряжение в бетоне на уровне центра тяжести напрягаемой арматуры от действия усилия предварительного обжатия;

, (42)

МПа.

- изменение напряжений в напрягаемой арматуре в расчетном сечении, вызванные релаксацией арматурной стали, для вычисления которых сначала определяем - напряжения в арматуре, вызванные натяжением (с учетом первых потерь в t=t₀) и от действия практически постоянной комбинации нагрузок.

(43)

МПа.

Принимая при и для третьего релаксационного класса арматуры потери начального предварительного напряжения от релаксации арматуры составляют 1,5%, тогда

МПа;

Т.к. 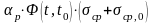=5,7·1,9·(-5,6+1,72)<0, то данную величину принимаем равной нулю.

МПа;

Н=34,66 кН

Среднее значение усилия предварительного обжатия Р_m.t в момент времени t>t₀ ( с учетом всех потерь) при натяжении арматуры на упоры

P_m,t=P_m,0 - Δ P_t(t), (44) не должно быть большим, чем это установлено условиями

P_m,t  0,65·f_pk A_p , (45)

P_m,t  P₀  100A_p , (46)

где P_m,t , P₀ — в Н, A_p — в мм² .

P_m,t=357,03,31-34,66=322,37 кН< 0,65∙1200 509=397,02кН – условие выполняется,

P_m,t =322,37 кН< 840∙509  100·509=376,66 кН – условие выполняется.