4. Модуль зубчатого колеса.

Модуль зубчатого колеса, геометрический параметр зубчатых колёс. Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности d_д

к числу зубьев z или отношению шага t по делительной окружности к числу: m = d_д/z = ts/p. Для косозубых цилиндрических колёс различают: окружной модуль m_s = d_д/z= ts/p, нормальный модуль m_n = t_n/p, осевой модуль m_a = t_а/p, где t_s, t_n и t_a — соответственно окружной, нормальный и осевой шаги по делительному цилиндру. Значения Модуль зубчатого колеса стандартизованы, что является основой для стандартизации других параметров зубчатых колёс (геометрические размеры зубчатых колёс выбираются пропорционально модулю) и зуборезного инструмента

5. Качественные показатели работы зубчатого зацепления: коэффициент перекрытия, коэффициент удельного скольжения и давления.

Коэффициентом перекрытия eg называется величина отношения угла перекрытия зубчатого колеса к его угловому шагу, где под углом перекрытия понимают угол на который поворачивается колесо за время зацепления одной пары зубьев. Коэффициент перекрытия определяет величину зоны двухпарного контакта, когда одновременно зацепляются два последовательно расположенных зуба. Так как до окончания зацепления одной пары зубьев, следующая пара должна войти в контакт, нельзя допускать в прямозубых передачах  . Допустимое значение коэффициента перекрытия должно несколько превышать единицу и, в зависимости от назначения передачи и точности ее изготовления, выбирается в пределах  . Максимальное значение коэффициента перекрытия для зубчатых колес, обработанных инструментом со стандартным исходным производящим контуром, составляет 

Для характеристики влияния геометрической формы зуба на контактную прочность используется коэффициент удельного давления  . Из анализа формулы Герца, которая используется для оценки контактных напряжений в высшей паре, можно заключить, что единственный геометрический элемент в этой формуле - приведенный радиус кривизны 

где - радиусы кривизны профилей в контактной точке, знак + относится к внешнему зацеплению, - к внутреннему. Чтобы коэффициент давления характеризовал контактное напряжение не-зависимо от абсолютных размеров зуба, которые определяются модулем, введено понятие удельного давления как отношения модуля к приведенному радиусу кривизны

Коэффициент скольжения учитывает влияние геометрических и кинематических факторов на величину проскальзывания профилей в процессе зацепления. Наличие скольжения при одновременном нажатии одного профиля на другой приводит к износу профилей. Коэффициенты скольжения выражаются формулами:

;  , (50)

где vск –– скорость скольжения; vK1-K, vK2-K –– скорости перемещения точек контакта по профилям зубьев первого и второго колеса.

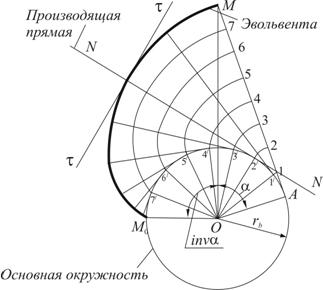
6. Эвольвента, ее характеристики и свойства.

Геометрическое место центров кривизны какой-либо кривой называется эволютой, а сама кривая по отношению к эволюте – разверткой или эвольвентой.. Эвольвента может быть получена как траектория точки прямой, перекатывающейся без скольжения по окружности.

В теории зацепления окружность, эвольвентой которой является профиль зуба, называется основной окружностью, ее диаметр обозначается - .

Тригонометрическая функция называется инволютой и обозначается , т.е. уравнение (4.4) может быть записано .

Характер и параметры зацепления определяются следующими свойствами эвольвенты:

1. Эвольвента не имеет точек внутри основной окружности и представляет собой спиральную кривую, начинающуюся от основной окружности;

2. Производящая прямая является одновременно касательной к основной окружности и нормалью к эвольвенте;

3. Радиус кривизны эвольвенты в любой точке равен длине касательной к основной окружности, проведенной из этой точки;

4. С увеличением радиуса основной окружности эвольвента становится более пологой и при обращается в прямую;

5. Длина отрезка нормали к эвольвенте (например ) равна длине дуги основной окружности (в данном случае );

Точка А основной окружности есть центр кривизны эвольвенты (в данном случае для точки М).