2.7. Взаимосвязь компонентов и результатов действий сложения и вычитания

В основе усвоения взаимосвязи между компонентами и резуль­татами сложения и вычитания лежит осознание учащимися пред­метного смысла этих действий. При этом следует учитывать, что особую трудность для некоторых детей представляет вычленение и удаление части множества, т. е. осознание тех предметных дей­ствий, которые связаны со смыслом вычитания.

В исследовании Г. Г. Микулиной¹ были выявлены интересные факты, которые необходимо учитывать при изучении смысла дей­ствия вычитания. Ею было установлено, что значительная часть учащихся при выполнении предметных действий, связанных с вы­читанием, фиксирует скорее пространственное отделение, разъе­динение двух множеств, чем вычленение и удаление части из це­лого. Такой вывод был получен на основе анализа результатов выполнения ряда заданий, предложенных ученикам. Приведем их.

1. Учитель берет бумажную полоску, говорит, что он сейчас с ней что-то сделает, и, обращаясь к ученику, просит внимательно следить за своими действиями, чтобы ответить на вопрос: «Какое действие я выполнил: сложение или вычитание?» Учитель отреза­ ет небольшую часть полоски и отодвигает ее в сторону. Большин­ ство учеников сразу отмечают, что выполнено вычитание. Учитель соглашается и записывает выражение 8-2, поясняя его следую­ щим образом: «Здесь записано, что мы из 8 см вычли 2 см. Пока­ жи, где 2 см полоски ... А теперь покажи, где 8 см».

Обычно учащиеся правильно показывают 2 см, но большинство первоклассников и даже третьеклассников относят 8 см не ко всей первоначальной длине полоски, а только к ее остатку.

2. На столе кубики (11 шт.). Учащимся это не сообщается. Учи­ тель говорит, что он сейчас произведет с ними действие и нужно определить, какое оно. Он отодвигает 3 кубика.

- Какое число вычитали? (3)

Учитель фиксирует это записью на доске □ - 3 и предлагает в «окошко» вписать нужное число кубиков. Многие ученики, посчитав

Микулина Г.Г. Действия с предметами как основа усвоения математиче­ских понятий,- «Начальная школа», 1983, № 9,

39

оставшиеся на столе кубики, записывают в «окошко» число 8 и вместо правильной записи 11-3 получается запись 8-3.

3. На столе кубики (12 шт.). Их число не сообщается учащимся. Учитель отодвигает 4 кубика и предлагает детям составить соот­ ветствующее выполненному действию выражение. В отличие от предыдущих в этом задании не дается никакой предварительной записи. Неверную запись 8-4 вместо 12-4 по-прежнему выпол­ няют многие ученики.

4. Школьникам выдаются карточки или кружки (больше 10), с помощью которых предлагается проиллюстрировать выражение 6-2. («Покажи на карточках это выражение».) И в этом случае не­ которые из них берут из стопки сначала 6 карточек, затем 2 и ото­ двигают эти 2 карточки от 6.

Происхождение описанных выше ошибок можно объяснить так. В психологии установлено, что дошкольникам свойственно не удерживать одновременно во внимании целое и его части: когда они оперируют частями, то уже не видят перед собой целого, и на­оборот. Преодоление этих ошибок происходит постепенно и обыч­но в возрасте 7-8 лет. Поэтому так важно продумать психологи­ческий аспект изучения этого вопроса.

Рассмотрим некоторые методические приемы, в которых учиты­ваются описанные выше психологические особенности младших

школьников.

1. Работая у доски с рисунками и дидактическими пособиями, полезно сначала предложить ученику показать предметные сово­купности, с которыми он действует, а затем уже назвать число предметов в них. Например, на доске 3 гриба, из них вычленяется и отодвигается 1. Ученикам предлагаются задания: «Покажи: а) сколько сначала было грибов; б) те грибы, которые отодвинули, и затем те, которые остались. При этом жест, указывающий на це­лое, должен быть особенным. (Он выполняется двумя руками и таким образом как бы объединяет пространственно разделенные при вычитании части.) Выполнение такого жеста (без упоминания числа предметов) позволяет быстро и наглядно прийти к нужному

обобщению.

2. Выполняя задания с рисунками, к которым дана запись вида D - □ = D, рекомендуется заполнять «окошки» не только в прямом порядке, но и начиная с любого. Например, после выяснения со­держания рисунка (изображены птички) учитель может спросить: «Какое число нужно записать после знака минус? После знака ра­венства? А теперь покажите на рисунке тех птичек, число которых нужно записать в первом "окошке"».

3. Можно использовать задания такого же рода, но со скрытыми количествами. При их выполнении внимание учащихся сосредота-

40

чивается на соотнесении элементов схемы и предметных совокуп­ностей. Например, на доске записана схема: D - D = D.

Учитель ставит на наборное полотно несколько карточек, сло­женных пачкой так, чтобы учащиеся не смогли их пересчитать. За­тем в соответствии со схемой он производит вычитание, сохранив оставшуюся часть карточек опять в виде пачки. Потом указывает в схеме «окошко»-вычитаемое и спрашивает, какое число нужно за­писать в него.

- Покажите те карточки, которые убрали. Пересчитайте их. Полученное число записывается во втором «окошке». Далее показываются, а потом подсчитываются карточки, число которых надо поставить в третьем «окошке», затем в первом. По­рядок обращения к «окошкам» нужно все время менять, а сами задания можно предлагать в игровой форме: «Если правильно по­кажешь, то можно сосчитать».

4. Так же можно использовать и другой методический прием. Например, из 6 карточек откладываются 2 и производится запись 6-2 = 4. Учитель обращает внимание на то, что в записи имеются три числа. Поэтому он предлагает трем ученикам взять карточки: одному - 6, другому - 2, третьему - 4. Учеников предупреждают, что это нужно сделать всем одновременно, по команде учителя. При выполнении задания обнаруживается, что все карточки либо забирает один ученик и тогда двум другим ничего не достается, либо двое забирают карточки, а одному ничего не достается. Нуж­но обязательно проиграть оба варианта распределения карточек, а в итоге подчеркнуть, что карточки каждого из двух ребят - это час­ти того, что должен взять третий. Заметим, что такое задание, да­же воспроизведенное несколько раз на нескольких уроках, вызы­вает у учащихся большой интерес.

5. Можно предлагать комплексное задание с карточками и со схемами. Например, на доске дана схема □ - п = П. Учитель про­делывает действие с пачками карточек так же, как в третьем слу­чае. Только теперь он уже указывает не на «окошки» в схеме, для которых учащиеся находили соответствующую группу карточек, а на карточки (например, оставшиеся) и предлагает найти для их числа место в схеме. Затем находится место для числа тех карто­чек, которые вычитали, и*запись принимает такой вид: D - 5 = 3. Учитель выражает удивление, обращая внимание учеников на то, что в схеме одно «окошко» осталось незаполненным, хотя карто­чек больше нет. Показывая жестом все целое, учащиеся называют учителю то значение, которого недостает.

Разрешение таких «противоречий» в игровой форме помогает детям усвоить взаимосвязь между компонентами и результатами действий сложения и вычитания. Однако, осознавая «предметную»

41

взаимосвязь компонентов и результатов действий, не все дети могут описать ее, пользуясь математической терминологией: сла­гаемые, значение суммы, уменьшаемое, вычитаемое, значение разности. В этом случае целесообразно использовать понятия це­лого и части и соотношение между ними (часть всегда меньше це­лого; если убрать одну часть, то останется другая).

Понятие целого и части позволяет как бы «материализовать» такие термины, как слагаемые, уменьшаемое, вычитаемое.

Например, устанавливая соответствие между рисунком и мате­матической записью:

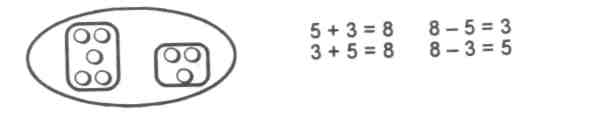
учащиеся рассматривают значение суммы как целое, а слагаемые - как его части. Отсюда: а) если из значения суммы вычесть одно слагаемое, то получим другое слагаемое; б) если к значению раз­ности (часть) прибавить вычитаемое (часть), то получим умень­шаемое; в) если из уменьшаемого (целое) вычесть значение раз­ности (часть), то получим вычитаемое (часть).

Ш Задание 17. Найдите в учебниках математики для начальных классов упражнения, в процессе выполнения которых учащиеся усваива­ют взаимосвязь между компонентами и результатами сложения и вычита­ния.