2.5. Число и цифра 0

Число нуль является характеристикой пустого множества, т. е. множества, не содержащего ни одного элемента. Для того, чтобы учащиеся представили себе такое множество, можно использовать различные методические приемы. Рассмотрим некоторые из них.

Один прием связан с установлением соответствия между чи­словой фигурой и цифрой, обозначающей количество предметов.

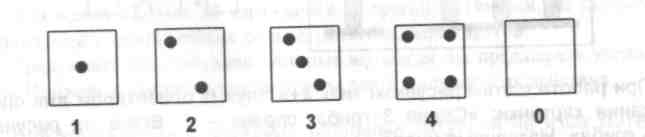
Этим подходом можно воспользоваться до изучения сложения и вычитания, на этапе формирования у учащихся представлений о

количественном числе.

Другой методический прием знакомит младших школьников с

нулем как результатом вычитания.

Для этой цели учащимся предлагаются предметные ситуации, которые они сначала описывают (рассказывают, что нарисовано на картинке), а затем записывают свой рассказ числовыми равенст­вами.

Например, в учебнике М1М дана серия картинок. На первом ри­сунке веточка, на которой три листочка. На втором рисунке на ве­точке два листочка, а на третьем - один. Дети комментируют рису­нок: «На веточке три листочка. Один листочек сорвали, осталось: 3-1 =2. Затем сорвали еще один листочек, осталось: 2-1 = 1. Еще один листочек сорвали, осталось: 1 - 1». Для записи полу­ченного результата в математике используется число: 1-1 = 0.

36

Следует иметь в виду, что при таком введении числа нуль у детей может сложиться неправильное представление о числе нуль как результате вычитания 1 - 1.

Чтобы этого не случилось, необходимо рассмотреть как можно больше различных ситуаций, связанных с получением числа нуль. В частности: на тарелке лежало 2 яблока. Нина и Таня съели их. Сколько яблок осталось на тарелке? Для записи 2-2 также ис­пользуется число нуль: 2-2 = 0. Аналогично 3-3 = 0, 4-4 = 0.

Можно предложить и такое задание: «Что изменилось?»

Дети обычно отвечают: «Ничего не изменилось».

- Может быть, кто-нибудь догадается, какую математическую запись можно использовать для этого случая,- говорит учитель. Обычно дети сами предлагают записать равенства: 5 + 0 = 5,5-0 = 5.

Для введения числа нуль можно придумать другие ситуации, связанные с изменением количества. Например, на фланелеграфе 3 зайца. Ученики закрывают глаза, учитель в это время изменяет количество зайцев (добавляя одного). Математическая запись вы­полненного предметного действия выглядит так: 3 + 1=4. Затем рассматриваются ситуации, соответствующие записям: 4 + 2 = 6, 6-2 = 4, 4 + 3 = 7ит. д. Наконец, дети закрывают глаза, но учи­тель оставляет картинку без изменения. Возникает вопрос - как записать такое «изменение» математическими знаками? Для этой цели можно использовать число нуль: 4 + 0 = 4,4-0 = 4.

II Задание 15. Найдите в учебнике Ml И страницу, на которой дети знакомятся с числом и цифрой 0. Какие методические приемы использо­ваны в учебнике?

37

2.6. Переместительное свойство сложения

Из курса математики вам известно, что для сложения целых неотрицательных чисел выполняются коммутативное и ассоциа­тивное свойства. В начальном курсе математики учащиеся знако­мятся с коммутативным свойством сложения, называя его «переместительное свойство сложения» или «перестановка сла­гаемых». Для его разъяснения могут быть использованы действия с предметными множествами, сравнение числовых равенств, в ко­торых переставлены слагаемые, сравнение суммы длин одинако­вых отрезков (полосок).

При формировании у детей представлений о смысле сложения полезно предлагать им такие ситуации для предметных действий, при выполнении которых они сами подмечают закономерность, связанную с переместительным свойством сложения. Например:

а) На левой тарелке 4 апельсина, на правой - 3. Покажи, сколь­ ко апельсинов на двух тарелках.

Ученики выполняют схематический рисунок и записывают ра­венство, подсчитав количество апельсинов на двух тарелках.

б) Теперь на левой тарелке 3 апельсина, на правой - 4. Покажи, сколько апельсинов на двух тарелках.

Ученики выполняют схематический рисунок и записывают ра­венство, подсчитав количество апельсинов на двух тарелках.

вы могли бы им предложить при изучении переместительного свойства сложения. Как вы думаете, с какой целью изучается переместительное свойство сложения в начальном курсе математики?