1 Бантова м.А., Бельтюкова г.В. Методика преподавания математики в начальных классах. - м., Просвещение, 1984, с. 234.

236

В этом случае целесообразно предложить им проблемное за­дание: «Боря идет до школы 10 минут, а Лена - 15. Подумайте, на какой вопрос вы можете ответить, а на какой нет:

• Кто тратит на дорогу времени больше (меньше)?

• Кто идет быстрее, а кто медленнее?»

В процессе обсуждения выясняется, что ответить можно только на первый вопрос. Для ответа на второй вопрос необходимо знать расстояние, которое проходят Боря и Лена.

Учитель дополняет условие: «Боря проходит расстояние 1 км, а Лена- 1500 м».

Важно, чтобы дети осознали обобщенную характеристику ско­рости как расстояния, пройденного за единицу времени, и в про­цессе решения задач использовали различные единицы скорости.

Так, в данном случае нужно 1 км выразить в метрах и после этого найти скорость Бори: 1000:10=100 (м/мин), а затем скорость Лены: 1500:15=100 (м/мин).

Получается, что Лена и Боря идут в школу с одинаковой скоро­стью.

Дальнейшая работа связана с анализом конкретных ситуаций и их наглядной интерпретацией.

Например:

Каждый час велосипедист проезжает 12 км, а пешеход прохо­дит 4 км.

За сколько времени велосипедист преодолеет данное расстоя­ние? За какое время преодолеет это расстояние пешеход?

Подготавливая детей к решению задач, связанных с движени­ем, необходимо повторить:

• единицы длины - 1 км, 1 м, 1 дм, 1 см, 1 мм;

• единицы времени - 1 ч, 1 мин, 1 с.

После этого познакомить с различными единицами скорости: 1 км/ч, 1 км/мин, 1 м/мин, 1 см/мин.

Так как задачи, связанные с движением,- это задачи с пропор- ' циональными величинами, внимание ребенка необходимо акцен­тировать на зависимости между величинами: скорость, время, рас­стояние. Для этой цели можно нарисовать три отрезка, в каждом из

237

Очень важно, чтобы дети не воспроизводили формально пра­вила, в которых находит отражение взаимосвязь величин: «чтобы узнать время, нужно расстояние разделить на скорость», «чтобы узнать расстояние, надо скорость умножить на время» и т. д. По­этому использование формул S=V«t; V=S:t; t=S:V на данном этапе нецелесообразно. Но при этом детям можно сказать, что скорость, время и расстояние условились обозначать специальными буква­ми.

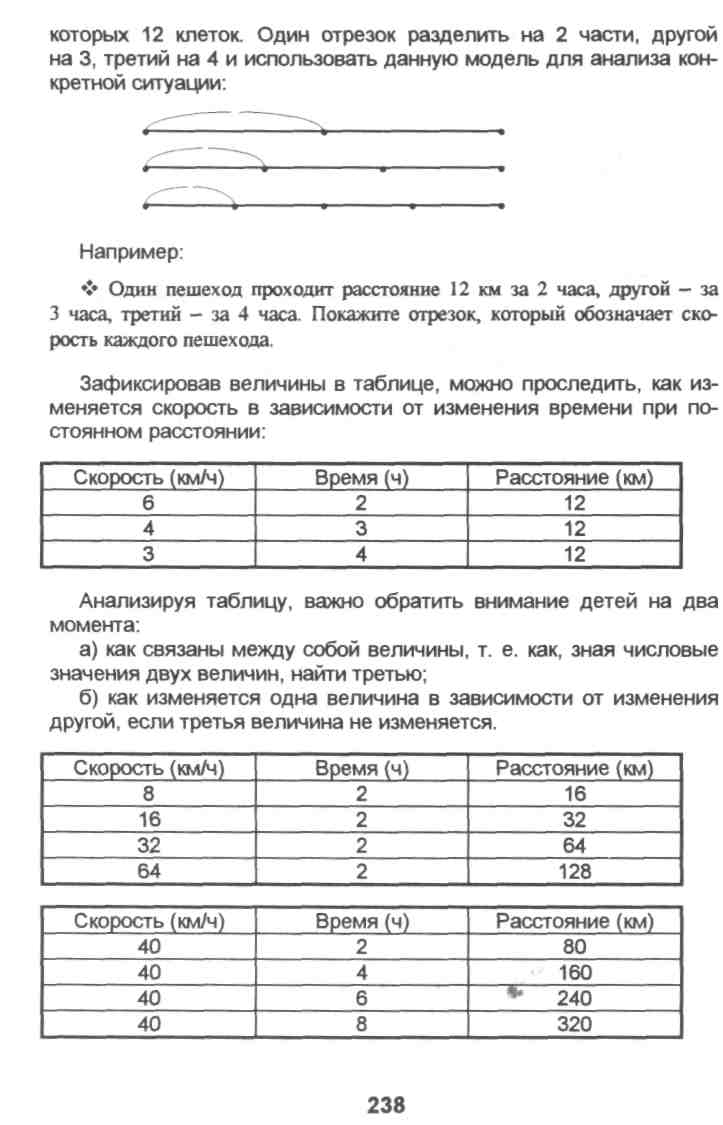
С первых уроков изучения данной темы, основной целью кото­рой является формирование у учащихся умения решать задачи с пропорциональными величинами скорость, время, расстояние, следует включать задания (задачи), требующие перевода одних единиц скорости в другие. Например:

♦ Скорость одного пешехода 50 м/мин, а другого - 4 км/ч. За какое время первый пешеход пройдет 12 км? За какое время это расстояние пройдет второй пешеход?

Выделив данные в задаче величины (расстояние, скорость) и искомую (время), необходимо обратить внимание на единицы, в которых выражена каждая величина.

В связи с тем, что расстояние выражено в километрах, единицы скорости необходимо преобразовать. Выполнение таких преобра­зований позволяет учащимся активно использовать ранее усвоен­ные знания и представления о пропорциональных величинах. А именно: если сказано, что за 1 мин пешеход проходит 50 м, то вы­разить данную величину в километрах младший школьник не мо­жет, поэтому он сначала выясняет, сколько метров пройдет пеше­ход за 1час. Так как 1 ч - это 60 мин, а за 1 мин пешеход проходит 50 м, значит, за 60 мин он пройдет расстояние в 60 раз больше: 50.60=3000 (м).

Имеем скорость 3000 м/ч. Теперь можно расстояние выразить в километрах: 3000 м = 3 км. Получаем: 50 м/мин = 3 км/ч.

Для формирования у учащихся представлений о скорости по­лезно предлагать задачи, в которых для ответа на вопрос не нужно выполнять вычислений:

♦ Мальчики соревновались в беге на 100 м. Коля пробежал дистан­ цию за 16 с, Боря - за 15 с, а Вова - за 18 с. Кто бежал с большей скоро­ стью?

♦ Таня и Лена живут на одной улице. Они одновременно выходят в школу:

239

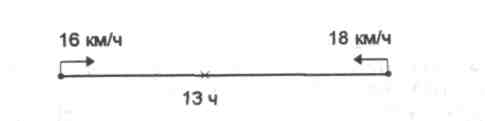
Помимо схем, целесообразно при решении задач на движение использовать различные сочетания методических приемов: срав­нения, выбора, преобразования, конструирования.

Рассмотрим, как можно организовать деятельность учащихся, работая на уроке с приведенной выше задачей.

1-й вариант

В учебнике текст задачи и готовая схема.

Учитель предлагает самостоятельно прочитать задачу, рас­смотреть схему и записать ее решение по действиям.

Предположим, что большая часть детей не приступила к реше­нию задачи. В этом случае учитель предлагает учащимся прочи­тать текст задачи, который записан на доске: «Два велосипедиста одновременно выехали навстречу друг другу и встретились через три часа. Какое расстояние было между ними первоначально, если один ехал со скоростью 16 км/ч, а другой - 18 км/ч?»

• Сравните тексты задач. В чем их сходство и в чем различие? (В условии первой задачи сказано, что велосипедисты выехали в 10 часов, а во второй задаче это заменили словом «одновремен­но»; в первой задаче нужно узнать, через сколько часов они встре­тились, а во второй это известно и т. д.)

• Но ведь во второй задаче не сказано, что каждый велосипе­дист был в пути 3 часа, а сказано так: через 3 часа они встрети­лись. (Если они выехали одновременно и встретились через три часа, то это значит, что каждый был в пути три часа.)

• А какой велосипедист пройдет до встречи большее расстоя­ние? (Тот, у которого скорость больше.)

• Прочитайте еще раз внимательно первую задачу и запишите ее решение.

Учитель дает учащимся время для самостоятельной работы. После этого он предлагает учащимся обсудить различные спо­ собы решения данной задачи. При этом можно сказать, что эти способы решения он обнаружил в тетрадях у некоторых детей: а) 1) 13 - 10=3 (ч) б) 1)18 - 16=2 (км/ч)

2) 18+16=34 (км/ч) 2)16«6=96 (км)

3)34«3=102 (км) 3)2*3=6 (км)

4) 96+6=102 (км)

241

- А теперь прочитайте другую задачу, ту, которая написана на доске. Чем эта задача отличается от той, которая дана в учебнике? На доске текст: «Два велосипедиста одновременно выехали на­встречу друг другу и встретились через 3 часа. Какое расстояние было между ними через 2 часа, если один ехал со скоростью 16 км/ч, а скорость другого была на 2 км/ч больше?»

Учащиеся обсуждают внесенные в условие изменения и срав­нивают задачу с той, которая в учебнике.

- Подумайте, какие действия нужно выполнить в этой задаче, чтобы ответить на поставленный вопрос, и запишите самостоя­тельно её решение.

2-й вариант

Предлагается сначала задача с недостающими данными.

♦♦• Два велосипедиста выехали навстречу друг другу и встретились в 13 часов. Сколько времени был в пути каждый велосипедист? Какое рас­стояние было между ними первоначально, если один велосипедист ехал со скоростью 16 км/ч?

Текст обсуждается фронтально. Учащиеся выдвигают свои предложения о решении задачи. Обнаруживают, что в задаче не хватает данных, и обосновывают свое мнение. Дополняют условие задачи. После этого решают самостоятельно сконструированную ими задачу. Затем целесообразно обсудить другие способы реше­ния, как это сделано в первом варианте.

Ш Задание 114. Придумайте свой вариант работы с данной за­дачей, используя приемы: выбор схемы, условие с лишними данными, постановка вопроса к данному условию.

Ш Задание 115. Найдите в учебниках математики для началь­ных классов или придумайте сами задачи с величинами «скорость», «время», «расстояние», на нахождение четвертого пропорционального, на пропорциональное деление, на нахождение неизвестного по двум разно­стям. Опишите возможные варианты работы с этими задачами.