4.4. Организация деятельности учащихся при

обучении решению задач

с пропорциональными величинами

Особую сложность для младших школьников представляют за­дачи с пропорциональными величинами. Одна из причин возни­кающих у детей трудностей в процессе решения этих задач заклю­чается в том, что понятие «пропорциональная зависимость» не является предметом специального изучения и усвоения.

«Связи между пропорциональными величинами раскрываются с по­мощью решения простых задач на нахождение одной из величин по дан­ным, соответствующим значениям двух других величин (например, зада­ча на нахождение стоимости по известным цене и количеству)»

Поэтому при решении простых задач с пропорциональными ве­личинами целесообразно использовать как уже рассмотренные методические приемы обучения решению задач, так и те приемы, которые способствуют формированию у учащихся представлений

0 пропорциональной зависимости величин.

В числе этих приемов можно назвать: а) изменение одного из данных задачи;

¹ Бантова М.А., Бельтюкова Г.В. Методика преподавания математики в

начальных классах. - М., Просвещение, 1984, с. 227.

226

б) сравнение результатов решения задач, в которых изменяется одно из данных;

в) интерпретация задачи в виде схемы, запись задачи в табли­ це;

г) анализ текстов задач с недостающими и лишними данными.

Например, учащимся можно предложить задачи с недостающи­ми данными, при анализе которых они, пользуясь житейскими представлениями, сами употребляют термин «зависит».

• Миша купил на 10000 р. кисточки и на 5000 р. карандаши. Чего Миша купил больше: карандашей или кисточек?

• Маша купила 5 тетрадей в клетку и 2 блокнота. За что она заплати­ла денег больше, за тетради или за блокноты?

Анализируя тексты этих задач, учащиеся обнаруживают, что в них не хватает данных и что ответы на вопросы, поставленные в задачах, зависят от цены предметов. Учащиеся отвечают: «Это зависит от того, сколько стоит 1 блокнот, 1 тетрадь» и т. д. Для разъяснения учащимся математического смысла понятия «зависит» необходимо проследить, как изменяется одна величина в зависимости от изменения другой при постоянной третьей. Для этой цели можно воспользоваться приведенными задачами, до­полнив их условие, или рассмотреть, например, простую задачу с недостающими данными:

♦ В палатку привезли 6 ящиков апельсинов. Сколько килограммов апельсинов привезли в палатку?

Учащиеся быстро обнаруживают, что ответить на вопрос задачи нельзя, так как неизвестна масса одного ящика. Выделенные ве­личины полезно зафиксировать в таблице:

Дети дополняют условие и решают задачу. Затем надо просле­дить, как будет изменяться общая масса в зависимости от измене­ния массы одного ящика при постоянном их количестве или в за­висимости от изменения количества ящиков при постоянной массе

Традиционно сложилось так, что задачи с пропорциональными величинами, связанные с движением тел, выделяются в специ­альную тему: «Скорость. Время. Расстояние».

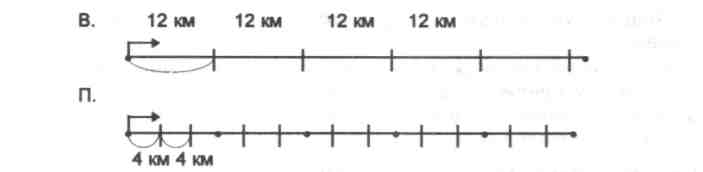
Специфика этих задач обусловливается введением такой ве­личины, как скорость движения, а также использованием при их решении схем, которые отражают не отношения между величина­ми, а процесс движения.

Опираясь на опыт ребенка при разъяснении понятия скорость движения, следует иметь в виду, что употребляя в своей речи сло­ва «быстрее» и «медленнее», дети связывают их смысл с такой величиной, как время. Поэтому знакомство с понятием «скорость движения» можно начать с вопроса: «Как вы понимаете такую фразу: автомобилист едет быстрее, чем велосипедист; пешеход идет медленнее, чем лыжник?»

Возможно, отвечая на этот вопрос, некоторые дети используют понятие «скорость», но, разъясняя его смысл, они так или иначе обратятся к словам: быстрее - медленнее. (У одного скорость больше - он идет быстрее, у другого меньше - он идет медлен­нее.) В этом случае следует обсудить, что значит быстрее и мед­леннее. Дети обычно объясняют это так: быстрее, значит, меньше времени; медленнее, значит, больше времени.

■