2.25. Алгоритм письменного деления

Из курса математики вам известно, что письменное деление рассматривается как действие деления с остатком. Поэтому созна­тельное овладение алгоритмом письменного деления во многом зависит от умения находить остаток при делении одного числа на другое. Основа этого умения - осознание взаимосвязи между де­лимым, делителем, неполным частным и остатком, которая нахо­дит выражение в равенствах: a=b-q+r, r=a - tog, где а - делимое, to - делитель, q - неполное частное, г- остаток.

Как было ранее сказано (см. п. «Деление с остатком»), эта связь лучше осознается детьми в том случае, когда они выполняют де­ление с остатком, используя способ подбора, позволяющий скон­центрировать внимание на взаимосвязи умножения и деления, на способе нахождения остатка и на том, что остаток должен быть меньше делителя.

Помимо деления с остатком как одной из основных операций письменного деления, для успешного овладения алгоритмом уче­ники должны усвоить разрядный и десятичный состав числа, взаи­мосвязь умножения и деления.

Формирование у младших школьников навыков письменного деления зависит не только от усвоения ими математических поня-

5* 131

тий и способов действий, лежащих в основе алгоритма, но и от то­го, как будет построен процесс изучения нового способа действия.

В учебнике МЗМ нашел отражение подход, при котором дети овладевают алгоритмом письменного деления, рассматривая по­следовательно различные частные случаи деления чисел. Напри­мер, при делении на однозначное число сначала рассматривается случай, когда первое неполное делимое выражается однозначным числом, обозначающим количество сотен: 794:2, 984:4, 985:5, 681:3, затем отрабатывается умение делить числа для случая, ко­гда первое неполное делимое - двузначное число, обозначающее количество десятков (376:4) или сотен (1984:8).

Затем отрабатывается умение делить числа для случаев, когда в частном отсутствуют единицы какого-либо разряда: 4680:3, 432:4. После этого - случай деления с остатком, затем - случай деления чисел, оканчивающихся нулями: 5130:90, 2580:30, 46800:600, 37600:400.

Отдельно отрабатывается умение делить на двузначные и трехзначные числа. При этом сначала рассматривается случай, когда в частном получается однозначное число; затем, когда в ча­стном получается двузначное число; затем случай деления на двузначное число с остатком; затем деление на двузначное число, когда в частном получается трехзначное число, в котором отсутст­вуют единицы одного разряда. При делении на трехзначное число сначала рассматривается случай, когда в частном получается од­нозначное число, затем, когда в частном двузначное число.

Таким образом, при данном подходе выделяются 12 частных случаев, каждый из которых рассматривается по определенному плану:

1. комментируется (объясняется) образец записи деления;

2. пользуясь данным образцом, учащиеся решают аналогичные примеры (закрепляют данный случай деления);

3. выполняются упражнения, включающие решение примеров как нового случая деления, так и ранее рассмотренных.

Ш Задание 67. Познакомьтесь с последовательностью рассмотре­ния случаев деления в учебнике МЗМ. К каким записям деления дан под­робный комментарий, к каким - краткий, какие записи деления учащиеся должны объяснить сами? Конкретизируйте пункты плана для каждого случая деления упражнениями, предлагаемыми в учебнике.

Рассмотрим другой подход к изучению деления многозначных чисел, целью которого является усвоение общего способа дейст­вий и формирование умения самостоятельно и осознанно исполь­зовать его в различных частных случаях.

132

Этот подход нашел отражение в учебнике МЗИ.

Следует иметь в виду, что возможность такого подхода нельзя рассматривать только в рамках одной темы. Она (возможность) определяется целями и ложкой построения всего курса, в процес­се которого у учащихся целенаправленно формируются умения анализировать, сравнивать, обобщать.

Следует также иметь в виду, что изучению деления многознач­ных чисел при этом подходе предшествует тема «Деление с остат­ком», в процессе работы над которой учащиеся знакомятся с запи­сью деления «уголком» и с механизмом подбора цифры в частном (см. п. 2.22.«Деление с остатком»). Кроме того, теме «Деление с остатком» предшествует изучение алгоритма письменного умно­жения на однозначное число.

Основная задача подготовительной работы (будем рассматри­вать первый этап изучения темы как подготовку к знакомству с алгоритмом письменного деления) в учебнике МЗИ, так же как и в учебнике МЗМ, связана с актуализацией знаний, умений и навыков, т. е. с повторением ранее изученных вопросов, усвоение которых необходимо для осознанного восприятия алгоритма.

В число этих вопросов входят: взаимосвязь умножения и деле­ния, деление с остатком, свойство деления суммы на число и его использование для выполнения устных вычислений.

Решение этой задачи может осуществляться по-разному, в за­висимости, как уже было сказано, от целей курса и ложки его по­строения. Эти различия находят отражение в учебных заданиях.

И Задание 68. Сравните задания, предложенные в учебниках МЗМ и МЗИ на подготовительном этапе к знакомству с алгоритмом письменного деления. В чем их различие? Опишите деятельность учащих­ся при выполнении этих заданий.

Учебник МЗМ.

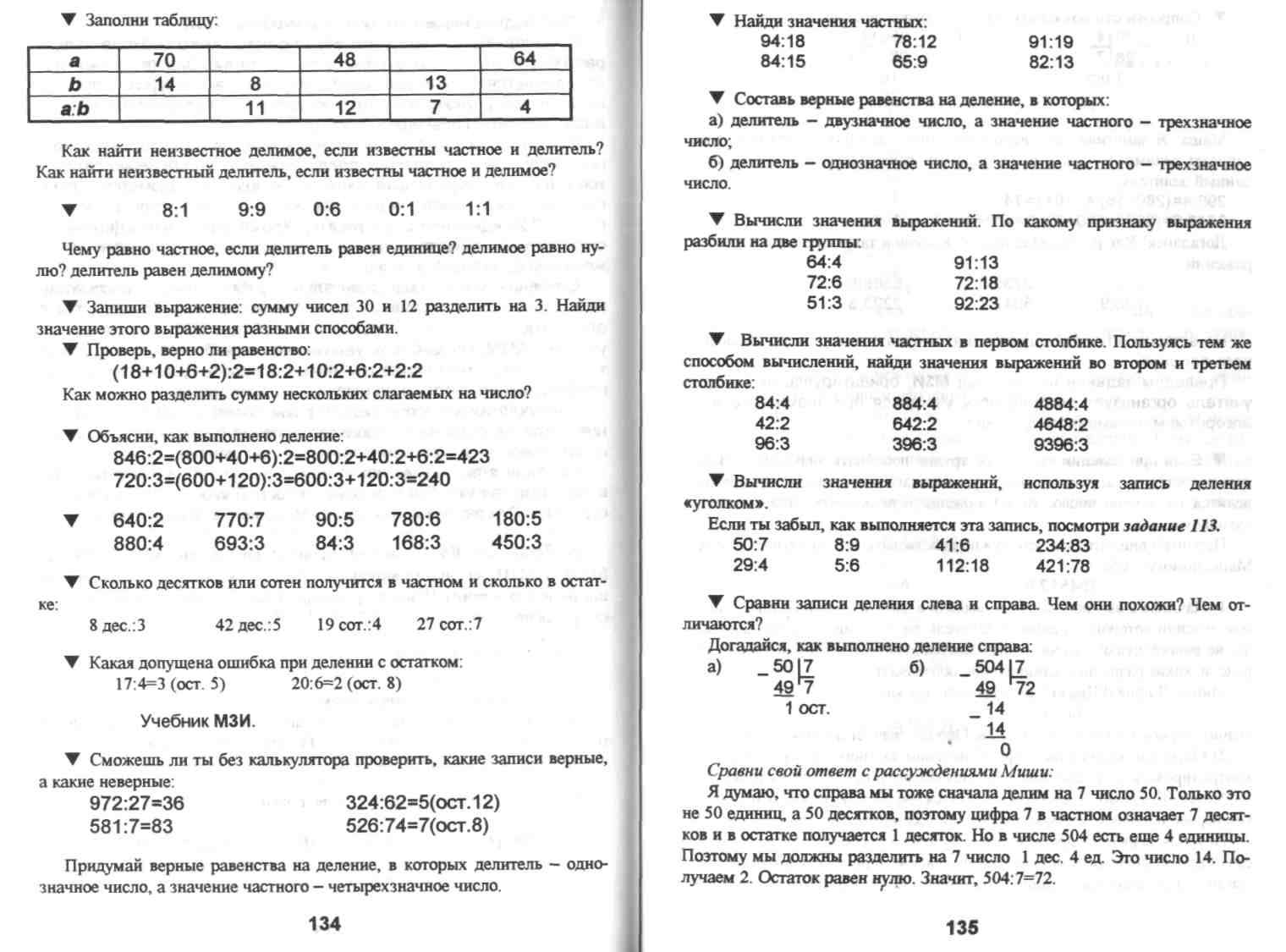
▼ Деление связано с умножением.

Разделить 48 на 12 - значит, найти такое число, при умножении на ко­торое делителя 12 получится делимое 48. Это число 4. Значит, 48:12=4. Что значит: разделить 72 на 9; 100 на 25?

Т Проверь с помощью умножения, правильно ли выполнено деление: 95:19=5 180:6=30 450:3=150

133

3. формальным введением единиц величин и соотношений ме­жду ними (см. этапы формирования представлений о величинах, п. 2.10.);

4. однообразием упражнений, связанных с переводом однород­ных величин одних наименований в другие.

Ш Задание 70. Проанализируйте учебники М1М и М1И и ответь­те на вопросы:

а) Как вы понимаете «формальное введение единиц величин»?

б) Какая работа проводится в одном и другом учебнике по формиро­ ванию у учащихся представлений об измерении длины?

в) Какие упражнения предлагаются в одном и другом учебнике для усвоения соотношений между единицами длины? (Выпишите все упраж­ нения.)

г) Какими упражнениями на соотношение единиц длины следует до­ полнить, по вашему мнению, один и другой учебник?

Ш Задание 71. Проанализируйте учебники М2М и М2И и ответь­те на вопросы:

а) С какими величинами и единицами их измерения знакомятся уча­ щиеся второго класса в одном и другом учебнике?

б) С какими единицами длины знакомятся учащиеся во втором классе?

в) Какими упражнениями на соотношение единиц величин нужно, по вашему мнению, дополнить один и другой учебник?

В третьем классе обобщаются знания о соотношении единиц величин и дети учатся выполнять действия с величинами, выра­женными в единицах двух наименований. Эта работа может быть организована по-разному.

В учебнике МЗМ последовательно рассматриваются сначала единицы длины, затем единицы массы, единицы времени, а дей­ствия с величинами учащиеся выполняют при изучении письмен­ного сложения и вычитания, умножения и деления.

Для усвоения соотношений между единицами длины предлага­ются упражнения:

• на измерение;

• на построение отрезков определенной длины, выраженной в единицах двух наименований;

• на перевод величин, выраженных в одних единицах, в другие единицы измерения;

• на сравнение однородных величин, выраженных в единицах различных наименований.

Аналогичные задания предлагаются при изучении тем «Единицы массы», «Единицы времени».

Ш Задание 72. Найдите в учебнике МЗМ задания указанных ви­дов, которые выполняются при изучении единиц длины, массы, времени. Составьте учебные задания данных видов с различными величинами.

К выполнению действий с величинами учащиеся приступают после того, как рассмотрен предлагаемый им образец. Например:

Т Объясни, как выполнено сложение: 3 т 500 кг + 300 кг = 3 т 800 кг

3 т 500 кг + 1 т = 4 т 500 кг

;

Т Реши с объяснением:

7 км 300 м + 600 м 25 м 40 см + 30 м

7 км 300 м + 5 км 25 м 40 см + 30 см

▼ Объясни, как выполнено вычитание:

4 км 700 м - 400 м = 4 км 300 м

7 км — 4 км 700 м = 2 км 300 м 4 км 300 м - 2 км 300 м = 2 км

▼ Реши с объяснением:

3 кг 900 г - 700 г 3 м - 25 см

3 кг — 1 кг 200 г 6м-1м6дм

▼ Объясни, как выполнено сложение и вычитание: 42 м 65 см + 26 м 83 см = 69 м 48 см

4265

^Т2683

6948

8 т 204 кг - 3 т 657 кг = 4 т 547 кг

_8204 3657 4547

▼ Реши с объяснением: 8 км 645 м + 4 км 460 м 8ц 36 кг—5ц 48 кг

При изучении темы «Площадь фигуры» учащиеся знакомятся с единицами площади: 1 см², 1 дм², 1 м² и с соотношениями между ними:

142

143

1 м² = 100 дм² 1дм² = 100 см² 1 м² = 10000 см²

Ш Задание 73. Найдите в учебнике МЗМ задания, в процессе вы­полнения которых учащиеся усваивают соотношения единиц площади.

Ш Задание 74. Проанализируйте задачи, предлагаемые в учебнике МЗМ. Найдите задачи, в которых даны величины, выраженные в едини­цах различных наименований. Приведите рассуждения учащихся при пе­реводе величин, выраженных в одних единицах измерения, в другие.

В учебник МЗИ для обобщения знаний о соотношении единиц величин и для выполнения действий с ними введена тема «Действия с величинами».

Одной из задач темы является формирование умения перево­дить однородные величины, выраженные в единицах одних на­именований, в другие единицы.

Для этого прежде всего необходимо, чтобы учащиеся знали, какими единицами нужно пользоваться при измерении каждой ве­личины.

С этой целью им предлагаются задания:

Т На какие группы можно разбить единицы величин:

а) 1 ч, 1 т, 1 мин, 1 с, 1 ц, 1 кг

б) 1 м², 1 дм, 1 км, 1 см², 1 мм, 1 т, 1 кг

▼ Какая величина «лишняя»? .

а) 3080 см, 5407 км, 6027 дм, 4078 кг, 18009 м

б) 120 см, 12 дм, 1 м 2 дм, 1 м 20 см, 1 м 2 см

Выполняя это задание, в строке а) учащиеся соотносят едини­цы измерения с определенной величиной и называют в качестве «лишней» - 4078 кг (масса).

Работу с заданием можно продолжить, выразив, например, ка­ждую величину в единицах других наименований: 3080 см = 30 м 80 см. Учащиеся могут обосновать свои действия, так как такие вопросы, как смысл деления, деление с остатком, десятичный .со­став числа, уже изучены. Ответ ученика в данном случае может выглядеть так: 1 м = 100 см. Узнаем, сколько раз в 3080 см содер­жится по 100 см, т. е. узнаем, сколько сотен содержится в числе 3080 (30 сотен). Ответив на этот вопрос, мы узнаем, сколько в 3080 см содержится метров (30 м и еще 80 см).

144 |

Можно воспользоваться и алгоритмом письменного деления:

_ 30801100

300 ПИТ

80 ост.

Далее: 10 см = 1 д_м, 80 см = 8 дм, 3080 см = 30 м 8 дм. Работая с этим же заданием, можно найти, например, сумму двух величин: 3080 см + 6027 дм. Для этого нужно выразить вели­чины в единицах одного наименования:

1) 3080 см = 308 дм 2) 6027 дм = 60270 см

,6027 , 3080

"*" 308 ~^Г60270

6335 63350

6335 дм = 633 м 5 дм 63350 см = 633 м 50 см

При нахождении «лишней» величины в строке б) следует искать другой признак - числовое значение величин. Для этого нужно все величины выразить в единицах одного наименования: 12дм = 120 см 1 м 2дм = 12дм = 120 см

1м 20 см = 120 см 1м2см = 102см

Усвоению соотношения единиц величин способствуют такие задания:

▼ Запиши величины в порядке возрастания:

5085 дм, 5085 см, 5085 км, 5085 м

▼ По какому признаку записаны величины в каждом столбике:

74 м 8 т

740 дм 80 ц

7400 см 8000 кг

74000 мм 8000000 г

Составь по этому правилу столбики для величин. 9 км, 1 сут, 6 м²

Т По какому правилу составлена первая строка таблицы? Пользуясь этим правилом, вставь пропущенные числовые значения величин.

▼ Найди закономерность и продолжи каждый ряд:

а) 93 см, 8 дм 6 см, 79 см, 7 дм 2 см, 65 см ...

б) 2 м 8 дм, Змб дм, 4 м 4 дм, 5 м 2 дм...

Выполняя данное задание, учащиеся сначала находят разность между первой и второй величиной ряда:

93 см-8 дм 6 см; 8 дм 6 см = 86 см;

93 см - 86 см = 7 см

Проверяется, в каком отношении находятся вторая и третья ве­личины в ряду:

86 см - 7 см = 79 см;

79 см + 7 см = 86 см = 8 дм 6 см и т. д.

Продолжаем ряд: 65 см - 7 см = 58 см.

В соответствии с правилом записи ряда эта величина записы­вается так: 5 дм 8 см.

Далее: 5дм8см-7см = 5дм1см = 51см; 5дм1см-7см = 4дм4см; 4 дм 4 см - 7 см = 3 дм 7 см = 37 см ...

▼ Дополни каждую величину до 3 км:

1781м 2503 м

2073 м 2909 м

Т Вставь пропущенные числа, чтобы получились верные равенства: 7 дм 2 см + 4 см = ... см 7т2ц + 4ц=...ц 18 мин- 15 с= . . . мин ... с 12 км 600 м - 600 м = D км П м

Важно, чтобы учащиеся понимали, что складывать, вычитать и сравнивать можно только однородные величины. Для этой цели предлагаются задания.

▼ Подумай! Какие величины можно сложить? Вычисли их сумму: 3084 м + 285 дм 813 м² + 545 дм²

840 м + 120 м² 703 дм + 102 кг

2м6дм4см + 6см Зм7дм5мм + 3мм

При выполнении задания полезно обсуждать два способа qno-жения величин, один из которых связан с переводом их в единицы одинаковых наименований, другой - когда эту операцию можно не выполнять:

2м6дм4см + 6см = 2м7дм

4 см + 6 см = 10 см

10 см + 1 дм = 2 дм

2 м 6 дм +1 дм= 2 м 7 дм

Т Подумай! Какие величины можно сравнивать? Поставь знаки < или >:

7300 мм ... 73 км 54 км ... 52 кг

35 м... 32 м² 20 км... 207 м

Не менее важно, чтобы учащиеся могли осознанно использо­вать различные единицы величин для практических измерений.

Догадайся! Какими единицами пользовались при измерении? За-пропуски.

а) Расстояние между городами 760 ...

б) Высота полета самолета 12300 ...

в) Площадь участка 420 ...

г) Масса курицы 4 ...

д) Высота дома 51 ...

е) Ширина стола 1...

ж) Рост человека 160 ...

И Задание 75. Подберите из учебника или составьте сами различ­ные задания, в процессе выполнения которых учащиеся усваивают соот­ношения между единицами массы (времени) и учатся складывать эти ве­личины.

Сравните задания в учебниках МЗМ и МЗИ. В чем их различие?