1 Бантова м.А. Бельтюкова г.В. Методика преподавания математики в начальных классах. - м., Просвещение, 1984, с. 77.

66

ID Задание 37. Ориентируясь на виды приведенных заданий, со­ставьте сами различные учебные задания, в процессе выполнения которых учащиеся будут усваивать смысл умножения.

II Задание 38. Найдите в учебнике М2М страницы с записями: 0 • □ и 1«D. Нужно ли специально выделять умножение нуля и единицы на число? Могут ли ученики найти произведение этих чисел, пользуясь опре­делением умножения?

Смысл умножения тесно связан с понятием «увеличить в не­сколько раз». Поэтому важно разъяснить детям, что запись 2*5 можно прочитать: «2 повторить 5 раз», «по 2 взять 5 раз», «2 ум­ножить на 5» и «2 увеличить в 5 раз».

Тем не менее, в различных учебниках математики этот вопрос решается по-разному.

В учебнике М2М вводятся понятия «больше в» и «меньше в» одновременно. Естественно, это можно сделать только после того, как дети познакомятся с делением. В связи с этим работа над ус­воением смысла умножения и понятием «больше в» значительно разведена во времени. Для введения понятий «больше в», «меньше в» в учебнике используется комментирование рисунков. На одном изображены зеленые квадраты и синие круги.

К рисунку дано пояснение: «Квадратов 3. Синих кружков 4 раза по 3. Кружков в 4 раза больше, чем квадратов, а квадратов в 4 раза меньше, чем кружков».

Ориентируясь на данные образцы, учащиеся выполняют такое задание:

Т Сделай по задаче рисунок и реши задачу: «Для детей детского сада купили 4 зеленых мяча, а красных в 3 раза больше, чем зеленых. Сколько красных мячей купили детям?»

Так как в учебнике реализуется подход, при котором простая задача является средством формирования понятий, то последую­щая работа по усвоению понятий «больше в», «меньше в» связана с решением простых задач на предметном уровне. Для того, чтобы дети не путали понятия «больше в» и «меньше в», им предлагают­ся задания вида:

«Сделай по задаче рисунок и реши задачу».

73

2.14. Переместительное свойство умножения

В курсе математики начальных классов нашли отражение все свойства умножения: коммутативное, ассоциативное и дистрибу­тивное.

Коммутативность умножения представлена в учебниках как пе­реместительное свойство: от перестановки множителей значение произведения не изменяется. При знакомстве с этим свойством умножения учащиеся выполняют задания на соотнесение рисунка с математической записью и на сравнение числовых выражений, в которых переставлены множители. Усвоение формулировки пере-местительного свойства умножения обычно не вызывает затрудне­ний, хотя многие дети и ошибаются, называя множители слагае­мыми, а произведение - суммой. Это объясняется не только тем, что они не усвоили названий компонентов и результатов действий умножения и сложения, но и является следствием формального подхода к изучению самого переместительного свойства, когда дети абстрагируются от конкретных ситуаций, связанных со смыс­лом умножения.

Следствием формального подхода к изучению данного свойст­ва является и то, что многие учащиеся путают, что означают пер­вый и второй множители в записи произведения. Чтобы предупре­дить эту ошибку, полезно предлагать им упражнения на выполне­ние рисунков, соответствующих той или иной конкретной ситуации. Например: «На каждую тарелку положили по 2 яблока. Покажи, сколько яблок на шести тарелках». Большинство детей выложат на фланелеграфе такой рисунок:

и выполнят запись 2*6=12. Стоит сразу же выяснить, можно ли к данному рисунку выполнить такую запись: 6*2=12? При обсужде­нии предлагается заменить произведение суммой и найти резуль­тат. Выясняется, что означают в данном случае числа 6, 2 и 12. Делается вывод, что 6*2 к данной ситуации не подходит. Учитель предлагает иначе разложить яблоки на тарелки, в соответствии с записью 6*2=12. Отсюда делается вывод, что переместительное свойство умножения справедливо только для числовых выражений (3*4=4*3, 5*8=8*5). Если же речь идет о предметной ситуации, то необходимо учитывать, что обозначает каждое число в записи произведения.

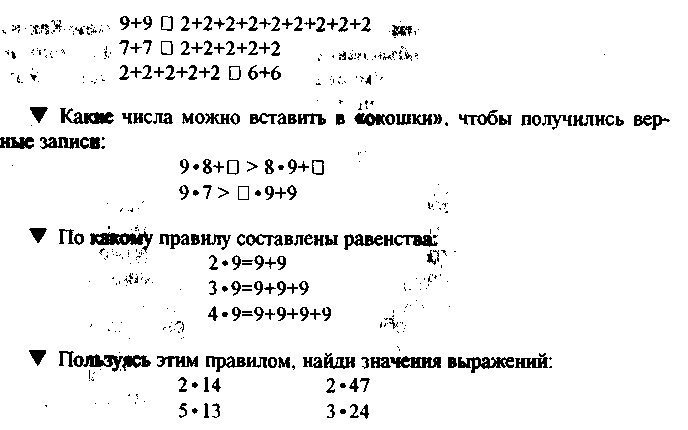
Выполнение таких упражнений оказывается полезным в даль­нейшем при решении текстовых задач на умножение, в которых даны не отвлеченные числа, а числовые значения величин. Сле­довательно, при перестановке множителей произведение может не иметь смысла, соответствующего сюжету задачи.

Рассмотрим, например, такую задачу: «От мотка проволоки длиной 82 м отрезали 4 куска, по 8 м каждый. Сколько метров про­волоки осталось в мотке?» Приведем два варианта записи реше­ния:

1-й вариант га 2-й вариант

1. 8*4=32 (м) 1) 4*8=32 (м)

2. 82 - 32=50 (м) 2) 82 - 32=50 (м)

В практике начального обучения традиционно второй вариант записи решения задачи считается выполненным с ошибкой. Это объясняется тем, что, комментируя решение задачи, дети (да и сам учитель) делают это так: «Я 8 метров умножу на 4, т. е. повто­рю 8 метров 4 раза». Если так же прочитать запись, которая дана справа, а именно: «Я 4 куска умножу на 8», то, конечно, это не имеет смысла.

Но если в записи решения наименования даны только в скоб­ках, то обе записи первого действия можно считать верными, т. к. предметный смысл произведения находит отражение в том наиме­новании, которое записано в скобках, а умножение выполняется с числами.

Знакомство с переместительным свойством умножения позво­ляет предлагать учащимся задания, при выполнении которых они используют не только определение умножения, но и его перемес­тительное свойство. Например:

▼ Можно ли, не вычисляя значений выражений, вставить в «окошки» знаки <, >, =, чтобы получились верные записи:

76

Ш Задание 40. Найдите в различных учебниках математики для на­чальных классов страницы, где учащиеся знакомятся с переместительным свойством умножения. Придумайте задания, при выполнении которых нужно использовать определение умножения и его переместительное свойство.

II Задание 41. Найдите в учебнике М2М страницы, которые связа­ны с изучением случаев умножения на 1 и на 0. Затем рассмотрите два варианта объяснения темы «Умножение на 1».

1) Один учитель предложил:

а) сначала найти значение выражения 1*5,

б) переставить множители и найти результат, применяя перемести­ тельное свойство умножения: 1x5=5x1.

Далее делается вывод: при умножении числа на единицу получаем то число, которое умножаем.

2) Другой учитель представил случай умножения числа на 1 как осо­ бый, когда нельзя заменить произведение суммой и найти результат; нуж­ но запомнить, что при умножении любого числа на 1 получаем то число, которое умножаем. Затем он предложил ученикам самостоятельно найти значения произведений 1x6; 1x7 и сравнить равенства в каждой паре:

6*1=6 7*1=7 12*1=12

1*6=6 1*7=7 1*12=12

В результате был сделан вывод о том, что для случая умножения с едини­цей выполняется переместительное свойство умножения.

77

Какое объяснение вы считаете правильным? Обоснуйте ответ. Как вы думаете, будет ли зависеть объяснение случая умножения на 1 от того, на каком этапе изучения темы «Умножение» он рассматривается? Проду­майте объяснение случая умножения на нуль.