2.11. Таблица сложения однозначных чисел (с переходом через десяток)

Усвоение нумерации двузначных чисел, таблицы сложения (в пределах 10) и соответствующих ей случаев вычитания позво­ляет организовать с учащимися работу по усвоению таблицы сло­жения однозначных чисел (с переходом через десяток) и соответ­ствующих ей случаев вычитания.

В начальном обучении математике прием сложения однознач­ных чисел с переходом через десяток включает следующие опе­рации:

а) первая операция связана с дополнением большего слагаемо­ го до числа 10;

б) вторая - связана с представлениями учащихся о смысле действий сложения и вычитания и с усвоением ими состава одно­ значных чисел. Опираясь на эти знания, учащиеся отвечают на

62

вопрос - сколько единиц осталось во втором слагаемом после то­го, как выполнена первая операция;

в) третья операция - оставшиеся единицы второго слагаемого прибавляются к числу 10.

Таким образом, для овладения данным приемом необходимо прочное усвоение детьми состава каждого числа в пределах 10 и состава двузначного числа из десятков и единиц. Этот прием мож­но представить в виде тождественных преобразований:

8+5 = 8+(2+3) = (8+2)+3 = 10+3=13,

при выполнении которых используется сочетательное свойство сложения или правило прибавления суммы к числу.

Но практика показывает, что большинство семилетних детей с трудом выполняют такую громоздкую запись, поэтому целесооб­разнее использовать другие формы записей. Например:

8 + 5=13 8 + 5=13

2 3 8+2+3 = 13

Число 2 показывает, какое число нужно прибавить к 8, чтобы получить 10. Число 3 - сколько единиц нужно прибавить к 10.

Ш Задание 29. Найдите в учебниках для начальных классов страни­цы, связанные с изучением приема сложения однозначных чисел с пере­ходом через десяток. Проанализируйте приведённые там задания с точки зрения операций, входящих в вычислительный прием. Подумайте, какие формы записи и наглядные пособия можно использовать для усвоения данного приема.

Пользуясь вычислительным приемом, дети постепенно состав­ляют таблицу сложения в пределах 20. Затем все рассмотренные случаи сводятся в общую таблицу, которую учащиеся должны прочно усвоить. В таблице 20 случаев. Она включает сложение одинаковых слагаемых: 6+6, 7+7, 8+8, 9+9 и случаи прибавления меньшего числа к большему. Для прибавления большего числа к меньшему используется переместительное свойство сложения.

Ш Задание 30. После изучения всех случаев сложения однозначных чисел с переходом через десяток учащимся предлагается задание:

63

«Пользуясь таблицей сложения, найди значения выражений: 11-7, 11-5, 12-8, 13-9, 14-7, 15-8».

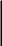
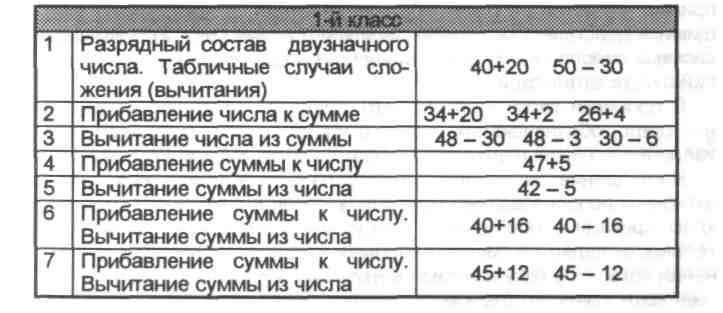
Какой вычислительный прием могут использовать школьники? Опи­шите его. Приведите рассуждения детей.

Для вычитания однозначного числа из двузначного (в пределах 20, с переходом через десяток) обычно используются два вычис­лительных приема. По своей сути они оба знакомы учащимся. В основе одного лежит понятие о взаимосвязи суммы и слагаемых и прочное знание таблицы сложения в пределах 20.

В состав этого приема входят операции:

а) представление уменьшаемого в виде суммы двух слагаемых, одно из которых равно вычитаемому;

б) вычитание из данной суммы слагаемого, равного вычитаемо­ му; в основе этой операции лежит правило: если из суммы вычесть одно слагаемое, то останется другое.

В состав другого приема, который называют отсчитыванием по частям, входят операции:

а) вычитание из данного двузначного числа его разрядных еди­ ниц (в результате выполнения этой операции всегда получается число 10);

б) представление вычитаемого в виде суммы слагаемых, одно из которых равно количеству разрядных единиц двузначного числа (в основе этой операции лежит знание состава однозначных чи­ сел);

в) вычитание из 10 второго слагаемого этой суммы.

II Задание 31. Найдите в учебниках математики для начальных классов упражнения, которые используются при усвоении приемов вычи­тания однозначного числа из двузначного с переходом через десяток, и соотнесите каждое из них с операциями, входящими в состав этих прие­мов. Придумайте сами различные задания, которые можно использовать с этой же целью.