
- •7. Бейтарап берілген күштер жүйесін бір нүктеге шоғырлау.
- •8)Кеңістікте берілген күштер мен жазық күштер жүйесінің аналитикалық тепе-теңдік шарттары. Күштер жүйесінің статикалық анықталынғандық және анықталынбағандық ұғымдары.
- •1 Нүкте қозғалысының векторлық тәсілмен берілуі?
- •3 Нүкте қозғалысының табиғи тәсілмен берілуі
- •4 Нүкте қозғалысының кейбір жеке түрлері
- •5 Қатты дeнeнің ілгерілeмeлі қозғалысы
- •6 Қатты дененің қозғалмайтын өс төңірегіндегі айналмалы қозғалысы
- •7. Қатты дeнeнің жазық параллeль қозғалысының заңы, оның анықталу тәсілдeрі
- •8. Материалық нүктенің кинетикалық моменті. Материалық нүктенің кинетикалық моментінің өзгеруі туралы теорема.
- •10. Механикалық жүйе динамикасы. Жүйе массасы; масса ортасы (центрі). Күштерді топқа бөлу, ішкі күштер ерекшелігі.
- •11. Механикалық жүйе қозғалысының дифференциалдық теңдеулері. Жүйенің масса ортасының қозғалу теоремасы. Масса ортасының қозғалысын сақтау теоремасы.
- •12. Материалдық жүйенің қозғалыс мөлшері. Күштің лездік және толық импульсі. Механикалық жүйе қозғалыс мөлшерінің өзгеру теоремасы. Сақталу теоремасы.
- •14.Күштің элементарлық және толық жұмысы. Қуат.
14.Күштің элементарлық және толық жұмысы. Қуат.
Элементар
жұмыстың векторлардың скалярлық
көбейтіндісі түрінде алынған өрнегінен
сол векторлардың проекциялары арқылы
жазылуына көшуге болады. d’A
= Fxdx
+ Fydy
+ Fzdz
Күштің элементар жұмысын есептеу үшін
тағы бір формула: d’A
=Fdr=Fvdt Элементар жұмыстың әр түрлі
өрнегіне сәйкес,күштің толық жұмысы
да әр түрлі формулалармен сипатталады:
A=
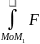 xdx+Fydy+Fzdz,
A=
xdx+Fydy+Fzdz,
A=
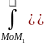 cosα)dS,
A=
vdt
Жұмыс өлшемінің бірлігі үшін 1 Джоуль
алынады.(1ДЖ=1Нм),ал техникалык жуйеде
– 1кГм(1кГм=9,81).
Уақыт бірлігіне қатысты алынған
жұмыс қуат деп аталынады.Қуатты N деп
алсақ,онда оны мына формуламен анықтаймыз:
N=
cosα)dS,
A=
vdt
Жұмыс өлшемінің бірлігі үшін 1 Джоуль
алынады.(1ДЖ=1Нм),ал техникалык жуйеде
– 1кГм(1кГм=9,81).
Уақыт бірлігіне қатысты алынған
жұмыс қуат деп аталынады.Қуатты N деп
алсақ,онда оны мына формуламен анықтаймыз:
N=
 .
Қуат бірлігі үшін
1ватт(1Вт=1Дж/с)алынады.
Жұмысты
есептеу мысалы. Салмағы
2m жүкті горизонтпен 300
бұрыш құратын көлбеу жазықтықтың
бойымен 5м биіктікке көтеру үшін
жұмсалатын ең аз жұмысты анықтау
қажет.Уйкеліс коэффициенті 0.5-ке
тең.Жүкке түсірілген күштер:оның салмақ
күші – P,үйкеліс күші – Fүйк
,
көлбеу жазықтықтың нормаль реакция
күші – N. Шешуі:
жүкке түсірілген күштер жұмыстарының
қосындысы:
∑Аi=A(P)+A(Fүйк)=-mgh-fmghctgα=-mgh(1+fctgα)=-2000*9.81*5(1+0.5*1.732)=
-183000Дж. Модулін қабылдаймыз. А=183кДж
.
Қуат бірлігі үшін
1ватт(1Вт=1Дж/с)алынады.
Жұмысты
есептеу мысалы. Салмағы
2m жүкті горизонтпен 300
бұрыш құратын көлбеу жазықтықтың
бойымен 5м биіктікке көтеру үшін
жұмсалатын ең аз жұмысты анықтау
қажет.Уйкеліс коэффициенті 0.5-ке
тең.Жүкке түсірілген күштер:оның салмақ
күші – P,үйкеліс күші – Fүйк
,
көлбеу жазықтықтың нормаль реакция
күші – N. Шешуі:
жүкке түсірілген күштер жұмыстарының
қосындысы:
∑Аi=A(P)+A(Fүйк)=-mgh-fmghctgα=-mgh(1+fctgα)=-2000*9.81*5(1+0.5*1.732)=
-183000Дж. Модулін қабылдаймыз. А=183кДж
15. Кинетика-қ момент-ң өгеруі туралы теореманы қатты дене-ң айналмалы қозғалысына қолдану. Теорема: Қандай да бір қозғалмайтын центрге қатысты алынған механикалық жүйенің кинетикалық моментінің уақыт бойынша алынған туындысы сол центрге қатысты алынған жүйедегі сыртқы күштердің бас моментіне тең.
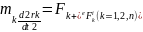 (1)
(1)
Мұндай
теңдеулерді әрбір нүкте үшін құруға
болатындықтан олардың жалпы саны n
жүйедегі нүктелер санына тең болады.
Осы теңдеудегі n теңдеудің әрқайсысына
сәйкес нүктелердің радиус векторы
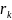 -ге
векторлық түрде көюейтіп, оларды бір-
біріне қосамыз:
-ге
векторлық түрде көюейтіп, оларды бір-
біріне қосамыз:
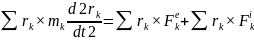 (2)
(2)
Осы теңдеуді ң сол жағын түрлендіреміз:
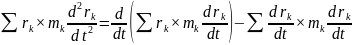 =
=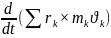 (3)
(3)
Жүйенің ішкі күштерінің қасиеті бойынша ішкі күштердің бас моменті әр уақытта нолге тең болады. Сондықтан да теңдіктің оң жағындағы екінші қосындысы нолге тең:
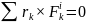 (4)
(4)
(3 ) ті(4 ) ке пайдаланып (2) келтіреміз:
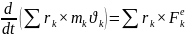
16.
Қатты
дене-ң жылжымайтын ості айналып қозғалу
диф-қ теңдеуі.
Декненің
қозғалмайтын өс төңірегіндегі айналмалы
қозғалысының дифференциалдық теңдеуін
алу үшін кинетикалық моменттің өзгеруі
туралы теореманы
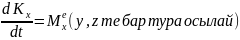
Теңдеулерінің үшінші түріне сәйкес қолдануымыз керек:
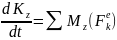
Дененің Z айналу осіне қатысты алынған кинетикалық моменті формулаларының 3-сі бойынша анықталады.
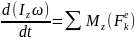
Дене
абсолют қатты дене болған жағдайда
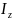 инерция
мометі тұрақты шама болады. Олай болса
алдыңғы теңдеуді былайша өзгерте
аламыз.
инерция
мометі тұрақты шама болады. Олай болса
алдыңғы теңдеуді былайша өзгерте
аламыз.
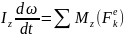 немесе
немесе
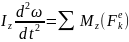
17Мех. жүйе-ң кинет. Эн-ы Ан-ма. Механикалық жүйенің кинетикалық эн-сы деп ондағы барлық материялық нүктелердің кинетикалық эн- ың қосындысына тең скаляр шаманы айтамыз. Массасы m әрбір материялық нүктенің кинетикалық эн-сы:
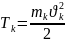 (k=
1,2,n)
(k=
1,2,n)
Онда, анықтама бойынша, n материялық нүктеден тұратын механикалық жүйенің кинетикалық эн-сы осылардын арифметикалық қосындысына тең.
T=
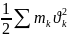 н/е
T=
н/е
T=
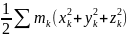
Кинетикалық энергия қозғалыс мөлшерімен қатарлас келетін жүйе қозғалысының негізгі екі өлшемінің бірі болып табылады. Жоғарыда айтқанымыздай, жүйенің қозғалыс мөлшері оның ілгермелі қозғалысын сипаттайды. Ал кинетикалық энергия механикалық қозғалысыты толық көлемінде тереңірек сипаттайды.
Кинет. эн-я ан-ма: нүктенің кинет-қ эн-сы деп- оның массасы мен жылд-ң квад-ң көбейтіндісі-ң жартысыа тең шаманы айтамыз.
Т=
m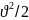
m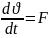 m
m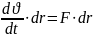
md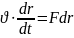 md
md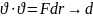 (m
)=Fdr
(m
)=Fdr
 (m
)=
(m
)=
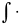 Fdr m
Fdr m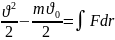
A=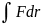 толық
жұмыс
толық
жұмыс
d’A=Fdr элементар жұмыс
Теорема: матер-қ нүкте-ң кинет-қ эн-ң диффер-ы оған әсер ететін күш-ң элементар жұмысына тең.
dT=d’A
Теорема: Нүктенің қандай да бір орын ауыстыру-ғы кинет-қ эн-ң өзгеруі сол орын ауыс-ғы оған әсер етуші күш-ң жұмысына тең.
Динамика? 2 3 4 5
18.Қатты дененің ілгерілмелі, айнымалы ж\е хазық қозғалыстағы кинет. Эн-сы. Ілгерілмелі қозғалыстағы дене нүктелерінің жылдамдықтары өзара тең болғандықтан жылдамдық квадратын ортақ көбейткіш ретінде қосынды белгісінің алдына шығады.
T=1/2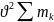
Дене
нүктелерінің массаларының қосындысы
M=
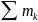 массасые береді. Олай болса ілгерілмелі
қозғалыстағы қатты дене кинетикалық
энергиясы:
массасые береді. Олай болса ілгерілмелі
қозғалыстағы қатты дене кинетикалық
энергиясы:
Т=1/2M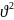
Сонымен, ілгерілмелі қозғалыстағы қатты дененің кинетикалық энергиясы дененің массасы мен оның жылдамдығының квадратының көбейтіндісінің жартысына тең.
Айналмалы қозғалыстағы дене нүктелерінің жылдамдықтары олардың айналу өсіне қашықтықтарына пропорционал болып келеді.
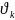 =
=
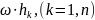
T=1/2 T=1/2
T=1/2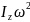
Айналмалы қозғалыстағы қатты дененің кинетикалық энергиясы дененің айналу өсіне қатысты алынған инерция моменті мен оның бұрыштық жылдамдығының квадратына көбейтіндісінің жартысына тең.
