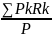8. Материалық нүктенің кинетикалық моменті. Материалық нүктенің кинетикалық моментінің өзгеруі туралы теорема.

Материялық нүктенің қозғалыс мөлшерінің қандайда бір центрге қатысты алынған моментін оның сол центрге қатысты кинетикалық моменті дейді. О центріне қатысты алынған кинет.момент К₀ әрпімен белгілейік. Сонда ол, К₀= r×mv немесе K₀₌ M₀(mv) өрнекпен беріледі. Кинетикалық момент күш әсерінен уақыт өткен сайын өзгеріп отырады. Теңдеудің екі жағын да нүктенің r радиус векторына векторлық түрде көбейтеміз. r×m (1). Бұл теңдеудің сол жағындағы векторлық көбейтіндіні түрлендірейік. r×m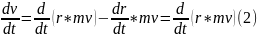 2ші теңдеудің сол жағын 1ші теңдеуге қоямыз. 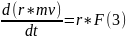. Осы теңдің материялық нүкте қозғалыс мөлшері моментінің өзгеруі туралы немесе басқаша айтқанда, нүктенің кнетикалық моментінің өзгеруі туралы теореманы өрнектейді. Жоғарыда берілген материялық нүктенің кинетикалық моменті деген анықтаманы қолдану арқылы 3ші теңдеуді былай жазамыз. 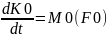(4). 3ші және 4ші тендеумен орнектелетін теорема былай айтылады: қандайда бір центрге қатысты алынған нүкте кинетикалық моментінің уақыт бойынша туындысы сол центрге қатысты күш моментіне тең. Үш өске проекцияласақ:

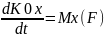
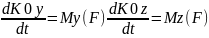(5). 5ші теңдеу кин.момент өзгеруін сипаттайды: координаттар өстеріне қатысты алынған нүкте кинетикалық моменттерінің уақыт бойынша туындылары сол өстерге қатысты алынған күш моменттеріне тең.

9. Материалық нүктенің кинетикалық энергиясы. Материалық нүктенің кинетикалық энергиясының өзгеруі туралы теорема.

Нүктенің кинетикалыө жнергиясы деп оның массасы мен жылдамдығының квадратының көбейтіндісінің жартысына тең болатын скаляр шаманы айтады. Егер нүктенің кинетикалық энергиясын Т деп алсақ, формуласы былай: T= (1). Күш әсерінен нүкте жылдамдығы өзгереді. Сол себепті кинет.энергия да уақыт өткен сайын өзгеріп отырады. 1ші теңдеу екі жағында drға элементар орын ауыстыруға көбейтейік.

m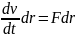 . Бұл теңдеудің сол жағын түрлендірейік: m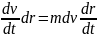 = mdv×v=d(

Нәтижесінде d( =Fdr. Dr элементар орын ауыстыруға күштің элементар жұмысы деп атайды. Элементар жұмысты d’A деп белгілейміз. d’A=Fdr . Кинет.энергия мен элементар жұмыс белгілеулерін пайдаланып dT=d’A. Материялық нүкте өз траекториясын АВ қисығы бойымен М0М1жолын жүреді. Жылдамдығы V₀ ден V₁ ге –өзгереді. М₀M₁ жолындағы күштің толық жұмысы А қисықтың М₀M₁ доғасы бойындағы элементар жұмыстарынан алынған қисық сызықты интегралға тең: A= (2)

Мат.нүктенің бастапқы орындағы кин.энергиясын T₀ деп, ал соңғы орындағысын T₁ белгілесек және күш жұмысын 2ші формуламен өрнектесек: T₁ – T₀ =A. Нүктенің қандай да бір орын ауыстыруындағы кинетикалық энергиясының өзгеруі сол орын ауыстыырудағы оған әсер етуші күштің жұмысына тең.

10. Механикалық жүйе динамикасы. Жүйе массасы; масса ортасы (центрі). Күштерді топқа бөлу, ішкі күштер ерекшелігі.

Механикалық нүктелердің механикалық жүйесі деп қозғалыстары өзара тәуелді болып келетін материялық нүктелер жиынтғын айтады. Егер қозғалыс кезінде жүйедегі нүктелердің бір бірінен ара қашықтықтары өзгермей сақталатын болса, онда бұл жүйені өзгермейтін механикалық жүйе дейміз. Абсолют қатты дене өзгермейтін мех.жүйе ретінде қарастыралады. Берілген мех.жүйе сыртқы күштері деп осы жүйе құрамына енбейтін сыртқы жүйе нүктелерінежасайтын әсерлерінен туатын күштерді айтамыз F деп белгілейміз. Берілген мех.жүйе нүктелерінің арасында болатын өзара әсерлесу күштерін ішкі күштер дейміз. Ішкі күштер берілген жүйе нүктелерінің арасындағы өзара әсер етуші күштер болғандықтан оларға Ньютонның 3-ші заңын қолдана аламыз. Осыдан жүйенің қос қостан алынған ішкі күштер шама жағынан тең,бір түзу бойымен бір біріне қарама қарсы бағытталған күштер жүйесінің бас векторы және кез келген центрге қатысты алынған, олардың бас моменті үнемі нолге тең.

Rⁱ=∑F_k =0 M₀ⁱ=∑M₀(Fk)=0. Бұл күш маңызды қасиет болып табылады.

Мех.жүйе массасы деп ондағы нүктелер массаларының қосындысына тең болатын шаманы айтамыз.

M=∑m_k

Мех.жүйе массаларының центрі деп радиус векторы r=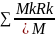

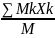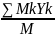Коор.форы: Х_с= Y_с= Z_с=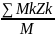

Кейде бұл нүктені мех.жүйенің инерциялар центрі д.ат.

R_k = =
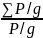