
- •7. Бейтарап берілген күштер жүйесін бір нүктеге шоғырлау.
- •8)Кеңістікте берілген күштер мен жазық күштер жүйесінің аналитикалық тепе-теңдік шарттары. Күштер жүйесінің статикалық анықталынғандық және анықталынбағандық ұғымдары.
- •1 Нүкте қозғалысының векторлық тәсілмен берілуі?
- •3 Нүкте қозғалысының табиғи тәсілмен берілуі
- •4 Нүкте қозғалысының кейбір жеке түрлері
- •5 Қатты дeнeнің ілгерілeмeлі қозғалысы
- •6 Қатты дененің қозғалмайтын өс төңірегіндегі айналмалы қозғалысы
- •7. Қатты дeнeнің жазық параллeль қозғалысының заңы, оның анықталу тәсілдeрі
- •8. Материалық нүктенің кинетикалық моменті. Материалық нүктенің кинетикалық моментінің өзгеруі туралы теорема.
- •10. Механикалық жүйе динамикасы. Жүйе массасы; масса ортасы (центрі). Күштерді топқа бөлу, ішкі күштер ерекшелігі.
- •11. Механикалық жүйе қозғалысының дифференциалдық теңдеулері. Жүйенің масса ортасының қозғалу теоремасы. Масса ортасының қозғалысын сақтау теоремасы.
- •12. Материалдық жүйенің қозғалыс мөлшері. Күштің лездік және толық импульсі. Механикалық жүйе қозғалыс мөлшерінің өзгеру теоремасы. Сақталу теоремасы.
- •14.Күштің элементарлық және толық жұмысы. Қуат.
7. Қатты дeнeнің жазық параллeль қозғалысының заңы, оның анықталу тәсілдeрі
Егер қатты дененің барлық нүктелері қандайда бір қозғал-майтын жазықтыққа параллель қозғалатын болса, онда дененің мұндай қозғалысын жазық – параллель қозғалыс дейміз (2.20-сурет). Қозғалмайтын жазықтық-ты (ж)-деп белгілейік. Дененің О нүктесі арқылы (ж) жазық-тығына параллель етіп (ж) жазықтығы дененің (S) қимасын береді.
Бұл (S) – қиманың барлық нүктелерінің негізгі (ж) – жа-зықтығынан қашықтықтары қоз-ғалыс кезінде өзгермейді, тұрақты болады. Демек, (S) – қимасы үнемі (ж) – жазықтығында жатады және ол өзінің пішінін өзгертпейді.
С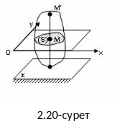 өйтіп,
қатты дененің жазық – параллель
қозғалысын зерттеу оның қозғалмайтын
жазықтыққа параллель қималарының
бірінің мысалы (S)–тің,
жататын (ж)
– жазықтықтың бетімен қозғалуын
зерттеуге келтіріледі. Қозғалмайтын
Ωξηζ
және жазық фигура (S)–ке
қатаң бекітілген Oxyz
координаттар жүйеле-рін таңдап алайық
(2.21-сурет).
өйтіп,
қатты дененің жазық – параллель
қозғалысын зерттеу оның қозғалмайтын
жазықтыққа параллель қималарының
бірінің мысалы (S)–тің,
жататын (ж)
– жазықтықтың бетімен қозғалуын
зерттеуге келтіріледі. Қозғалмайтын
Ωξηζ
және жазық фигура (S)–ке
қатаң бекітілген Oxyz
координаттар жүйеле-рін таңдап алайық
(2.21-сурет).
Қ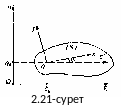 озғалмалы
Oxyz
координаттар жүйесінің бас нүктесі
О-ны
бұдан былай «полюс»-дейміз.
озғалмалы
Oxyz
координаттар жүйесінің бас нүктесі
О-ны
бұдан былай «полюс»-дейміз.
Полюс О-ның өстеріне қатысты координаттарын ξ0 және η0 деп бел-гілейік. Сонда, мына теңдеулер:
![]()
![]()
![]() (2.89)
(2.89)
жазық фигураның қозғалмайтын Ωξη координаттар жазықтығындағы қозғалысын анықтайды. Демек, бұлар жазық фигураның өз жазықтығындағы қозғалысының, күрделі қозғалыс екенін көрсетеді. Оны негізгі екі қүрауышы қозғалысқа жіктеуге болады. Олардың біреуі, жылдамдығы полюс жылдамдығына тең, ілгерілемелі қозғалыс, ал екіншісі, қозғалмайтын центр ретінде қарастырылатын полюс О арқылы өтіп, жазық фигура жазықтығына перпендикуляр орналасатын лездік өс жанындағы, лездік айналыс.
8. Қ.д жазық параллель қозғалысы.Қатты денелердің барлық нүктелері қандай да бір қозғалмайтын жазықтықка параллель қозғалатын болса,онда дененің мұндай қозғалысын жазық параллель қозғалыс дейміз. Жазық фигураның кез келген нүктесінің жылдамдығы полюс жылдымдығымен осы нүктенің полюске қатысты алынған жылдымдығының геометриялық қосындысына тең.
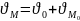
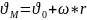
Жазық фигураның кез келген 2 нүктесінің жылдамдықтарының осы нүктелер арқылы жүргізілген түзу бағытындағы проекциялары тең.
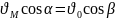
9.Ж:Л.Ц. Ж.л.ц.-берілген лездік уақыт t мезгілінде жылдамдығы 0-ге тең болатын жазық фигура жазықтығының бір нүктесін айтамыз. Егер жазық фигураның қандай да бір нүктесінің жылдамдығы берілсе және 2-шібір нүктенің жылдамдығының бағыты ғана белгілі болса, онда бұл фигура жазықтығының кез келген нүктелерінің жылдамдықтарын жылдамдықтардың лездік центрі арқылы табуға болады.
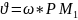
1тәсіл. Жылдамдықтардың таралу формулаларын пайдалану.
2тәсіл. Жылдамдықтар лездік центрін пайдалану.
10.Нүктенің күрделі қозғалысы.
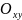 -қозғалмайтын
негізгі санақ жүйесі.
-қозғалмайтын
негізгі санақ жүйесі.
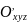 (хуz-
төбесінде штрих)- негізгі жүйеге
қарағанда кез келген түрде қозғалыс
жасай алатын өозғалмалы санақ жүйесі.
(хуz-
төбесінде штрих)- негізгі жүйеге
қарағанда кез келген түрде қозғалыс
жасай алатын өозғалмалы санақ жүйесі.
М
материалық нүкте қозғалатын санақ
жүйеге қарағанда өзі де қозғалыс жасайды
және оның бұл қозғалысы
(хуz-
төбесінде штрих) жүйе қозғалысына
тәуелсіз болады. Негізгі
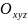 жүйеге қатысты нүктенің қозғалысын
шартты түрде абсолют
немесе күрделі қозғалыс
деп атайды.
жүйеге қатысты нүктенің қозғалысын
шартты түрде абсолют
немесе күрделі қозғалыс
деп атайды.
М материалық нүктенің қозғалмалы (хуz- төбесінде штрих) жүйесіне қатысты қозғалысы салыстырмалы қозғалыс ретінде алынады.
Қозғалушы М материалық нүктенің жылжымалы жүйе (хуz- төбесінде штрих) жүйесіне ілесе қозғалуы оның тасымал қозғалыс ретінеде алынады.
11. Жылдамдықтарды қосу теоремасы.
Нүктенің абсолют жылдамдығы тасымал және салыстырмалы жылдамдықтардың векторлық қосындысына тең болады.
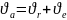
Нүктенің абсолют үдеуі тасымал,салыстырмалы және Кориолис үдеулерінің геометриялық қосындысына тең болады.
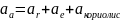
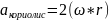
Динамика
1.Динамика мәселелері. Динамикада материалық нүкте мен материалық дененің қозғалыстары оларды болдыратын физикалық себептермен, яғни күштермен тығыз байланысты қарастырады. Денеге түсірілген күштер мен олардың әсерінен болатын қозғалыс арасындағы тәуелділікті зерттеу. Сөйтіп қозғалыстың жалпы заңдылығын табу мәлелелері қарастырылады.
Материялық нүкте деп қозғалыстың берілген жаңдайларында өлшемдерін ескермеуге болатын денені айтамыз.
Дененің материя мөлшерінің өлшемі ретінде алынатын, P/g=const=m- қатынаспен анықталатын, шаманы дененің ауырлық (гравитациялық) массасы дейді.
Материялық денелердің механикалық өзара әсерлесуінің өлшемі ретінде алынатын шаманы механикада күш деп атайды. Күш-векторлық шама. 1-шамасына, 2-бағытына, 3-түсу нүктесіне тәуелді.Халықаралық жүйеде 1Н, ал бірліктердің техникалық жүйесінде 1кГ.
6. Кедергі жылдамдыққа үлесті (пропорционал) болғандағы кедергісіз ортада нүктенің еріксіз (мәжбүрлі) тербелісі. Резонанс жағдайы.
R=0 b=0
X=asin(nt+E)+P\(n2-p2)sin[(pt+∂)-α]
A=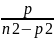 A мәжбүрлі тербелістер амплитудасы
A мәжбүрлі тербелістер амплитудасы
Егер мәжбүр етуші Q күшінің жиілігі және өзіндік тербелістердің жиілігі өзара теңесіп кетсе, яғни p=n онда А>∞ болады, осы кезде резонанс деп аталатын құбылыс пайда болады.
7. Материалық нүктенің қозғалыс мөлшері. Күштің элементар және толық импульсі. Қозғалыс мөлшерінің өзгеруі туралы теорема.
Материялық нүктенің м массасы мен V жылдамдығының көбейтіндісіне тең q=mv векторын оның қозғалыс мөлшері дейміз. Q векторы нүктеге түсірілген Ғ күші әсерінен уақыт өткен сайын өзгеріп отырады.
m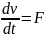 немесе
немесе
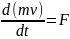 .
Теңдеудің екі жағында dt-ға көбейтеміз.
.
Теңдеудің екі жағында dt-ға көбейтеміз.
D(mv)=Fdt. Fdt көбейтіндісін күштің элементар импульсі деп атайды. Теорема түрінде былай: материялық нүктенің қозғалыс мөлшерінің дифференциалы күшінің импульсына тең. Уақыт t=t0 болған нүкте жылдамдығы v=v0 болады дейік. Теңдіктің сол жағын Vдан V0 дейінгі шектерде, ал оң жағынан t0 ден t ға дейінгі шектерді интегралды алайық:
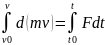 mv-mv0=
mv-mv0=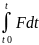 (1)
(1)
Элементар импульстерден t=t0 уақыт аралығында алынған интегралмен анықталатын S векторын күштің сол уақыт аралығындағы импульсі деп атайды.
S= Күш импульсінің координаттар өстеріндегі проекциялары мынадай теңдіктермен анықталады.
S x=
x=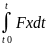 Sy=
Sy=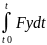 Sz=
Sz=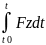 mv-mv0
=
S (2)
mv-mv0
=
S (2)
1 және 2 теңдіктері материялық нүктенің қозғалыс мөлшерінің өзгеруі туралы теорема: қандай да уақыт аралығындағы нүктенің қозғалыс мөлшерлерінің өзгеруі сол уақыт аралығындағы күш импульсіне тең.
Теореманың координаттық өстерге проекциясы былай айтылады: нүктенің өозғалыс мөлшерінің берілген өстегі проекциясының қандайда бір уақыт аралығындағы өзгеруә сол уақыт аралығындағы күш импульсінің осы өстегі проекциясына тең.
