
- •Московский технический университет связи и информатики
- •1. Цель работы.
- •2. Исходные данные для выполняемого варианта (вариант №7, усложненный).
- •3. Результаты выполнения курсовой работы.
- •3.1. Таблица истинности устройства.
- •3.2. Скнф логических функций.
- •3.3. Сднф логических функций.
- •3.4. Мкнф логических функций.
- •3.5. Мднф логических функций.
- •3.6. Представление логических функций в базисе или-не.
- •3.7. Представление логических функций в базисе и-не.
- •3.8. Разработка модулей, реализующих отдельные логические функции и устройство в целом.
- •3.9. Rtl схемы синтезированных устройств.
- •3.10. Моделирование разработанных модулей в симуляторе iSim.
- •3.11. Формирование конфигурационного файла и оценка требуемых ресурсов плис.
3.5. Мднф логических функций.
Минимизацию логических функций проведем с помощью карт Карно.
При нахождении МДНФ данный метод отличается от того, как находили МКНФ, следующим. Сначала вместо лог. 0 выделяются лог. 1. Дизъюнкция заменяется конъюнкцией, и наоборот. Инвертируются те аргументы, значение которых равно лог. 0.
Y1:
X3X4
X1X2 |
00 |
01 |
11 |
10 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
11 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
Область |
Набор значений аргументов |
1 (с) |
0010 |
2 (к) |
010* |
3 (з) |
*101 |
4 (ф) |
1000 |
МДНФ для функции Y1 имеет следующий вид:

Y2:
X1X2 |
00 |
01 |
11 |
10 |
0 |
0 |
1 |
1 |
0 |
01 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
10 |
0 |
1 |
1 |
0 |
Область |
Набор значений аргументов |
1 (к) |
*0*1 |
2 (ф) |
0*01 |
3 (з) |
1*11 |
МДНФ для функции Y2 имеет следующий вид:

Y3:
X3X4
X1X2 |
00 |
01 |
11 |
10 |
00 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
11 |
0 |
0 |
0 |
0 |
10 |
0 |
0 |
0 |
0 |
Область |
Набор значений аргументов |
1 |
0111 |
МДНФ для функции Y3 имеет следующий вид:
3.6. Представление логических функций в базисе или-не.
Представление логической функции в базисе ИЛИ-НЕ проведем с помощью МКНФ.
Сначала функция дважды инвертируется, а затем преобразуется с помощью формул де Моргана.



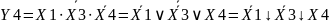

3.7. Представление логических функций в базисе и-не.
Представление логической функции в базисе И-НЕ проведем с помощью МДНФ.
Сначала функция дважды инвертируется, а затем преобразуется с помощью формул де Моргана.


Для
представления в базисе И-НЕ логических
функций Y3
и Y4,
кроме инверсии и формул де Моргана,
воспользуемся правилом:
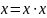 .
.




 0
0
 1
1 0
0 X3X4
X3X4 0
0
 1
1 1
1