6. Метод анализа для проверки гипотезы
ЧСС
1 гр. |
71 |
82 |
75 |
86 |
60 |
74 |
60 |
84 |
67 |
80 |
79 |
68 |
78 |
65 |
75 |
2 гр. |
68 |
56 |
70 |
70 |
65 |
82 |
71 |
65 |
74 |
59 |
80 |
63 |
64 |
70 |
50 |
1.Н(0)- значение ЧСС у взрослых и детей одинаково.
H(1)- значение ЧСС у взрослых и детей различно.
2. Задаём уровень значимости: α=0.01
3. Закон распределения не известен, данные количественные, выборки не зависимые.
4.
Непараметрический U-критерий
Манна-Уитни для независимых выборок: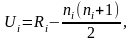
где i
= 1 и 2 – номер выборки
5.Ранжируем обе выборки и присваиваем ранги.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
50 |
56 |
59 |
60 |
60 |
63 |
64 |
65 |
65 |
65 |
67 |
68 |
68 |
70 |
70 |
70 |
71 |
71 |
74 |
74 |
75 |
75 |
78 |
79 |
80 |
80 |
82 |
82 |
84 |
86 |
1 |
2 |
3 |
4,5 |
4,5 |
6 |
7 |
9 |
9 |
9 |
11 |
12,5 |
12,5 |
15 |
15 |
15 |
17,5 |
17,5 |
19,5 |
19,5 |
21,5 |
21,5 |
23 |
24 |
25,5 |
25,5 |
27,5 |
27,5 |
29 |
30 |
R1(взрослых)=265,5
R2(детей)=184,5
Uвыч (взрослых)=265,5-(15*(15+1))/2= 145,5
Uвыч (детей)= 184,5-(15*(15+1))/2=64,5
За вычисленный критерий берём наименьшее: Uвыч=64,5
Uкрит=51
α=0,01 n1=15 n2=15
Н(0 ) принимается т.к. Uвыч. ˃Uкрит.
Вывод: значение ЧСС у взрослых и детей одинаково.
ВЕС
1 гр. |
85 |
60 |
68 |
59 |
64 |
65 |
70 |
89 |
60 |
87 |
62 |
76 |
75 |
98 |
65 |
2 гр. |
52 |
40 |
34 |
46 |
43 |
40 |
52 |
50 |
38 |
38 |
45 |
55 |
48 |
52 |
35 |
1. Н(о)- вес у взрослых и детей одинаковый.
Н(1)- вес у взрослых и детей различный.
2. Задаём уровень значимости: α=0.01
3. Закон распределения не известен, данные количественные, выборки не зависимые.
4. Непараметрический U-критерий Манна-Уитни для независимых выборок: где i = 1 и 2 – номер выборки
5.Ранжируем обе выборки и присваиваем ранги.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19
|
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
35 |
35 |
39 |
40 |
40 |
40 |
40 |
42 |
45 |
50 |
50 |
50 |
52 |
52 |
55 |
59 |
60 |
60 |
62 |
64 |
65 |
65 |
68 |
70 |
75 |
76 |
85 |
88 |
89 |
99 |
1,5 |
1,5 |
3 |
5,5 |
5,5 |
5,5 |
5,5 |
8 |
9 |
11 |
11 |
11 |
13,5 |
13,5 |
15 |
16 |
17,5 |
17,5 |
19 |
20 |
21,5 |
21,5 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
R1 (Взрослых) =345
R2 (Детей) =118
Uвыч(взрослых)= 345 - (15*(15+1))/2=225
Uвыч(детей)= 118 - (15*(15+1))/2=-2
За вычисленный критерий берём наименьшее: Uвыч= -2
Uкрит =51
α=0,01 n1=15 n2=15
Н(0) отвергается, и принимается Н(1) т.к. Uвыч. < Uкрит.
Вывод: вес у взрослых и детей различный, с уровнем значимости α=0,01.