1. Коды Малера.
Коды
Рида-Маллера относятся к линейным
двоичным кодам, имеющим большие кодовые
расстояния и исправляющим благодаря
этому много ошибок. Они пригодны для
каналов с малым отношением сигнал/помеха.
Этот класс кодов интересен и потому,
что с ним связаны многие другие сигналы,
применяемые в радиотехнических системах:
ортогональные и биортогональные сигналы,
симплексные коды, 
-последовательности
и коды Хэмминга.
Кодовое
слово длины 
обычно
рассматривается как булева функция
(или ее инверсия), заданная в 
точках,
т.е. на наборах из 
двоичных
элементов. Можно многими способами
нумеровать позиции кодового
слова
-разрядными
двоичными векторами. Ясно, что, как в
случае кодов Хэмминга, такая перестановка
не влияет на помехоустойчивость
получаемых кодов. Будем нумеровать
позиции кодового слова числами в двоичной
системе счисления 
,
где 
для 
.
Ввиду линейности кодов Рида-Маллера
каждый символ кодового слова 
представим
линейной комбинацией
|
|
,или ее инверсией
|
|
,где 
–
известные информационные символы.
В
соответствии с определением порождающей
матрицы (5.16) и правилом покомпонентного
сложения векторов элементы 
являются
столбцами матрицы 
.
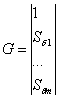
Для 
порождающая
матрица размера 
на 
имеет
вид:
|
|
.Столбцы матрицы без верхней строки представляют собой последовательность чисел, записанных в двоичной системе счисления (младшие разряды внизу). Таким образом, столбцы матрицы можно рассматривать как последовательность состояний двоичного суммирующего счетчика:
|
(5.34) |
,где
1 – последовательность из единиц; 
–
последовательность состояний последнего
(старшего) разряда счетчика; 
–
последовательность состояний первого
(младшего) разряда. Отметим, что
перестановка столбцов и строк порождающей
матрицы приводит к эквивалентным кодам.
2. Сжатие данных.
Сжатие данных (англ. data compression) — алгоритмическое преобразование данных, производимое с целью уменьшения занимаемого ими объёма. Применяется для более рационального использования устройств хранения и передачи данных. Синонимы — упаковка данных, компрессия, сжимающее кодирование, кодирование источника. Обратная процедура называется восстановлением данных (распаковкой, декомпрессией).
Сжатие основано на устранении избыточности, содержащейся в исходных данных. Простейшим примером избыточности является повторение в текстефрагментов (например, слов естественного или машинного языка). Подобная избыточность ссылкой на уже закодированный фрагмент с указанием его длины. Другой вид избыточности связан с тем, что некоторые значения в сжимаемых данных встречаются чаще других. Сокращение объёма данных достигается за счёт замены часто встречающихся данных короткими кодовыми словами, а редких — длинными (энтропийное кодирование). Сжатие данных, не обладающих свойством избыточности (например, случайный сигнал илибелый шум, зашифрованные сообщения), принципиально невозможно без потерь.обычно устраняется заменой повторяющейся последовательности