3. Как называется канал связи, в котором действует аддитивная помеха типа «белого шума» с нормальным законом распределения мгновенных значений?

1. Регистры сдвига.

Регистры – это последовательностное логическое устройство, используемое для хранения n-разрядных двоичных чисел и выполнения преобразований над ними. Регистр представляет собой упорядоченную последовательность триггеров, число которых соответствует числу разрядов в слове.

Регистры сдвига предназначены для преобразования информации путем ее сдвига под воздействием тактовых импульсов. Такие регистры представляют совокупность последовательно соединенных триггеров, как правило, двухступенчатой структуры. Число триггеров определяется разрядностью записываемого слова. По направлению сдвига информации различают регистры прямого сдвига (вправо, т. е. в сторону младшего разряда), обратного сдвига (влево,  т. е. в сторону старшего разряда) и реверсивные, допускающие сдвиг в обоих направлениях.

Наиболее широко распространены регистры сдвига на D-триггерах со статическим (рис. 2.39) или с динамическим управлением. Такие регистры имеют один информационный вход, вход для тактовых импульсов (импульсов сдвига) и установочный вход. Выходы в регистре могут быть с каждого разряда для считывания информации одновременно со всех разрядов, т. е. параллельным кодом.

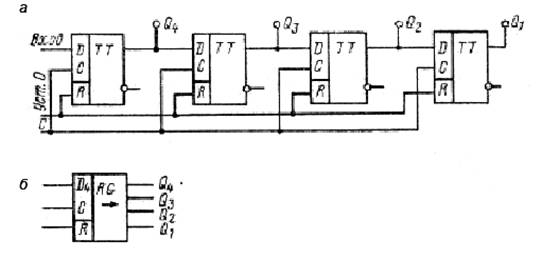
Рис. 2.39. Регистр сдвига: а – функциональная схема; б – условное обозначение

 

Также может быть один выход с последнего относительно  входа разряда для считывания информации последовательно во времени, т. е. последовательным кодом.

Вход регистра для импульсов сдвига получается объединением  С-входов вcex триггеров, а установочный вход – R-входов.

2. Шифраторы и дешифраторы.

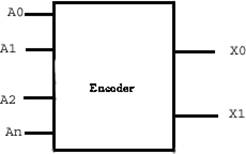
Шифратор (кодер) — (англ. encoder) логическое устройство, выполняющее преобразование позиционного кода в n-разрядный двоичный код. Шифратор выполняет функцию преобразования унарного кода в двоичный. При подаче сигнала на один из входов (обязательно на один, не более) на выходе появляется двоичный код номера активного входа.   

Если количество входов настолько велико, что в шифраторе используются все возможные комбинации сигналов на выходе, то такой шифратор называется полным, если не все, то неполным. Число входов и выходов в полном шифраторе связано соотношением:   где n — число входов,m — число выходов. Приоритетный шифратор отличается от шифратора наличием дополнительной логической схемы выделения активного уровня старшего входа для обеспечения условия работоспособности шифратора (только один уровень на входе активный). Уровни сигналов на остальных входах схемой игнорируются. Дешифратор - это логическое устройство, работающее следующим образом: он получает на вход закодированный сигнал (двоичный, двоично-десятичный и т.п.), и выдает его на одном из n своих выходов. Существуют другие дешифраторы, преобразующие один код в другой.  Число входов дешифратора обычно меньше числа выходов.

3. Циклические коды, их свойства и математическое представление.

Циклические коды являются частным случаем линейных и представляют собой наиболее разработанную часть последних. Основным их достоинством является простота технической реализации, благодаря чему они и обратили на себя внимание специалистов. Ценным свойством таких кодов является способность обнаруживать не только одиночные ошибки, но и пакеты ошибок. Пакетом ощибок длиной L называют число разрядов сообщения, искаженных подряд.  Свое название циклические коды получили из-за следующего свойства: если комбинация  a_n-1a_n-2 ... a₁a₀

относится к коду, то комбинация, полученная путем циклического сдвига элементов, т.е. комбинация  a_n-2 ... a₁a₀a_n-1,

также относится к коду. Направление сдвига не имеет значения. Один сдвиг в одном направлении эквивалентен n-1 сдвигам в другом направлении.

Математической основой построения циклических кодов является представление кодовых комбинаций в виде многочленов от некоторой переменной x с коэффициентами, равными элементам кодовых комбинаций, и операцией по mod2. Кодовая комбинация 

a_n-1a_n-2 ... a₁a₀

представляется многочленом  a_n-1x^n-1 + a _n-2x^n-2 + ... + a₁x + a₀

Циклический код строится с помощью так называемого порождающего многочлена g(x) степени r. Признаком принадлежности n-разрядной комбинации данному коду является делимось соответствующего ей многочлена на порождающий. Если многочлен принятой комбинации делится на порождающий, то считается, что она совпадает с посланной. Если деление происходит с остатком, то принятая комбинация к коду не относится, т.е. произошло наложение ошибки. Вид остатка при достаточной избыточности позволяет указать место ошибки.