
- •1 Аналоговые и дискретные сигналы.
- •2 Модель канала связи с аддитивным шумом.
- •1 Беспроводные радиоканалы.
- •2. Помехи в каналах.
- •3. Какие функции выполняют кодеры и декодеры?
- •1. Коды Малера.
- •2. Сжатие данных.
- •1. Коды Рой-Чаудхури, Гоппа.
- •2. Алгоритмы цифрового кодирования.
- •1. Код Хаффмана.
- •2. Демодуляция и обнаружение цифровых сигналов.
- •1. Кодеры и декодеры.
- •2. Проводные и волоконно-оптические каналы связи.
- •1. Коды Малера, Рида, Соломона, Рой-Чаудхури, Гоппа.
- •2. Импульсно-кодовая модуляция.
- •3. Основные параметры сигналов: длительность, ширина спектра и динамический диапазон. Примеры: речевые (телефонные), вещательные, телевизионные, телеграфные сигналы, сигналы передачи данных.
- •1. Каналы связи и их характеристики.
- •2. Цифровые системы передачи.
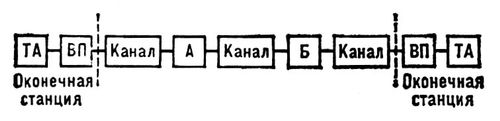
- •3. Схема организации цифровой телефонной связи.
- •1. Кодеры и декодеры.
- •2. Проводные и волоконно-оптические каналы связи.
- •1. Линейные двоичные коды для обнаружения и исправления ошибок.
- •2. Ацп последовательного счета.
- •1. Методы декодирования корректирующих кодов.
- •2. Теорема Котельникова.
- •1. Многопозиционная модуляция.
- •2. Коды Хемминга.
- •1. Модель Гильберта.
- •2. Алгоритм декодирования Витерби.
- •3. Основные параметры сигналов.
- •1. Методы уплотнения.
- •2. Методы повышения верности передачи информации.
- •3. Частотная модуляция, способы получения чм колебаний.
- •Псевдотроичный метод кодирования.
- •2. Схема параллельного аналого-цифрового преобразователя.
- •1. Проводные и волоконно-оптические каналы связи.
- •2. Коды с гарантированным обнаружением и исправлением ошибок.
- •1. Принцип преобразования неподвижного изображения в электрический сигнал.
- •2. Регистры памяти.
- •3. Цифровые виды модуляции.
- •1. Преобразование звукового сигнала в цифровой сигнал.
- •2. Схема организации телеграфной связи.
- •Фазовая модуляция в цифровой системе связи.
- •1. Работы Хартли и Винера.
- •2. Мажоритарное декодирование.
- •3. Как называется канал связи, в котором действует аддитивная помеха типа «белого шума» с нормальным законом распределения мгновенных значений?
- •Регистры сдвига.
- •2. Шифраторы и дешифраторы.
- •3. Циклические коды, их свойства и математическое представление.
- •1. Схема цифровой системы связи.
- •2. Коды Соломона.
- •3. Если сигнал и шум независимые случайные процессы, то в каком канале связи дисперсии сигнала и шума складываются.
- •1. Телеграф Морзе.
- •2. Корреляционный приемник. Методы декодирования корректирующих кодов.
- •3. Какая из помех перемножается с сигналом.
- •Теория Найквиста.
- •2. Цифровые модуляции.
- •1. Цифровой согласованный фильтр.
- •2. Теорема Шеннона.
- •1. Циклические коды.
- •2. Методы цифровой полосовой модуляции.
- •1. Узкополосная передача.
- •2. Блочные корректирующие коды.
- •3. Что такое дисперсия случайного процесса?
2. Схема организации телеграфной связи.
Фазовая модуляция в цифровой системе связи.
Фа́зовая
модуля́ция —
один из видов модуляции колебаний,
при которой фаза несущего
колебания управляется информационным
сигналом. Фазомодулированный сигнал ![]() имеет
следующий вид:
имеет
следующий вид:
![]() ,
,
где ![]() —
огибающая сигнала;
—
огибающая сигнала; ![]() является
модулирующим сигналом;
является
модулирующим сигналом; ![]() —
частота несущего сигнала;
t — время.
—
частота несущего сигнала;
t — время.
Фазовая модуляция, не связанная с начальной фазой несущего сигнала, называется относительной фазовой модуляцией (ОФМ).
1. Работы Хартли и Винера.
Теорема
Шеннона — Хартли в теории
информации —
применение теоремы кодирования канала
с шумом к архетипичному случаю непрерывного
временно́го аналогового канала
коммуникаций, искажённого гауссовским
шумом.
Теорема устанавливает шенноновскую
ёмкость канала, верхнюю границу
максимального количества безошибочных
цифровых данных (то есть, информации),
которое может быть передано по такой
связи коммуникации с указанной полосой
пропускания в присутствии шумового
вмешательства, согласно предположению,
что мощность сигнала ограничена, и
гауссовский шум характеризуется
известной мощностью или мощностью
спектральной плотности. Закон назван
в честь Клода
Шеннона и Ральфа
Хартли.
Рассматривая все возможные многоуровневые
и многофазные методы шифрования, теорема
Шеннона — Хартли утверждает, что
пропускная способность канала ![]() ,
означающая теоретическую верхнюю
границу скорости передачи данных,
которые можно передать с данной средней
мощностью сигнала
,
означающая теоретическую верхнюю
границу скорости передачи данных,
которые можно передать с данной средней
мощностью сигнала ![]() через
аналоговый канал связи, подверженный
аддитивному белому гауссовскому шуму
мощности
через
аналоговый канал связи, подверженный
аддитивному белому гауссовскому шуму
мощности ![]() равна:
равна:
![]()
где
— пропускная способность канала, бит/с;
![]() —
полоса
пропускания канала, Гц;
—
полоса
пропускания канала, Гц;
— полная мощность сигнала над полосой пропускания, Вт или В²;
— полная шумовая мощность над полосой пропускания, Вт или В²;
— частное от деления отношения сигнала к его шуму (SNR) на гауссовский шум, выраженное как отношение мощностей.
2. Мажоритарное декодирование.
Мажоритарное декодирование тоже базируется на системе проверочных равенств. Система последовательно может быть разрешена относительно каждой из независимых переменных, причем в силу избыточности это можно сделать не единственным способом.
Любой символ ai, выражается d (минимальное кодовое расстояние) различными независимыми способами в виде линейных комбинаций других символов. При этом может использоваться тривиальная проверка ai = ai. Результаты вычислений подаются на соответствующий этому символу мажоритарный элемент. Последний представляет собой схему, имеющую d входов и один выход, на котором появляется единица, когда возбуждается больше половины его входов, и нуль, когда возбуждается число таких входов меньше половины. Если ошибки отсутствуют, то проверочные равенства не нарушаются, и на выходе мажоритарного элемента получаем истинное значение символа. Если число проверок d (2s + 1) и появление ошибки кратности s и менее не приводит к нарушению более s проверок, то правильное решение может быть принято по большинству неискаженных проверок. http://peredacha-informacii.ru/ Чтобы указанное условие выполнялось, любой другой символ aj ( j неравно i) не должен входить более чем в одно проверочное равенство. В этом случае мы имеем дело с системой разделенных проверок.
