2. Теорема Котельникова.

Теоре́ма Коте́льникова (в англоязычной литературе — теорема Найквиста — Шеннона или теорема отсчётов) гласит, что, если аналоговый сигнал   имеет конечный (ограниченный по ширине) спектр, то он может быть восстановлен однозначно и без потерь по своим отсчётам, взятым с частотой, большей или равной удвоенной верхней частоте  :

Такая трактовка рассматривает идеальный случай, когда сигнал начался бесконечно давно и никогда не закончится, а также не имеет во временно́й характеристике точек разрыва. Именно это подразумевает понятие «спектр, ограниченный частотой  ».

Разумеется, реальные сигналы (например, звук на цифровом носителе) не обладают такими свойствами, так как они конечны по времени и обычно имеют разрывы во временно́й характеристике. Соответственно, их спектр бесконечен. В таком случае полное восстановление сигнала невозможно и из теоремы Котельникова вытекают два следствия:

Любой аналоговый сигнал может быть восстановлен с какой угодно точностью по своим дискретным отсчётам, взятым с частотой  , где   — максимальная частота, которой ограничен спектр реального сигнала;

Если максимальная частота в сигнале превышает половину частоты дискретизации, то способа восстановить сигнал из дискретного в аналоговый без искажений не существует.

Говоря шире, теорема Котельникова утверждает, что непрерывный сигнал   можно представить в виде интерполяционного ряда:

где   — функция sinc. Интервал дискретизации удовлетворяет ограничениям   Мгновенные значения данного ряда есть дискретные отсчёты сигнала  .

1. Многопозиционная модуляция.

Анализ методов модуляции, рассмотренных в п.3.2, показывает, что двоичные системы передачи имеют максимальную удельную скорость передачи 2 бит/с*Гц, которую иногда называют скоростью Найквиста.

Повысить удельную скорость передачи информации можно за счет использования m -позиционной АМ или ОФМ. В этом случае один элемент линейного сигнала несет информацию о большем числе символов данных, чем в двоичных (двухпозиционных) системах.

Рассмотрим идею формирования m -позиционных методов модуляции на примере двукратной и трехкратной ОФМ с помощью амплитудно-фазовых (векторных) диаграмм.

На рис.3.16 представлены амплитудно-фазовые диаграммы дня ОФМ, ДОФМ, ТОФМ.

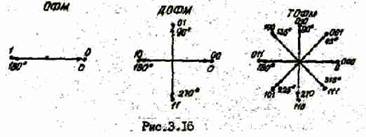
Как видно из рис.3.16, для ОФМ число значащих позиций сигнала данных m=2 со значениями фазы  0°, что соответствует символу 0, и  1800 -символу 1. При ДОФМ m=4 со значениями фаз 00, 900, 1800, 2700 и каждому вектору сигнала ставиться в соответствие два бита данных (дибита) 00, 01, 10, 11. аналогично при ТОФМ m=8 со значениями фаз 00, 450, 900, … 3150 и каждый векторсигнала соответствует трем битам данных (трибитам) 000, 001, … 111.

Число двоичных символов данных k, равное кратности фаз, из-за удобства реализации должно быть целым. Для ОФМ k=1, для ДОФМ k=2 и для ТОФМ k=3. С числом значащих позиций сигнала данных m оно связано соотношением  .

2. Коды Хемминга.

Код Хэмминга, являющийся групповым (n,k) кодом, с минимальным расстоянием d=3  позволяет обнаруживать и исправлять однократные ошибки. Для построения кода Хэмминга используется матрица H.      ,   где A_k- транспонированная подматрица, E_n-k - единичная подматрица порядка n-k.

Если Х - исходная последовательность, то произведение Х·Н=0. Пусть E- вектор ошибок. Тогда  (Х+Е)·Н = Х·Н+Е·Н = 0+Е·Н=E·H - синдром или корректор, который позволяет обнаружить и исправить ошибки. Контрольные символы    e₁ ,e₂ ,...,e_r  образуются из информационных символов, путем линейной комбинации     ,  где  а_j={0,1} - коэффициенты, взятые из подматрицы A матрицы H.     

Рассмотрим Построение кода Хэмминга для k=4 символам. Число контрольных символов r=n-k можно определить по неравенству Хэмминга    для однократной ошибки. Но так, как нам известно, только исходное число символов k, то проще вычислить по эмпирической формуле  

                                       ,                                 (5.2)

где [.] - означает округление до большего ближайшего целого значения. Вычислим для k=4     . Получим код (n,k)=(7,4);      n=7; k=4; r=n-k=3; d=3. Построим матрицу H.

Контрольные символы e_j  определим по формуле   .

3. Общие сведения о цифровой передаче непрерывных сообщений. Постановка задачи об оптимальном демодуляторе (приемнике) дискретных сообщений. Оптимальный прием в дискретно-непрерывном канале без искажений при наличии аддитивного белого шума.

Для передачи непрерывных сигналов можно использовать дискретный канал, преобразуя непрерывный сигнал в цифровой с помощью АЦП, а на приемной стороне цифровой сигнал в непрерывный с помощью ЦАП.

Применение цифровых систем передачи (ЦСП) дает возможность объединения различных видов связи на единой цифровой основе, а также широко использовать современную элементную базу, обеспечивая стабильность характеристик, надежность, и хорошие массо-габаритные показатели.

Принцип АЦП на основе импульсно-кодовой модуляции (ИКМ) включает дискретизация во времени, квантование по уровню (амплитуде) и кодирование [5, 6, 18, 20, 21].

Процесс формирования ИКМ сигнала поясним с помощью упрощенной структурной схемы (рис.6.8) и временных диаграмм (рис. 6.9).

Дискретизация заключается в том, что непрерывный сигнал   (рис. 6.9,а) заменяется отсчетами   (на рис. 6.9,б), следующими через одинаковые интервалы времени  . Например, для речевого сигнала, где  , принят стандартный интервал  ,  .

Процесс дискретизации эквивалентен импульсной модуляции. Для примера на рис. 6.9,б приведен случай АИМ.

Различают равномерное и неравномерное квантование. При квантовании устанавливается количество уровней   разрешенных для передачи.

Процесс квантования состоит в следующем текущие значения сигнала соответствующее моменту отсчета   заменяется ближайшим дискретным значением   (уровнем), такая операция подобна округлению и приводит к ошибке:

,