Изучение нового материала

Начнем с примеров из жизни.

1. Вам необходимо доставить тяжелую коробку на 20 этаж высотного здания. У вас есть выбор: идти по лестнице и ехать в лифте. Какой вариант вы выберите и почему?

- В обоих случаях совершается механическая работа и при этом она будет одинаковой. Конечно же, большинство из вас выберут, лифт. Разница при выполнении одной и той же работы – разное время.

2. По горизонтальной плоскости двигается трактор. Со стороны трактора действует на прицеп постоянная сила тяги. Под действием этой силы прицеп можно перемещать на 2 км и на 4 км. В чем отличие этих перемещений.

Между этими перемещениями имеется отличие и для характеристики этого отличия понятия силы недостаточно. Для этого вводится еще одно понятие – работа. В обыденной жизни под словом «работа» мы называем различные действия человека или устройства. Например, мы говорим: работает врач, продавец, пылесос, компьютер. В физике также существует понятие «работа», но его смысл несколько отличается от привычного. Физика прежде всего, изучает физическую величину, которая называется «механической работой».

Механическая работа совершается , если выполняются следующие условия:

1.На тело действует сила.

2.Тело перемещается под действием этой силы.

Нетрудно понять. Что чем большая сила действует на тело и чем длиннее путь, который проходит тело под действием этой силы, тем большая совершается работа.

Вывод: механическая работа прямо пропорциональна силе и прямо пропорциональна пройденному пути.

Работа является пространственной характеристикой действия силы. Введена по аналогии с ее временной характеристикой – импульсом силы, так как воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений тел.

Работа – физическая величина, равная произведению проекции силы на ось на перемещение по этой оси.

Исторически термин работа ввел французский ученый Ж. Понселе. Для него работа, как понятие, была связана с деятельностью человека.

Сила и перемещение – величины векторные. Но работа равна произведению модулей этих векторов, а модуль вектора – величина скалярная. О работе нельзя сказать, что она куда-то направлена. В выражении на движущееся тело может действовать не одна, а несколько сил. В этом случае в выражении для работы стоит модуль равнодействующей всех сил.

• Пусть тело под действием постоянной силы F переместилось на расстояние S. Тогда возможны варианты в расчете механической энергии.

1. Если направление движения тела S совпадает с направлением действия силы F, то сила совершает положительную работу: A = F∙S

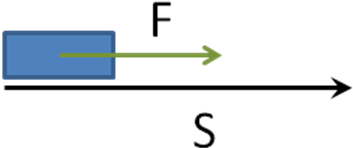
2. Если направление движения тела S противоположно направлению действия силы F, то сила совершает отрицательную работу: A = - F∙S

3. Если под действием силы тело не перемещается, т.е. S =0, работа силы также равна нулю: A = 0

Силы, действующие на тело, могут образовывать с направлением перемещения угол, отличный от 0˚ и 180˚. Например к санкам, движущимся по горизонтальной дороге, в какой-то момент подействовала сила, направленная под углом α к горизонту. Проецирование силы на ось соответствующую перемещению приводит к следующему результату:

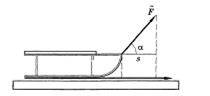
, - угол между векторами силы и перемещения.

Работа постоянной силы равна произведению модуля вектора силы на модуль вектора перемещения и на косинус угла между ними.

Анализируя формулу , получаем:

1. α=0^о, то cos 0^о= 1, тогда А= F·S

2. α=90^о, то cos 90^о=0, тогда А=0

3. α=180^о, то cos 180^о= -1, тогда А=- F·S

4. 0^о < α < 90^о , то cos α >0 , тогда А >0

90^о < α < 180^о , то cos α< 0 , тогда А< 0

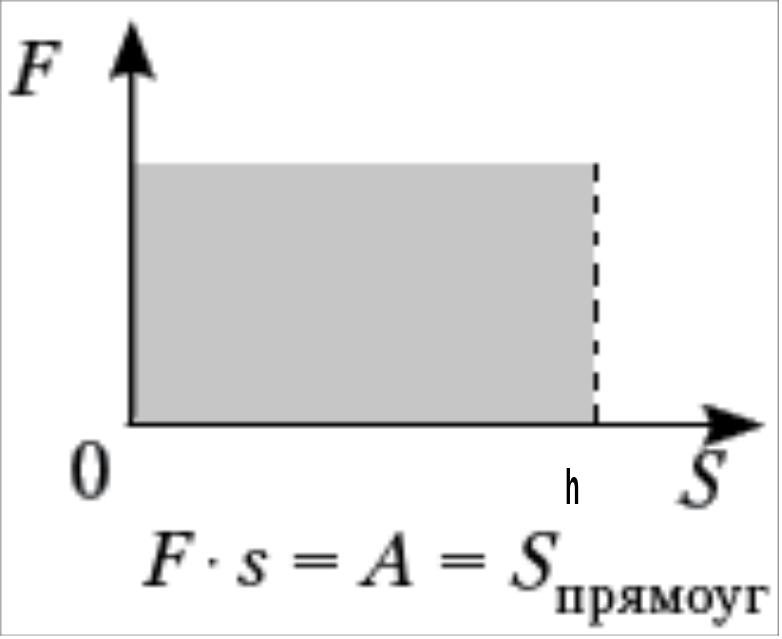
Изобразим графически зависимость модуля F_тяж oт модуля перемещения S.

Площадь заштрихованного прямоугольника численно равна работе, совершаемой постоянной силой при перемещении тела из одной точки в другую.

Пример: воду из колодца можно вычерпывать ведрами и насосом. Выполненная работа одинакова, а время выполнения работы разное. Поэтому человек использует механизмы, усиливающие его физические возможности ( автомобили, экскаваторы, подъемный кран). Для всякой машины можно определить ее производительность, то есть быстроту выполнения работы, называемую мощностью.

Мощностью называется отношение работы А к интервалу времени , за который эта работа совершена.

1 . Зная формулу мощности

давайте вспомним основную формулу для механической работы.

2. Пусть сила совпадает по направлению со скоростью тела. Запишем формулу работы этой силы.

3. При постоянной скорости движения, тело проходит путь определяемой формулой

4. Подставляем в исходную формулу мощности:

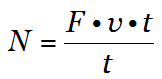
5. Получаем - мощность.

У нас получилась еще одна формула для расчета мощности, которую мы будем использовать при решении задач.

Единицы измерения. СИ: 1 = 1Вт 1 кВт; 1 МВт , ВНЕ: 1 л.с.≈735 Вт

Джеймс Уатт( 1736-1819)

Уатту принадлежит идея измерять механическую мощность в «лошадиных силах». Предложенная им единица мощности была весьма популярна, но в 1948 г. Генеральной конференцией мер и весов была введена новая единица мощности в международной системе единиц – ватт. Лошадиная сила – средняя работа за 1с, которую могла совершить ломовая лошадь, равномерно работающая целый день.

Мы изучаем механические системы. Какие они бывают? ( Приводятся примеры: два шара, тело и стол, просто мяч и др.) Таким образом, любые выделенные тела могут быть названы механической системой. Какие явления могут происходить в системе? ( тела в системе могут двигаться и взаимодействовать.) В качестве общей характеристики движения и взаимодействия тел в системе ученые ввели фундаментальную физическую величину – энергию. Энергия характеризует состояние движения и взаимодействия тел в системе.

Энергия – физическая величина, характеризующая способность тел совершать работу.

Тело или система тел, обладающая энергией, в состоянии совершить работу. Примеры: 1) движущийся по желобу шарик в состоянии передвинуть цилиндр; 2) сжатая пружина поднимает тело.

Как энергия тела зависит от скорости его движения?

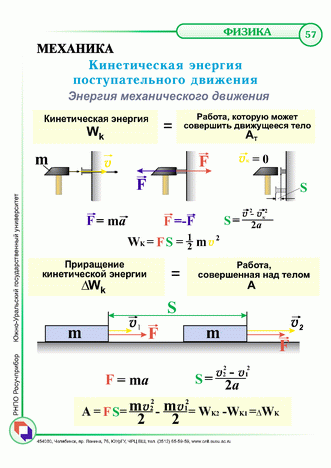
Тело движется прямолинейно под действием постоянной силы , совпадающей по направлению с вектором скорости тела. Поэтому . Так как , то α=0, . Из второго закона Ньютона

. Используя формулу , тогда .

Энергия, характеризующая движение тела, называется кинетической энергией.

Е_k=m∙v²/2

Учитывая эту формулу , получим следующее уравнение:

= или

= .

Это равенство выражает теорему об изменении кинетической энергии: изменение кинетической энергии тела( материальной точки) за некоторый промежуток времени равно работе, совершенной за это же время силой, действующей на тело.

Исторически первым сформировалось понятие кинетической энергии.

Это понятие было введено голландским физиком Гюйгенсом(1629 -1695), который называл кинетическую энергию по латыни: vis vitae – живая сила. Кинетическая – от греч. кinetikos – приводящий в движение.

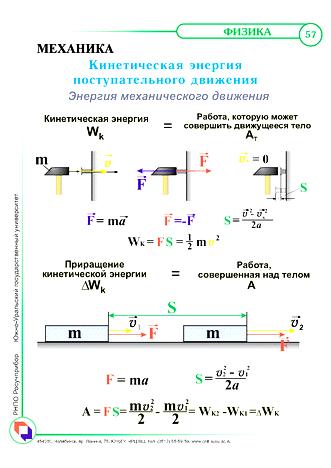
Особенности кинетической энергии:

1. кинетическая энергия зависит от скорости тела, следовательно, ее значение зависит от выбора системы отсчета;

2. кинетическая энергия – скалярная величина. По ее приращению можно судить о работе лишь результирующей ( равнодействующей) силы. Например: если автомобиль движется прямолинейно и равномерно, то прироста кинетической энергии нет , значит, работа результирующей силы равна нулю, хотя совершается работа двигателя, которая полностью компенсируется отрицательной работой сил сопротивления и трения.

3. кинетическая энергия системы тел равна сумме кинетических энергий тел, входящих в механическую систему.

Так как в природе нет одностороннего действия, а есть взаимодействие, то необходимо ввести еще один вид энергии- потенциальную энергию тела.

Потенциальная энергия – это энергия взаимодействия тел или частей одного тела.

Потенциальная энергия характеризует не любое взаимодействие тел, а лишь такое, которое описывается силами, называемыми потенциальными (сила тяжести - гравитационная, сила упругости). Эти силы отличает следующая особенность: - не зависят от скорости;- работа этих сил на любой замкнутой траектории равна нулю.

Потенциальной энергией тела в данном положении называется скалярная физическая величина, равная работе, совершенной потенциальной силой при перемещении из данного положения в нулевое.

Нулевое положение иначе называют уровнем отсчета потенциальной энергии. Для тела в поле притяжения Земли это, обычно, поверхность Земли. Для деформируемой пружины – нулевой уровень отсчета – ее нерастянутое состояние.

Вывод формулы потенциальной энергии тела, находящегося на высоте h :

.

Потенциальной энергией взаимодействия тела называют величину, равную произведению массы тела на ускорение свободного падения и высоту тела над Землей.