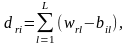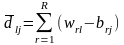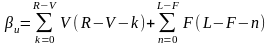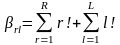- •3.2 Көппроцессорлы есептеу жүйелерінде бағдарламалық кешендер және деректер базасының массивтерін үлестіру есебінің тиімді алгоритмі, блок-схемасы
- •4 Үлестірілген және параллельді деректерді өңдеудің есебінің шешiмінің бағдарламалық қамтамасы
- •Қорытынды
- •Қолданылған әдебиеттер тізімі
- •Қосымша
- •Қосымшаның жалғасы
- •Қосымшаның жалғасы
- •Қосымшаның жалғасы
- •Қосымшаның жалғасы
- •Қосымшаның жалғасы
- •Қосымшаның жалғасы
- •Қосымшаның жалғасы
- •Қосымшаның жалғасы
- •Қосымшаның жалғасы
- •Қосымшаның жалғасы
3.2 Көппроцессорлы есептеу жүйелерінде бағдарламалық кешендер және деректер базасының массивтерін үлестіру есебінің тиімді алгоритмі, блок-схемасы
Дискретті бағдарламалаудың есептерінің алгоритмі мен талдау әдістері көрсеткендей, негізінде олар NP-толық есептер болып табылады және экспоненциялы есептеу қиындығын тудырады.
Белгілі алгоритмдер мен әдістерге қарағанда есептің қойылымын зерттеу және талдау жолымен, қасиеттері мен ерекшеліктеріне байланысты блокты-симметриялық есептерді шешудің тиімді алгоритмі құрылған және ұсынылған.
Көппроцессорлы есептеу жүйелерінде бағдарламалық кешендер және деректер базасының массивтерін үлестірудің есебінің тиімді алгоритмін қарастырамыз.
Алгоритмның сипаттамасы үшiн
келесi ұғымдарды анықтаймыз. Есептеу
жүйелерінде бағдарламалық кешендер
және деректер базасының массивтерін
үлестірудің есептерінде
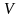 орындалатын модульдер саны мен
орындалатын модульдер саны мен
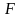 деректер базасынң массивтері алдын-ала
берілмесе, олар келесі теңдіктерден
анықталады
деректер базасынң массивтері алдын-ала
берілмесе, олар келесі теңдіктерден
анықталады
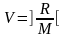 және
және
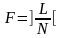 ,
мұндағы
,
мұндағы
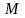 және
және
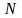 сәйкесінше модульдегі процедураның ең
үлкен мәні және деректер базасының
массивіндегі ақпараттық элементтердің
ең үлкен саны. Есептің шешімінің базисі
түсінігін анықтайық.
сәйкесінше модульдегі процедураның ең
үлкен мәні және деректер базасының
массивіндегі ақпараттық элементтердің
ең үлкен саны. Есептің шешімінің базисі
түсінігін анықтайық.
Анықтама 3.1
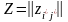 ішкі матрицасын, мұндағы
ішкі матрицасын, мұндағы
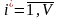 ;
;
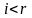 ;
;
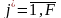 ;
;
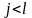 ,
,
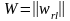 белгiлi бастапқы матрицада анықталған
есептің шешімінің базисі деп атаймыз.
белгiлi бастапқы матрицада анықталған
есептің шешімінің базисі деп атаймыз.
Базис ретінде түйінді ақпараттық элементтер немесе оларда қолданылатын деректерді өңдеу процедуралары қолданылады. Егер түйінді ақпараттық элементтер берілмесе, онда (В матрицасының жолдары және бағаналары) жобаның технологиялық талаптарына сәйкес қойылады.
Есептеу жүйелері мен кешендерінің түйіндеріне бағдарламалық және ақпараттық ресурстарды үлестірудің тиімді алгоритмін құру үшін келесі тұжырымда дәлелденген:
Есептеу жүйелерінің түйіндеріне
бағдарламалық модульдердің
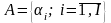 жиынын үлестіру бір түйінде орналасқан
жиынын үлестіру бір түйінде орналасқан
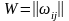 берілген матрица жолына логикалық
қосындысына, ал деректер базасының
массивтерінің
берілген матрица жолына логикалық
қосындысына, ал деректер базасының
массивтерінің
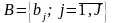 жиынын үлестіру берілген матрица
бағанының логикалық қосындысына сәйкес
келеді.
жиынын үлестіру берілген матрица
бағанының логикалық қосындысына сәйкес
келеді.
Бекітудің тұжырымдалған нәтижелері есептеу жүйелері мен кешендердегі үлестірілген және параллельді деректерді өңдеу алгоритмін тиімді құру үшін бағалау мен шешімді табу бағытын анықтауға мүмкіндік береді. Есептеу жүйелері мен кешендерінің түйіндеріне бағдарламалық және ақпараттық ресурстарды үлестіру есебінің шешімінің базисі ұғымын енгіземіз.
Анықтама 3.2
Есептеу жүйелерінің түйіндеріне А
жиынынан бағдарламалық модульдерін
және В жиынынан деректер базасының
массивтерін бастапқы үлестіру базис
болып табылады, ол
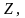 ішкі
матрицасын анықтайды, егер де әрбір
түйінде кем дегенде бір бағдарламалық
модуль және деректер базасының массивтері
орналасуы қажет.
ішкі
матрицасын анықтайды, егер де әрбір
түйінде кем дегенде бір бағдарламалық
модуль және деректер базасының массивтері
орналасуы қажет.
Анықталған Z ішкі матрицасын W матрицасының жолдары мен бағаналарын ауыстыру жолымен және оларды қайта нөмірлеу арқылы сол жақ жоғарғы бұрышта анықтауға болады, бұл есептің шешімін іздеуді анықтау және бағалауды қысқартады.
Сондықтан да, Z базисі есептің бастапқы шешімін анықтайды. Әдетте базисті есептің қойылымына сүйене қойылады немесе берілген өлшемдерге сәйкес анықталады. Есептеу жүйелері мен кешендерінің түйіндеріне бағдарламалық және ақпараттық ресурстарды үлестіру есебінің шешімі үшін Z базисінің жолдары мен бағандарының саны есептеу жүйесінің түйіндерінің санына тең, яғни, Z базисі төртбұрышты матрица болып табылады.
|
(3.2.1) |
|
(3.2.2) |
өлшемдерін базистарға кiрмейтiн жолдар (бағаналар) және базисқа кiретiн жолдармен (бағаналар) арасындағы қашықтықты атаймыз.
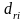 және
және
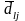 есептелген мәндері сәйкес
есептелген мәндері сәйкес
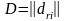 және
және
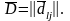 матрицаларына тең, ал олардың минимальды
мәндері есептеу жүйелерінің түйіндеріне
бағдарламалық модульдер мен деректер
базасының массивтерін бейнелеуін
(үлестіруін) анықтайды [50-52].
матрицаларына тең, ал олардың минимальды
мәндері есептеу жүйелерінің түйіндеріне
бағдарламалық модульдер мен деректер
базасының массивтерін бейнелеуін
(үлестіруін) анықтайды [50-52].
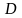 және
және
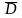 матрицаларын өзгерту процесінде
матрицаларын өзгерту процесінде
![]() және
және
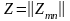 матрицаларымен тығыз байланысты, бұл
бейнелеу операциясынан кейінгі бастапқы
W матрицасының ағымдағы жағдайын
көрсетеді және олар базистік жолдарды
базиске кірмейтін жолдармен және
базистік бағандарды базиске кірмейтін
бағандармен логикалық қосу болып
табылады.
матрицаларымен тығыз байланысты, бұл
бейнелеу операциясынан кейінгі бастапқы
W матрицасының ағымдағы жағдайын
көрсетеді және олар базистік жолдарды
базиске кірмейтін жолдармен және
базистік бағандарды базиске кірмейтін
бағандармен логикалық қосу болып
табылады.
Алгоритм бірнеше итерациялық қатарлардан тұрады. Сондықтан оны итеративті бейнеленген алгоритмі деп анықтаймыз. Көппроцессорлы есептеу жүйелеріндегі процессорларға бағдарламалық модульдер мен деректер базасының массивтерін үлестірудің құрылған алгоритмі келесі операциялардан тұрады:
1 қадам. W матрицасын енгіземіз. Z базисін анықтау.
2 қадам. есептейміз және матрицасын құру.
3 қадам.
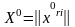 бастапқы мәнін және
бастапқы мәнін және
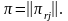 матрицаларын белгілеп қою.
матрицаларын белгілеп қою.
4 қадам.
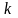 -шы
итерация.
-шы
итерация.
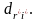 матрицасының
-шы
минимальды элементін табу. Ол үшін
шыққан мәндерді баған бойынша қосып,
оның ішіндегі минимальдысын табу керек.
Сол минимальды баған мен жолдың
қилысындағы минимальды элементті
белгілеу, оны
матрицасының
-шы
минимальды элементін табу. Ол үшін
шыққан мәндерді баған бойынша қосып,
оның ішіндегі минимальдысын табу керек.
Сол минимальды баған мен жолдың
қилысындағы минимальды элементті
белгілеу, оны
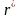 -ші
түйіндегі
-ші
түйіндегі
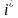 -ші
бағдарламалық модуліне орналастыру.
Егер бірнеше минимальды элементтер
кездессе, онда жол бойынша қосындысының
минимальдысын алу. Ал егер осындай
элементтердің қасиеттері бірнеше болса,
онда алдыңғы орналасқан элементті
аламыз.
-ші
бағдарламалық модуліне орналастыру.
Егер бірнеше минимальды элементтер
кездессе, онда жол бойынша қосындысының
минимальдысын алу. Ал егер осындай
элементтердің қасиеттері бірнеше болса,
онда алдыңғы орналасқан элементті
аламыз.
5 қадам. Х матрицасының элементтерін анықтау. Х айнымалысына қатысты шектерді тексеру, егер олар қанағаттандырса, 6-қадамға өту, әйтпесе 4-қадамға өту.
6 қадам.
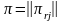 матрицасының
ағымдағы күйін жазып қою.
-ші
жолға қатысты
өлшемдерін қосу арқылы
матрицасының
ағымдағы күйін жазып қою.
-ші
жолға қатысты
өлшемдерін қосу арқылы
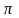 матрицасының жаңадан бейнелеу.
матрицасының жаңадан бейнелеу.
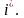 нөмірлі
жолды алып тастау .
нөмірлі
жолды алып тастау .
7 қадам. Келесі шартты тексеру:
есептеу жүйесінің түйіндеріне барлық
процедуралар үлестірілген бе? Жоқ болса,
онда келесі
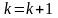 итерацияға
өту, әйтпесе 8-қадамға өту.
итерацияға
өту, әйтпесе 8-қадамға өту.
8 қадам.
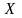 және
матрицаларының
құрамын толтыру.
және
матрицаларының
құрамын толтыру.
9 қадам. матрицасына қатысты есептеу және матрицасын құрастыру.
10 қадам. n-ші
итерация.
матрицасының n-ші
минимальды элементін табу. Ол үшін
шыққан мәндерді баған бойынша қосып,
оның ішіндегі минимальдысын табу керек.
Сол минимальды баған мен жолдың
қилысындағы минимальды элементті
белгілеу, оны
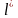 -ші
түйіндегі
-ші
түйіндегі
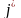 -ші
деректер базасына орналастыру. Егер
бірнеше минимальды элементтер кездессе,
онда жол бойынша қосындысының минимальдысын
алу. Ал егер осындай элементтердің
қасиеттері бірнеше болса, онда алдыңғы
орналасқанды таңдау қажет.
-ші
деректер базасына орналастыру. Егер
бірнеше минимальды элементтер кездессе,
онда жол бойынша қосындысының минимальдысын
алу. Ал егер осындай элементтердің
қасиеттері бірнеше болса, онда алдыңғы
орналасқанды таңдау қажет.
11 қадам.
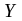 матрицасының элементтерін анықтау.
айнымалысына
қатысты шектерді тексеру, егер олар
қанағаттандырса, 12-қадамға өту, әйтпесе
10-қадамға өту.
матрицасының элементтерін анықтау.
айнымалысына
қатысты шектерді тексеру, егер олар
қанағаттандырса, 12-қадамға өту, әйтпесе
10-қадамға өту.
12 қадам.
матрицасының
ағымдағы күйін белгілеп қою.
-ші
бағанға қатысты
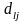 өлшемдерін қосу арқылы
матрицасының жаңадан бейнелеу.
нөмірлі
бағанды алып тастау.
өлшемдерін қосу арқылы
матрицасының жаңадан бейнелеу.
нөмірлі
бағанды алып тастау.
13 қадам. Келесі шартты тексеру: көппроцесорлық жүйе түйіндеріне барлық деректер базасының массивтері үлестірілген бе? Жоқ болса, онда келесі n=n+1 итерацияға өту, әйтпесе 14-қадамға өту.
14 қадам. Есептің шешімінің
қорытындысы:
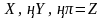 және
және
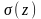 мақсат
функциясының мәндері.
мақсат
функциясының мәндері.
Жұмыстың енгізілген түсініктемелері мен тұжырымдамалары негізінде құрастырылған есептің шешімінің тиімді алгоритмі ұсынылған.
Итеративті бейнеленген алгоритмдері пайдалану арқылы есептерді шешу процесінде қадамдардың қажетті саны төмендегіге тең:
|
(3.2.3) |
мұнда
,
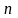 -
және
-
және
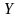 шешімдеріне сәйкес қалыптасу процесінде
итерациялар саны. Берілген есепті шешу
үшін «тармақ және шекара» әдісін
пайлалану арқылы қадамдар саны төмендегі
формула бойынша анықталады.
шешімдеріне сәйкес қалыптасу процесінде
итерациялар саны. Берілген есепті шешу
үшін «тармақ және шекара» әдісін
пайлалану арқылы қадамдар саны төмендегі
формула бойынша анықталады.
|
(3.2.4)
|
(3.2.1), (3.2.2) қатынастарын салыстыру «тармақ пен шекара» әдісіне қарағанда үлкен көлемді қойылған есептерді шешу үшін зерттелген алгоритмдердің полиномиалды күрделілік пен тиімділікті көрсетеді.
Итеративті бейнеленген алгоритмінің блок-схемасы 3.1-cурет көрсетілген.

3.1-cурет, 1-парақ. Итеративті бейнеленген алгоритмінің блок-схемасы

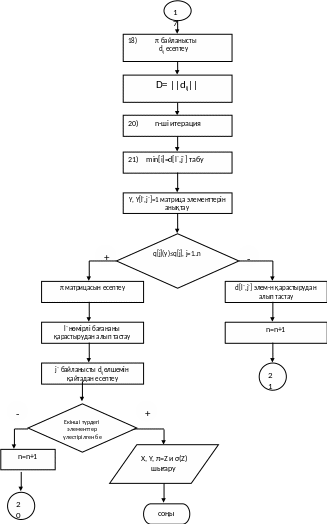
3.1-сурет, 2-парақ. Итеративті бейнеленген алгоритмінің блок-схемасы
Есептің шешімінің сандық
мысалын қарастырайық. Есептеу жүйелерінің
түйіндерінде қолданбалы бағдарламалар
мен деректер базасының массивтерін
үлестіру қажет деректер базасының
логикалық массивке ортақ сан минималдайтын
блок-схема синтез жасау керек. Есеп
келесі шарттармен анықталады: модуль
құрамында ұйғарынды процедуралар саны
3-ке тең, логикалық массивтер құрамында
ұйғарынды ақпараттық элементтер саны
4-ке тең. Модуль және логикалық массивтер
келесі формуламен анықталады:
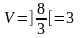 және
және
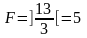 3.1-кестеде сол жақ жоғарғы бұрышта
бастапқы W
матрицасы ерекшеленген В базиспен
көрсетілген. 3.2-суретте өңделген
алгоритмді пайдаланып X
шешiмінiң қалыптастыру процесі көрсетілген.
3.1-кестеде сол жақ жоғарғы бұрышта
бастапқы W
матрицасы ерекшеленген В базиспен
көрсетілген. 3.2-суретте өңделген
алгоритмді пайдаланып X
шешiмінiң қалыптастыру процесі көрсетілген.
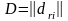 матрицасы 3.3-суреттегі қатынасты
пайдаланып анықталған [41].
матрицасы 3.3-суреттегі қатынасты
пайдаланып анықталған [41].
3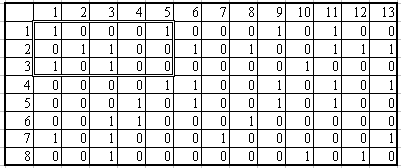 .1-
кесте - В базис матрицасымен ерекшеленген
.1-
кесте - В базис матрицасымен ерекшеленген
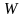 матрицасы
матрицасы
Бейнеленген процесс кестемен көрсетілген, онда итерация нөмері, -ның минимальды элементі анықталған, осыған байланысты модульдегі процедура нөмірі бейнеленеді. 3.1-суретте X және матрицалары да көрсетілген, оның құрамы шешімің іздеу базисімен, ал оң жақтағы және матрицаларында итеративті бейнелеу алгоритмін пайдаланумен анықталған.
3.3-суретте өңделген алгоритмді
пайдаланып Y
шешiмінiң қалыптастыру процесі көрсетілген.
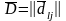 матрицасы 3.3-суреттегі қатынасты
пайдаланып анықталған. Бейнеленген
процесс кестемен көрсетілген, онда
итерация нөмері,
-ның
матрицасы 3.3-суреттегі қатынасты
пайдаланып анықталған. Бейнеленген
процесс кестемен көрсетілген, онда
итерация нөмері,
-ның
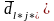 минимальды элементі анықталған, осыған
байланысты
деректер
базасында
түйін
нөмірі бейнеленеді.
минимальды элементі анықталған, осыған
байланысты
деректер
базасында
түйін
нөмірі бейнеленеді.
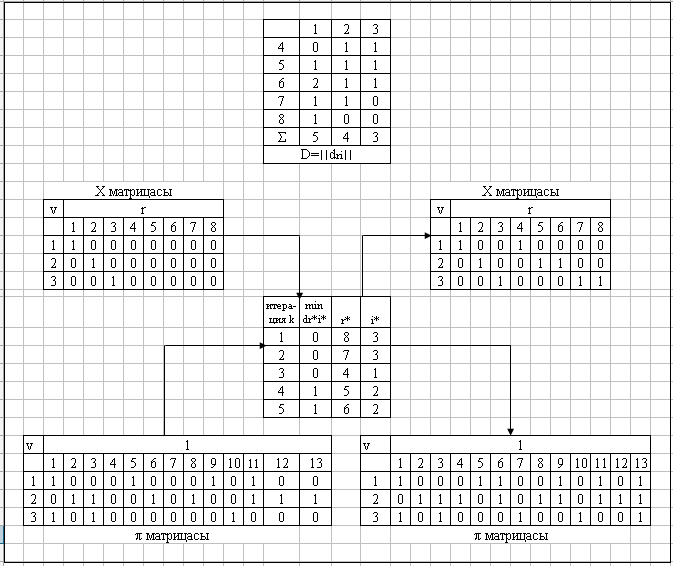
3.2-сурет. Итеративті бейнеленген алгоритмды қолданып Х шешiмін қалыптастыру процесі.
3.3-суретте Y
матрицасы көрсетілген, ол
шешімін
іздеу нәтижесінде алынған, ал оң жақтағы
X және
матрицаларында итеративті бейнелеу
алгоритмін пайдаланумен анықталған.
Сонымен қатар, Y
және
матрицалары итеративті бейнелеу
алгоритмін пайдаланумен анықталған.
матрицасы Z
мақсат функциясына сәйкес келеді, ол
деректерді өңдеудің бағдарламалық
модулі мен логикалық массивтің өзара
байланысын бейнелейді. Мақсат функцияның
тиімді мәні, алынған базис пен шарттардың
нәтижесінде
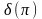 =
=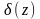 =7
тең.
=7
тең.
И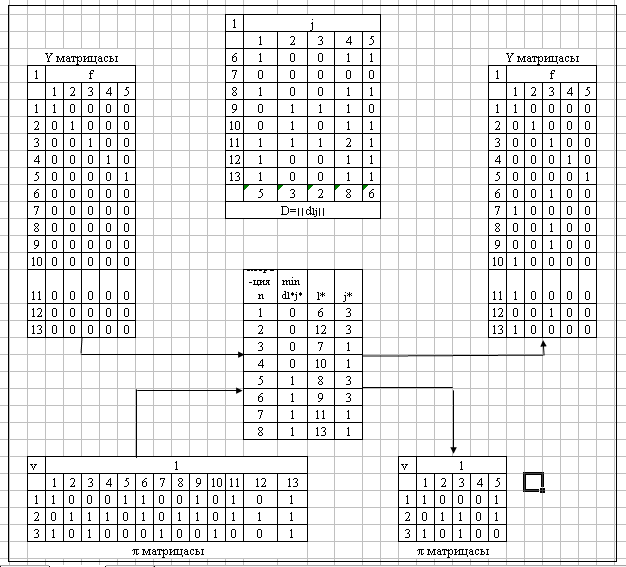 теративті
бейнеленген алгоритмды қолданып
блокты-симметриялық есептердің жеке
есептерін де шығаруымызға болады.
теративті
бейнеленген алгоритмды қолданып
блокты-симметриялық есептердің жеке
есептерін де шығаруымызға болады.
3.3-сурет. Итеративті бейнеленген алгоритмды қолданып Y шешiмін қалыптастыру процесі.
Блокты-симметриялық есептің
шешімін іздеу
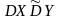 сүлбе
бойынша тура бағытта, керісінше
сүлбе
бойынша тура бағытта, керісінше
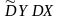 сұлба бойынша
кері бағытта да жүзеге асырылатынын
қарастырайық: Есеп
келесі шарттармен анықталады: модуль
құрамында ұйғарынды процедуралар саны
3-ке тең, логикалық массивтер құрамында
ұйғарынды ақпараттық элементтер саны
3-ке тең. Модуль және логикалық массивтер
келесі формуламен анықталады:
сұлба бойынша
кері бағытта да жүзеге асырылатынын
қарастырайық: Есеп
келесі шарттармен анықталады: модуль
құрамында ұйғарынды процедуралар саны
3-ке тең, логикалық массивтер құрамында
ұйғарынды ақпараттық элементтер саны
3-ке тең. Модуль және логикалық массивтер
келесі формуламен анықталады:
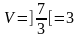 және
және
![]() .
3.2-кестеде сол жақ жоғарғы бұрышта
бастапқы
матрицасы
ерекшеленген В
базиспен көрсетілген. 3.4-суретте өңделген
алгоритмді пайдаланып X
шешiмінiң қалыптастыру процесі көрсетілген.
матрицасы 3.4-суреттегі қатынасты
пайдаланып анықталған.
.
3.2-кестеде сол жақ жоғарғы бұрышта
бастапқы
матрицасы
ерекшеленген В
базиспен көрсетілген. 3.4-суретте өңделген
алгоритмді пайдаланып X
шешiмінiң қалыптастыру процесі көрсетілген.
матрицасы 3.4-суреттегі қатынасты
пайдаланып анықталған.
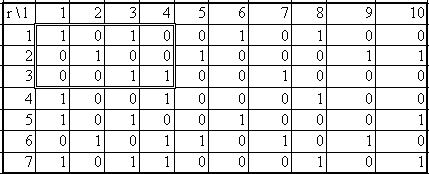 3.2-кесте
- В базиспен ерекшеленген
матрицасы
3.2-кесте
- В базиспен ерекшеленген
матрицасы
Б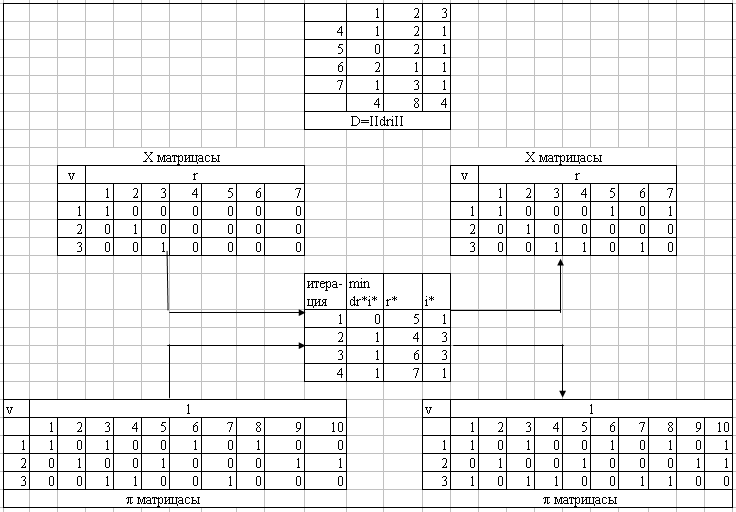 локты-симметриялық
есептің шешімін іздеу
сүлбе
бойынша тура бағытта орындалуын
қарастырамыз:
локты-симметриялық
есептің шешімін іздеу
сүлбе
бойынша тура бағытта орындалуын
қарастырамыз:
3.4-сурет. Итеративті бейнеленген алгоритмды қолданып X шешiмін қалыптастыру процесі.
3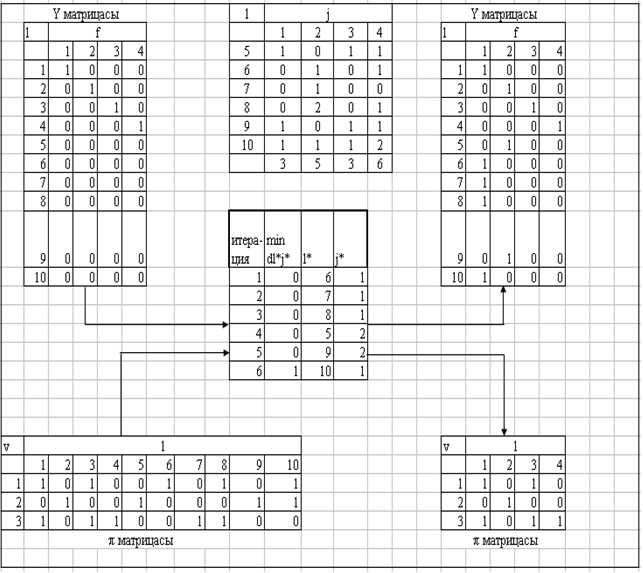 .5-сурет.
Итеративті бейнеленген алгоритмды
қолданып Y
шешiмін қалыптастыру процесі.
.5-сурет.
Итеративті бейнеленген алгоритмды
қолданып Y
шешiмін қалыптастыру процесі.
Мақсат функцияның тиімді мәні, алынған базис пен шарттардың нәтижесінде = =6 тең.
Блокты-симметриялық есептің шешімін іздеу сұлба бойынша кері бағытта да жүзеге асырылатынын қарастырайық:
3.6-суретте өңделген алгоритмді пайдаланып Y шешiмін табу процесі көрсетілген. матрицасы 3.6-суреттегі қатынасты пайдаланып анықталған. Бейнеленген процесс кестемен көрсетілген, онда итерация нөмері, -ның минимальды элементі анықталған, осыған байланысты деректер базасында түйін нөмірі бейнеленеді. 3.6-суретте Y матрицасы көрсетілген, ол Y шешімін іздеу нәтижесінде алынған, ал оң жақтағы Y және матрицаларында итеративті бейнелеу алгоритмін пайдаланумен анықталған. Бейнеленген процесс кестемен көрсетілген, онда итерация нөмері, -ның минимальды элементі анықталған, осыған байланысты модульдегі процедура нөмірі бейнеленеді. 3.7-суретте Y және матрицалары да көрсетілген, оның құрамы X шешімің іздеу базисімен, ал оң жақтағы X және матрицаларында итеративті бейнелеу алгоритмін пайдаланумен анықталған.
С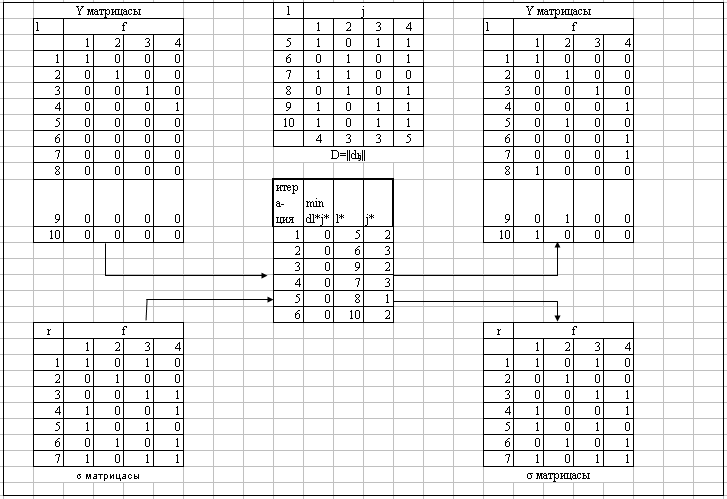 онымен
қатар, X
және
матрицалары итеративті бейнелеу
алгоритмін пайдаланумен анықталған.
матрицасы Z
мақсат функциясына сәйкес келеді, ол
деректерді өңдеудің бағдарламалық
модулі мен логикалық массивтің өзара
байланысын бейнелейді. Мақсат функцияның
тиімді мәні, алынған базис пен шарттардың
нәтижесінде
=
=6
тең.
онымен
қатар, X
және
матрицалары итеративті бейнелеу
алгоритмін пайдаланумен анықталған.
матрицасы Z
мақсат функциясына сәйкес келеді, ол
деректерді өңдеудің бағдарламалық
модулі мен логикалық массивтің өзара
байланысын бейнелейді. Мақсат функцияның
тиімді мәні, алынған базис пен шарттардың
нәтижесінде
=
=6
тең.
3.6- сурет. Итеративті бейнеленген алгоритмды қолданып Y шешiмін қалыптастыру процесі.
3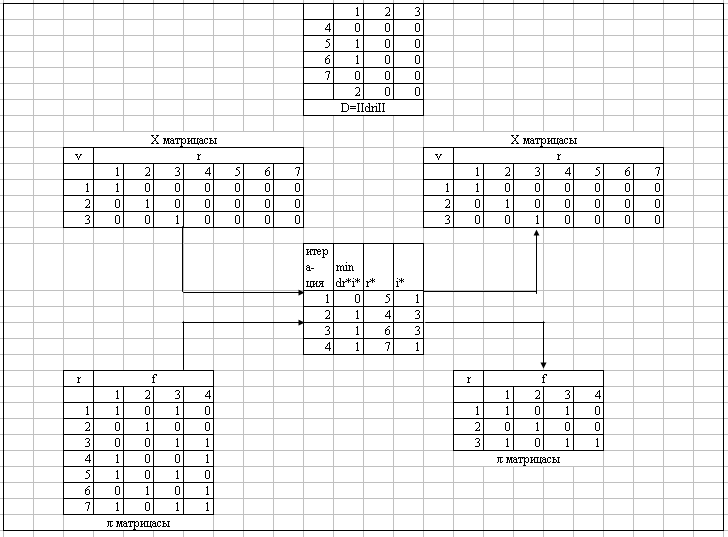 .7-сурет.
Итеративті бейнеленген алгоритмды
қолданып Y
шешiмін қалыптастыру процесі.
.7-сурет.
Итеративті бейнеленген алгоритмды
қолданып Y
шешiмін қалыптастыру процесі.
Бұдан шығатыны берілген W
матрицасына қарағанда X
және Y
айнымалылары симметриялы және
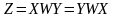 функциясы
солдан оңға, сол сияқты керісінше
анықталады.
функциясы
солдан оңға, сол сияқты керісінше
анықталады.