12. Структура аналитико-статистических моделей полей сигналов. Переменные модели..

Аналитико-стат модель – это статистическая с притягиванием теоретических данных (представление об объекте).

Переменными модели являются ее информативные признаки, отображающие наличие у объекта существенных для решения пользовательских задач свойств, и факторы условий, задаваемые вне модели и характеризующие условия существования формального представления об объекте.

Статистические модели полей излучения различных природных образований строится в виде многомерных условных плотностей распределения P{ /W} вектора информативных признаков ={X₁,X₂...X_i...X_n}, где W обозначает совокупность факторов условий.

Переменными модели являются «функции» - информативные признаки моделируемых объектов и «аргументы» - переменные, от которых зависят функции – признаки. Характер зависимости может выражаться аналитически или статистически, при этом некоторые признаки могут задаваться аналитически, а другие – статистически.

13. Форма представления аналитико-статистических моделей. Конечномерные сечения многомерных моделей. Построение конечномерных сечений многомерных моделей

ФОРМА ПРЕДСТАВЛЕНИЯ

Аналитико-статистические модели представляют обычно в виде аналитических зависимостей и локальных баз данных (вспомогательных информационных массивов), позволяющих получать значения признаков при заданных условиях; информационных массивов признаков (или их статистических параметров) при заданных условиях (пользовательские таблицы); информационных массивов признаков при заданном наборе условий, и интерполяционных (экстраполяционных) формул, так, что получение значений признаков при промежуточных условиях обеспечивается инерполяцией (экстраполяцией) заданного вида; аналитических зависимостей со случайными параметрами и правил, по которым можно генерировать случайные последовательности значений параметров или значений их статистических параметров; аналитических зависимостей со случайными параметрами и значений их статистик в зависимости от других условий (например, географических координат); в общем случае – многомерной условной плотности распределения признаков для различных диапазонов факторов условий.

Конкретная форма представления определяется внешними по отношению к модели требованиями пользователя. Для разработчика модели, работающего в определенной тематической области, целесообразно сформировать собственное представление, исходя из которого он сможет удовлетворять пользовательские запросы различного содержания («у меня есть модель»).

КОНЕЧНОМЕРНЫЕ СЕЧЕНИЯ ИЛИ ПРЕДСТАВЛЕНИЯ

Высокие размерности признаковых пространств статистических моделей затрудняют работу с ними, поэтому там, где это возможно, вместо полных многомерных представлений моделей используются их конечномерные сечения, описывающие проекции функций P{ /W} на пространства меньшей размерности. Простейшим случаем таких проекций являются двумерные представления. Сечения модели строятся таким образом, чтобы векторы информативных признаков объектов, описываемых этой моделью, с определенной вероятностью  принадлежали области сечения. Для одномерных сечений вероятность признаку принадлежать интервалу (X1,X2) будем обозначать . Величины  и  называют также вероятностнм содержанием соответственно одномерного или многомерного интервала.

Если информативные признаки статистической модели независимы (при нормальном законе распределения достаточным условием этого является их некоррелируемость), условную многомерную плотность распределения P{ /W} можно представить в виде

P{ /W} = P{X1/W}P{X2/W}...P{Xi/W}...P{Xn/W}, (1.4)

где P{Xi/W} - одномерные законы распределения признаков.

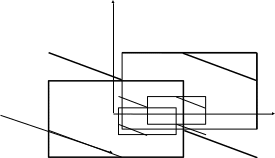
Сечением многомерной модели (1.4) в пространстве некоррелированных признаков размерности n будет n- мерный гиперпараллелепипед (рис.1.1, 1.2).

Вероятность события, состоящего в том, что выборочные значения признаков попадают внутрь этого гиперпараллелепипеда будет иметь вероятность  = ()n, где  - вероятность попадания выборочных значений каждого признака Xi в интервал (Xi1,Xi2), отложенный на соответствующей оси. В этом случае центр доверительного интервала будет лежать в точке M с координатами M(M1,M2,...Mi,...Mn)

Для одномерных нормальных распределений полностью определено вероятностное содержание k интервалов (Mp  kp). Как следует из таблиц нормального распределения, при k= 1 1 = 0,68, при k= 2 2 = 0,95, при k= 3 3 = 0,9973.

Если распределение значительно отличается от нормального и известны только одномерные гистограммы признаков, полученные по выборке, координаты углов многомерного гиперпараллелепипеда рассчитываются следующим образом.

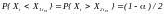(1.5)

Сечением многомерной модели (1.1) в пространстве коррелированных признаков размерности n в предположении нормального распределения будет n- мерный гиперэллипсоид, для двумерного случая называемый эллипсом рассеяния (рис.1.3).

Основное свойство эллипсов рассеяния состоит в том, что в предположении равномерного распределения вероятностей в них ковариационная матрица такого распределения совпадает с ковариационной матрицей исходного распределения.

Вероятностное содержание эллипса рассеяния рассчитывается по формуле

P =

= =1-exp(-2/2) (1.6)

X_l

X_l21

X_l22

X_l12

X_l11

X_p

X_p11 X_p12 X_p22 X_p21

Рис. 1.1. Проекция многомерной плотности распределения на двумерное пространство некоррелированных признаков

X_k

X_l

X_p

Рис. 1.2. Проекция многомерной плотности распределения на трехмерное пространство некоррелированных признаков

X_m X_m

X_f^



M_m

O

b

a

M_f X_f

Рис.1.3. Проекция многомерной нормальной плотности распределения на двумерное пространство коррелированных признаков (эллипс рассеяния).

14.Пространственные спектральные модели как пример аналитико-статистических моделей полей сигналов. Структура пространственной спектральной модели. Информативные признаки пространственных спектров (энергетические, метрические, топологические, структурно-зональные).

Построение математической модели означает формализацию представлений об объекте-прототипе в виде математического аппарата модели и входящих в нее переменных. Переменными модели являются ее информативные признаки, отображающие наличие у объекта существенных для решения пользовательских задач свойств, и факторы условий, задаваемые вне модели и характеризующие условия существования формального представления об объекте (СМ. Л1).

Как следует из анализа задач, для решения которых используется двумерная пространственная спектральная модель, ее структура должна обеспечивать как решение задач распознавания различных классов природных объектов по их пространственным спектрам, так и восстановление двумерных массивов .

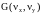При разработке пространственной спектральной модели (ПСМ) различных природных образований можно использовать статистический метод моделирования, заключающийся в описании трехмерной фигуры двумерного пространственного спектра путем задания многомерной условной плотности распределения информативных признаков {X_i}, рассчитываемых как функционалы от . Статистическая пространственно-спектральная модель содержит оценки законов распределения информативных признаков плоской фигуры сечения пространственных спектров (ПС), а также энергетических признаков, характеризующих распределение энергии внутри фигуры ПС для различных спектральных диапазонов. Такая система информативных признаков может успешно применяться при решении задач классификации природных образований по типам. На последующих этапах, по мере накопления исходных материалов, стало возможно уточнить полученные статистические оценки и перейти к аналитическим описаниям формы трехмерной фигуры ПС для различных природных образований; при этом параметры аналитического описания ПС могут являться информативными признаками, получаемыми с использованием статистического метода моделирования или пространственными характеристиками (размерами) моделируемых объектов. Все информативные признаки, используемые при построении статистической модели, могут быть получены из аналитических представлений ПС, что обеспечивает непротиворечивость обоих подходов к построению модели.

Учитывая многобразие форм ПС, соответствующих различным природным образованиям, можно заключить, что создание единой аналитической модели для всех типов ПС нецелесообразно. Как следует из результатов исследований (примеры ПС морфологически одногодных объектов суши и атмосферы приведены на рис.1.5, 1.6), сечения ПС представляют собой либо достаточно простые геометрические фигуры (круг, эллипс, астроиду, овал Кассини и т.п.), либо, для многосвязных спектров, могут быть описаны их сочетаниями. С другой стороны, в формировании текстуры изображения в пределах поля обзора бортовой аппаратуры могут участвовать одна, две или более компонент природной среды, образующих морфологически однородное природное образование, пространственный спектр которого может быть как односвязным, так и многосвязным. Поэтому при разработке ПСМ можно применить многомодельный подход, успешно развиваемый при создании моделей полей излучения в целом.

На рис.2.7 приведена классификация форм двумерных ПС, типичных для различных природных объектов, проведенная по результатам обработки больших массивов экспериментальных данных.

Рис.1.7. Классификация форм двумерных пространственных спектров

Применение этого подхода для описания ПС предполагает формирование J "простых" подмоделей, каждая из которых описывает односвязную фигуру, являющуюся либо ПС какого-либо класса природных образований, либо элементом ПС; модель ПC каждого конкретного типа морфологически однородного природного образования 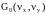представляется как совокупность всех подмоделей , для которых из математического аппарата модели {П} выбирается совокупность операций над ними П₀ для различных конкретных случаев

(1.7)

С учетом этого ПСМ должна описывать отображение в пространство информативных признаков {X_i} всех подмоделей , моделей различных классов , а также правила сочетания отдельных подмоделей П₀ для каждого варианта факторов условий.

С учетом необходимости разработки единой структуры для статистической и аналитической ПСМ, в качестве информативных признаков двумерных ПС можно выбрать :

- топологические признаки Т{...} (число независимых компонент K, число Эйлера E, число дыр H в плоской фигуре ПС);

- геометрические признаки {...} (отношение формы Ф, отношение аспекта А, отношение толщины Т);

- энергетические E{...} (мощность кольцевых составляющих пространственного спектра g(), наклоны одномерных сечений a, полученные по различным направлениям);

- аналитическую функцию, описывающую форму плоской фигуры ПС, f(...), заданная в полярных или декартовых координатах.

Геометрические признаки рассчитываются по формулам:

- отношение толщины

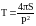; (1.8)

- отношение формы

; (1.9)

- отношение аспекта

, (1.10)

где S - площадь; P - периметр; L_max, L_min -величины максимальной и минимальной вытянутости двумерного ПС, рассчитываемые не по отдельным элементам, а по всех фигуре независимо от ее сложности и связности.

При разработке ПСМ практически удобно ориентироваться на представление пространственных спектров в виде функции полярных координат 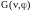, где

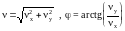. (1.11)

Для полей яркости большинства природных образований спектр характеризуется степенным уменьшением спектральной плотности и допускает аппроксимацию функцией вида

если

если

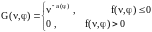, (1.12)

где

a() - параметр наклона ПС;

f(,) - функция, описывающая форму ПС, заданная в полярных координатах.

Параметр наклона для каждого направления рассчитывается по методу наименьших квадратов как параметр логарифмически линейной аппроксимации ПС

, (1.13)

где A - нормировочный множитель.

К энергетическим признакам ПСМ относятся:

- среднее по всем направлениям значение параметра наклона a

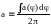(1.14)

- наклоны a_max и a_min одномерных сечений ПС по максимальным и минимальным осям спектра, рассчитываемые как параметры логарифмически-линейной аппроксимации ПС по направлениям максимальной и минимальной вытянутости ПС:

, (1.15)

, (1.16)

где

(max), (min) - углы, соответствующие направлениям максимальной и минимальной вытянутости ПС;

C_x, C_n - константы;

- наклоны a_j, a_jmax, a_jmin, рассчитываемые по формулам (1.15,1.16) для каждой компоненты многосвязных ПС.

Мощность кольцевых составляющих пространственных спектров g() в диапазоне пространственных частот  рассчитывалась по формуле:

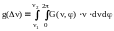, (1.17)

где

G(,) - значение мощности двумерного ПС в полярных координатах;

=(₁, ₂).

Мощности кольцевых составляющих рассчитываются только для всего спектра, независимо от его связности.

Математический аппарат модели может быть построен исходя из следующих соображений.

Рассмотим три типа наблюдаемых природных объектов:

- простая текстура, имеющая спектр одного из типов {G_j};

- составная текстура, для которой можно четко выделить составляющие компоненты, являющиеся простыми текстурами;

- сложная текстура, для которой составляющие компоненты выделить нельзя.

Для первого и третьего случаев аналитическое описание ПС сводятся к выбору подмодели G_j, набора простых функций формы, описывающих эту подмодель в случае, если спектр G_j составляется из простых фигур и описанию математических операций, обеспечивающих учет конкретных условий наблюдения, то есть преобразования этих фигур.

Для второго случая нужно рассмотреть варианты, когда компоненты принадлежат одному высотному ярусу и когда они принадлежат разным ярусам. В первом из них поле яркости ситуации B_s можно представить в виде суммы

B_s(x,y) = B₁(x,y) + B₂(x,y) + ...+ B_j(x,y) + ... , (1.18)

где B_j(x,y) - поле яркости j-той компоненты.

Для второго варианта

B_s(x,y) =B_j-1(x,y)(*)B_j(x,y) , (1.19)

где

B_j(x,y) - нормированное поле яркости j-той высотной компоненты;

B_j-1(x,y) - поле яркости уходящего излучения на верхней границе (j-1)-й компоненты;

(*) обозначает операцию свертки.

После преобразования Фурье выражение (1.18) преобразуется к виду

F[B_s(x,y)] =F[B₁(x,y)] + F[B₂(x,y)] + ... + F[B_j(x,y)] + ... , (1.20)

а выражение (1.19) - к виду

F[B_s(x,y)] =F[B₁(x,y)]F[B₂(x,y)]...F[B_j(x,y)]... , (1.21)

Соответственно, ПС для первого случая будет представлять собой сумму ПС отдельных компонент и их взаимных спектров

, (1.22)

где G_ij(_x,_y) - взаимный спектр i и j компонент.

Для независимых компонент взаимные спектры будут равны нулю на всех ненулевых частотах и могут не учитываться.

Для второго случая ПС будет выражаться как произведение ПС отдельных компонент

. (1.23)

Таким образом, совокупность правил сочетания П₀ имеет вид:

, если комопненты принадлежат

одному высотному ярусу;

, если комопненты принадлежат

разным высотным ярусам.

(1.24)

При компоновке ПС сложной формы для составных текстур из простых элементов необходимо иметь в аппарате ПСМ следующие операции 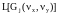над простыми фигурами :

- масштабирование M_ в частотной плоскости

G_j(_x,_y)=G_j( M__x, M__y);

- масштабирование M_G значений спектральной плотности

G_j(_x,_y)= M_GG_j(_x,_y);

- сдвиг относительно начала координат

G_j(_x,_y)= G_j(_x - _xj, _y - _yj);

- поворот на угол _j

G(,)=G(,-_j).

В состав факторов условий существования ПСМ как формального представления о двумерных пространственных характеристиках фона входят параметры, влияющие на процесс формирования текстуры изображения и ее пространственного спектра. Исходя из этого в состав факторов условий целесообразно включить:

- объективные характеристики природной среды, влияющие на геометрическую форму элементов с различными оптическими свойствами и контрасты яркости в различных диапазонах (мешающие параметры);

- параметры, оказывающие прямое воздействие на формирование ПС изображения и связанные со способом получения исходных изображений, используемых для построения модели (управляющие параметры)

К первому типу относятся:

О_ф - тип наблюдаемого природного объекта;

В_осв - параметры условий освещения (дата, время, зенитный угол Солнца, угол рассеяния);

 - метеорологические параметры (балл облачности, высота верхней границы, вид и разновидность облачности, линейные размеры облачных элементов).

Действительно, О_ф полностью определяет всю совокупность элементов наблюдаемой сцены, а значит и их оптические свойства и повторяемости. Изменение условий освещения влияет на контрасты элементов текстуры, что особенно важно для рельефов подстилающей поверхности и облачности с большими перепадами высот. Это проявляется как явление "дефицита пространственных частот" для ситуаций с облачностью. Метеорологические параметры непосредственно влияют на макротекстуру сцен с облачностью, а также на дисперсию результирующего поля яркости в каком бы диапазоне оно ни наблюдалось. Ко второму типу факторов условий относятся:

U - параметры системы наблюдения (район, координаты точки наведения, высота носителя, зенитный угол линии визирования);

 - параметры бортовой аппаратуры (тип, спектральный диапазон, частотный диапазон, угловые размеры мгновенного поля зрения, угловые размеры поля обзора);

 - параметры, используемые при обработке (расситываемые признаки, размеры обрабатываемых фрагментов, пороговые уровни, объемы выборок).