Иррационал теңсіздіктер
Функциясы радикалға тәуелді теңсіздіктерді иррационал теңсіздіктер деп атайды.
;
(1)
түріндегі теңсіздіктерді қарастырайық. Иррационал теңсіздіктерді шешкенде теңдеудің екі бөлігін дәрежелейді, одан бөгде түбір шығуы мүмкін. Теңсіздіктің екі жағы теріс болмаған жағдайда оларды квадраттап, одан арифметикалық түбір табамыз.
теңсіздігі үшін
және
болуы қажетті. Осы шарттарды ескеріп,
теңсіздіктің екі жағын квадраттағанда
олармен мәндес теңсіздіктер жүйесін
аламыз:
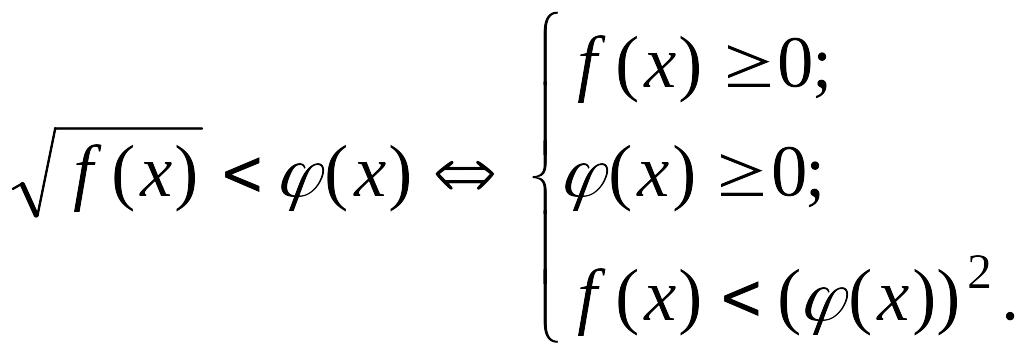(2)
теңсіздігінің
оң жағының таңбасы туралы еш нәрсе
айтылмаған. Сондықтан екі жағдайды
қарастырамыз: 1)
2)
.
Бірінші
жағдайда
теңсіздігі
және
болатын барлық
-тер
үшін орындалады.
Екінші жағдайда теңсіздіктің екі бөлігі де теріс емес екенін ескеріп, теңсіздікті квадраттайды, берілгенге мәндес теңсіздіктер жиынтығын алады. Демек,
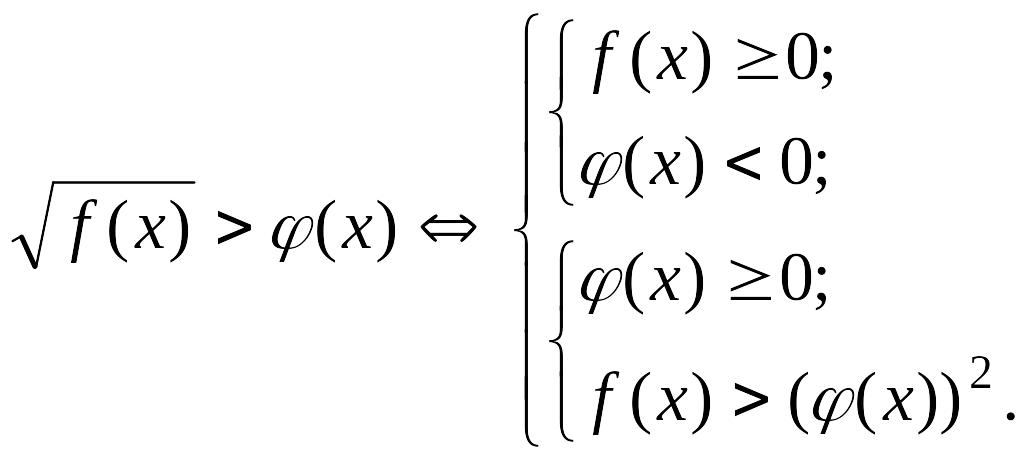(3)
теңсіздігінің шешімдер жиынын алу үшін жиынтықтың әр жүйесінің барлық шешімін біріктіру керек. пен –тің мүмкін мәндер аймағының барлық -і үшін
,
(4)
теңсіздіктері анықталған. Бұлар теңсіздіктің екі жағын дәрежелеу арқылы шешіледі.
(5)
теңсіздігі
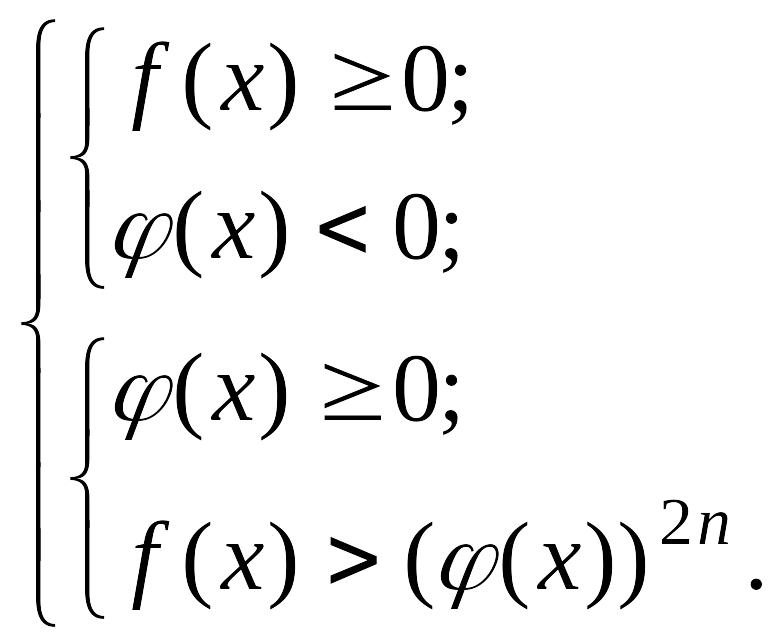(6)
теңсіздіктер жүйесінің жиынтығымен мәндес.
(7)
теңсіздігі
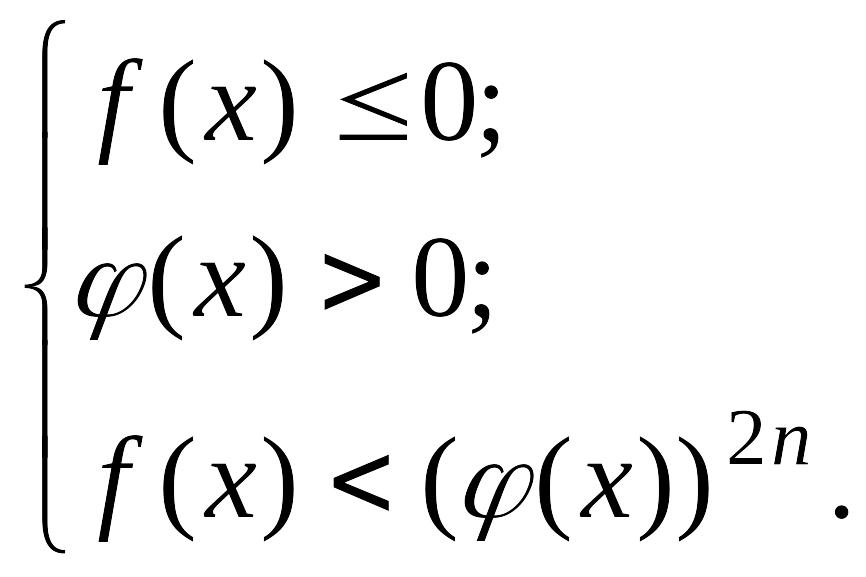(8)
теңсіздіктер жүйесімен мәндес. Иррационал функциялардың анықталу аймағын табудың мәні зор. Әсіресе, теңсіздіктің екі жағының таңбасын алдын-ала зерттегенде оның ерекше мәні бар.
1-мысал.
–
теңсіздігін шешу керек.
Шешуі:
Теңсіздік
болғанда анықталады, не
.
Теңсіздіктің екі жағын квадраттап,
түрлендірсек,
теңдеуінің түбірлері
демек,
теңсіздігі
және
.
Берілген теңсіздіктің шешімі
.
2-мысал.
теңсіздігін шешу керек.
Шешуі:
Теңсіздік
не
және
не
болғанда анықталады.
теңдеуінің түбірлері
теңсіздігі
болғанда дұрыс орындалады.Берілген
теңсіздіктің екі жағын квадраттап
бұдан
Сонымен,
3-мысал.
теңсіздігін шешу керек.
Шешуі:
Берілген теңсіздікті
түрінде жазамыз. Сол жағының анықталу
аймағы
Анықталу аймағының барлық нүктелерінде
бұл функция теріс емес (себебі арифметикалық
түбір алынады).
болғанда оң жағы теріс, сондықтан
берілген теңсіздік
-тің
кесіндісінде жатқан барлық мәндері
үшін теңсіздік дұрыс.
Көрсеткіштік теңсіздіктер
Айнымалысы
дәреже көрсеткішінде болатын теңсіздіктерді
көрсеткіштік теңсіздік деп атайды.
Көрсеткіштік теңсіздіктерді шешу үшін
көрсеткіштік функцияның қасиеттері
қолданылады.
болғанда бұл функция өспелі,
болғанда кемімелі.
Теңсіздіктердің аталған қасиеттері негізінде
(9)
теңсіздігі пен -тің анықталу аймақтарының қиылысуында ( болғанда) (10) теңсіздігімен мәндес, ал болғанда (11) теңсіздігімен мәндес. Дәл осылайша
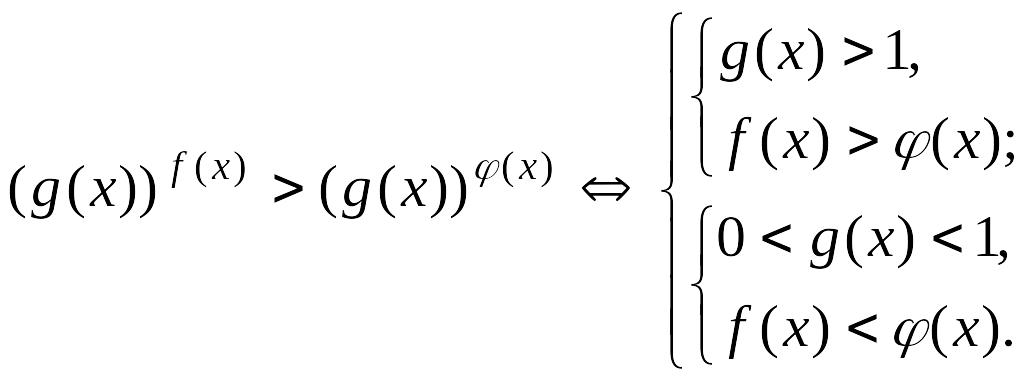(12)
(13)
теңсіздігін қарастырайық.
Егер
,
онда
теңсіздіктің шешімі кез келген сан.
Егер болса, онда берілген теңсіздік болғанда
(14)
теңсіздігімен , ал
болғанда
(15) теңсіздіктерімен мәндес.
Егер
болса, онда
сан теңсіздігін аламыз.
(16) теңсіздігі
болғанда шешімі жоқ, ал
болғанда мына
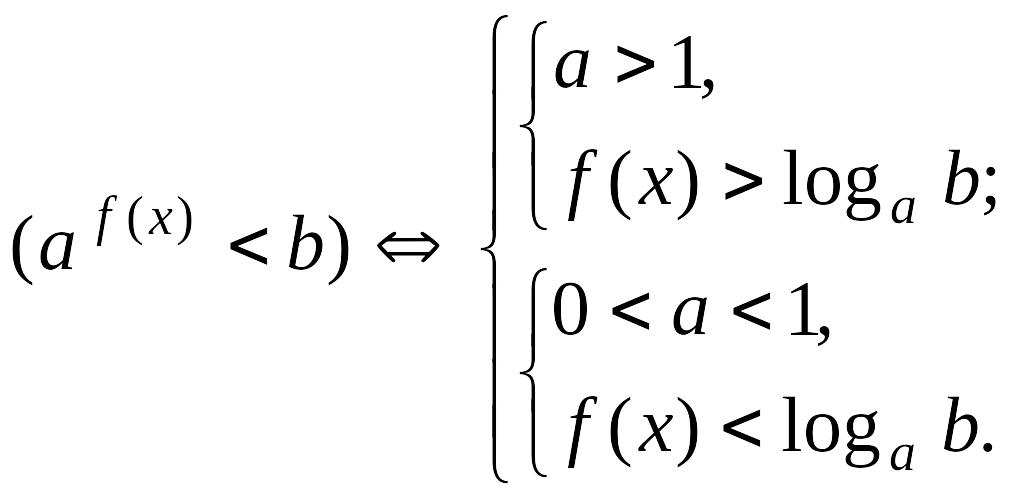(17)
теңсіздіктержүйесінің жиынтығымен мәндес.
(не
нөлден кем)
(18)
түріндегі
теңсіздік
(19) белгілеп орнына қоюдың көмегімен
квадрат теңсіздікке келтіріледі.
(не
нөлден кем) (20).
7-мысал.
теңсіздігін шешейік.
Шешуі:
Теңсіздікті
басқаша жазып түрлендірейік:
Бұдан
Сонымен, теңсіздіктің шешуі
8-мысал.
теңсіздігін шешу керек.
Шешуі:
Теңсіздіктің
екі бөлігін де
өрнегіне бөліп,
теңсіздігін аламыз. Бұдан
Сонымен,
9-мысал.
теңсіздігін шешу керек.
Шешуі:
Теңсіздік
не
болса, анықталады.
,
.
Берілген теңсіздікті квадраттаймыз.
Теңсіздіктің
шешуі
10-мысал.
теңсіздігін шешу керек.
Шешуі:
Берілген теңсіздікті түрінде
түрінде жазамыз.
жаңа айнымалы ендіреміз, сонда теңдеу
түрінде жазылады.
теңдеуінің түбірлері
теңсіздігі
болғанда орындалады. Бұдан
–нөлден
кіші және нөл мән қабылдамайды. Сондықтан
-тен
Екіншіден
.
кез келген сан.
11-мысал.
теңсіздігін шешу керек.
Шешуі:
болғанда берілген теңсіздік анықталады.
Бәрін 2 негізіне келтірсек
(теңсіздіктің екі бөлігін де
–ке
мүшелеп бөлдік).
жаңа айнымалы ендірсек, онда соңғы
теңсіздік
түріне келеді.
болғандықтан
түбірлері
не
теңсіздігінен
десек
Бұдан
Егер
бар болса, онда
яғни
