3. Бір айнымалысы бар сызықты теңсіздіктер
(1)
түріндегі теңсіздікті бір айнымалысы бар сызықты теңсіздік деп атайды.
(1) теңсіздікті мәндес теоремаларына сүйеніп
(2)
түрінде
жазуға болады. Егер
болса, онда
.
Бұл жағдайда (2) теңсіздік айнымалының
аралығындағы кез келген мәнін қабылдайды.
Егер
болса, онда (2) теңдік
түрінде шешіледі. Демек, айнымалының
аралығынан алынатын кез келген мәні
теңсіздікті қанағаттандырады. Егер
,
болса, онда (2) теңсіздік
–тің
кез келген мәнін қанағаттандырады, яғни
теңсіздіктің
–гі
шектеусіз көп шешуі болады. Егер
,
болса, онда (2) теңсіздіктің шешуі
болмайды. (1) сияқты теңсіздікті шешу
үшін (2) оны түріне келтіреді. (2) теңсіздіктің
екі жағын айнымалының коэффициентіне
бөледі. Егер
болса, онда
немесе
теңсіздіктер дұрыс па соны тексеру
керек. Біріншісінде
болса, екіншісінде
болса ғана шешуі бар.
1-мысал.
теңсіздікті шешу керек.
Шешуі: Алдымен теңдеулерді бүтін коэффициентті теңдеуге келтіреміз:
не
,
,
Теңсіздіктің
шешімі
– аралығы.
2-мысал.
теңсіздікті шешу керек.
Шешуі: Теңсіздіктің екі бөлігін 3-ке көбейтеміз, сонда
бұдан
,
,
Теңсіздіктің
шешімі
аралығы.
3-мысал.
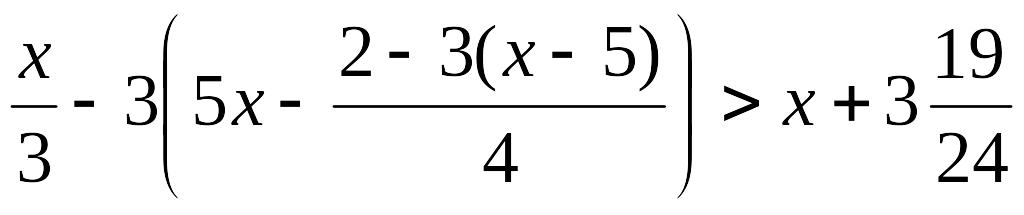теңсіздігін шешу керек.
Шешуі: Алдымен жақшаны ашайық:
,
Теңсіздіктің
шешімі
аралығы.
Сызықты теңсіздіктер жүйесі
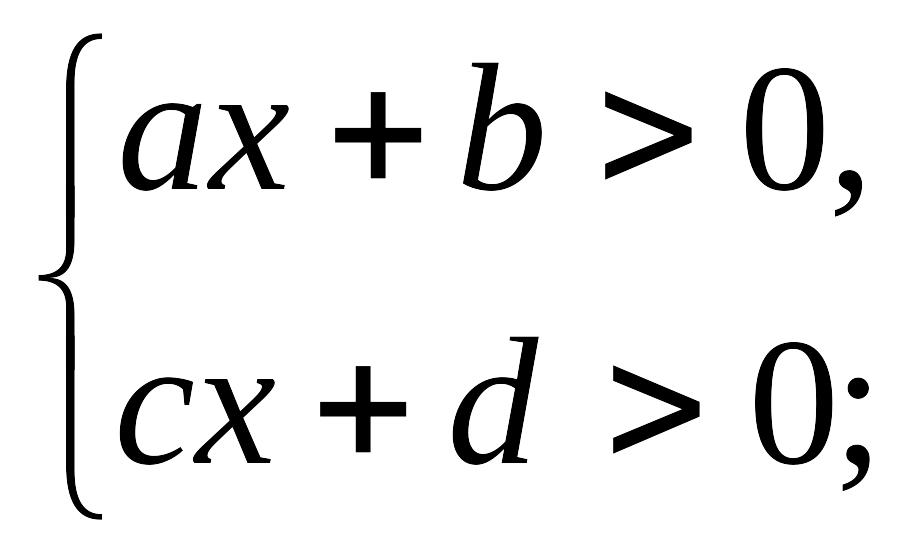
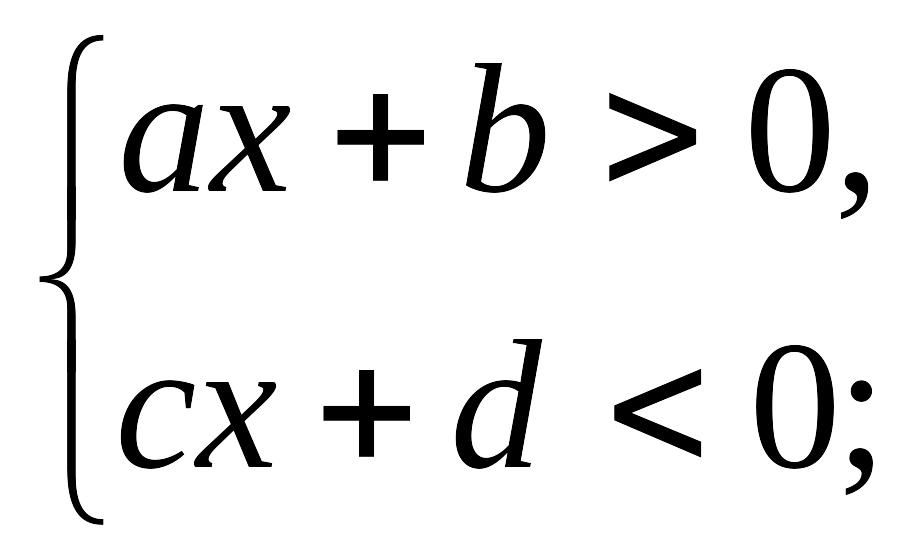
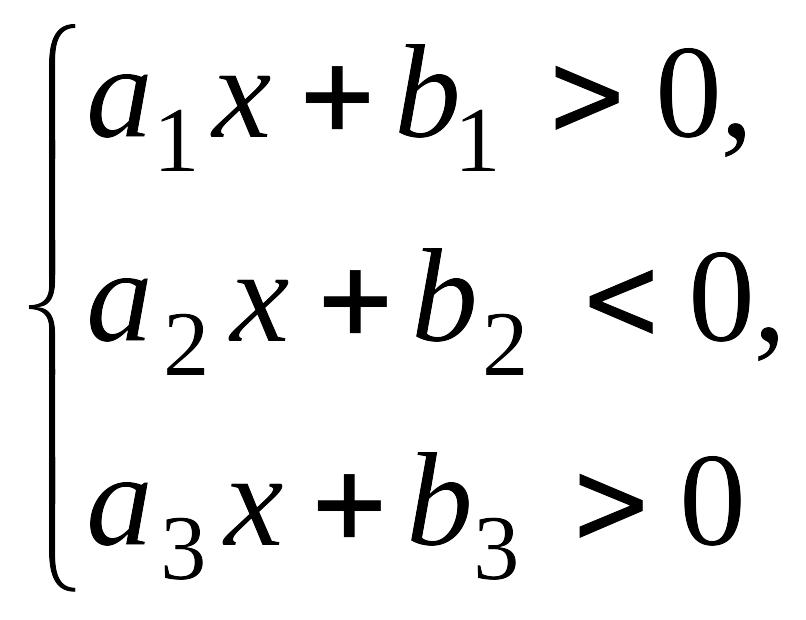
сияқты сызықты теңсіздіктер жүйесін қарастырайық. Ал, мына сызықтық жүйелер жай сызықты жүйелер деп аталады:
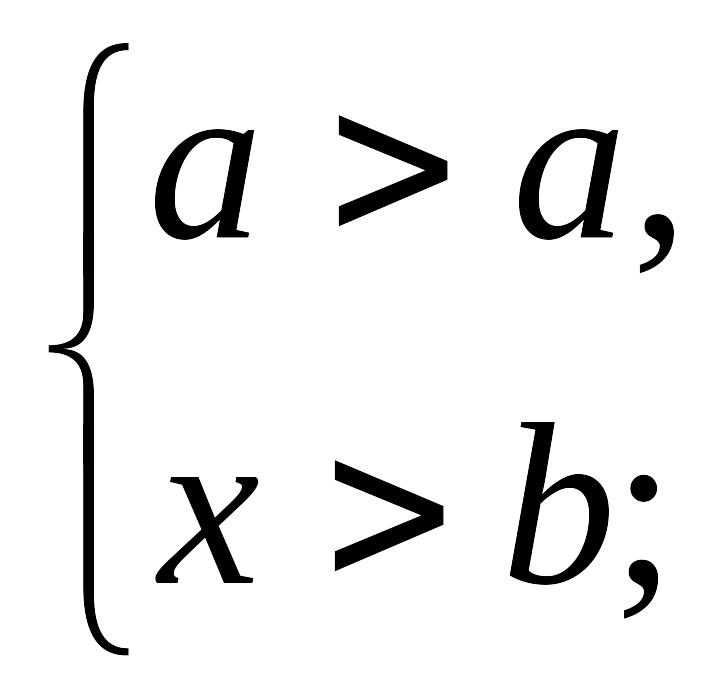
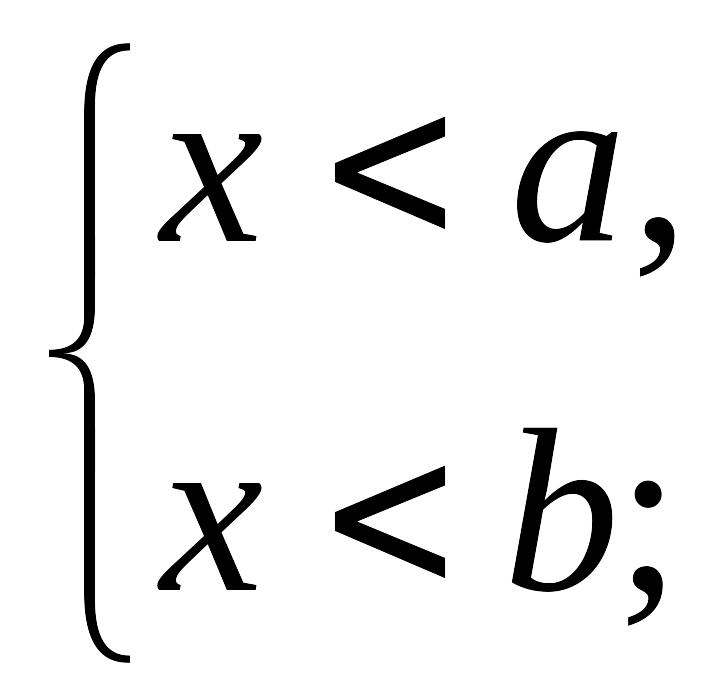(3)
Сызықты теңсіздіктер жүйесі
,
(4)
,
(5)
түріндегі теңсіздіктерді шешуге келтіріледі. Мұндағы –нақты сандар. (4) пен (5) теңсіздіктердің біріншілері және екіншілері өзара мәндес. (4) теңсіздігі
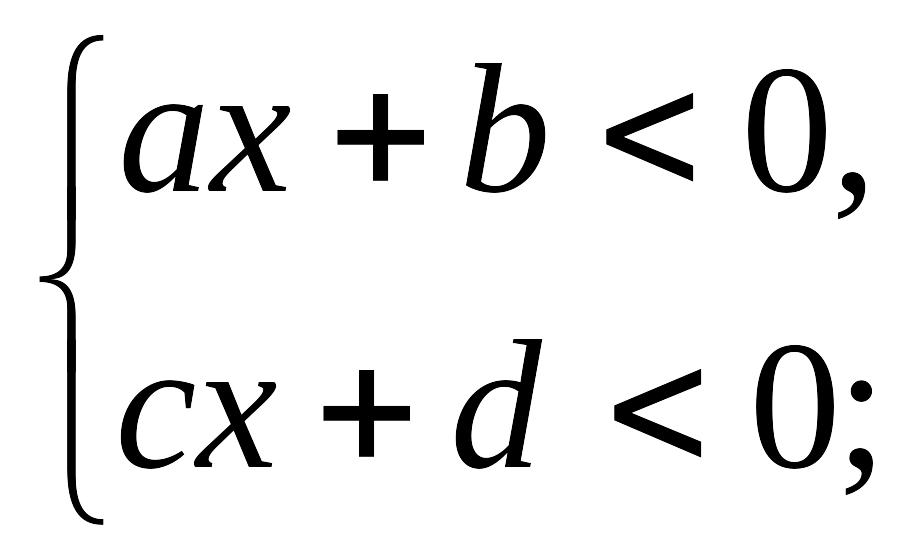(6)
жүйелерінің жиынтығын қанағаттандыратын айнымалы –тің мәндерінде ғана дұрыс болады, яғни (6) теңсіздіктер жүйесінің жиынтығын екі оң көбейткіштің көбейтіндісі не екі теріс көбейткіштің көбейтіндісі оң болғанда ғана қанағаттандырады. (4) теңсіздіктері
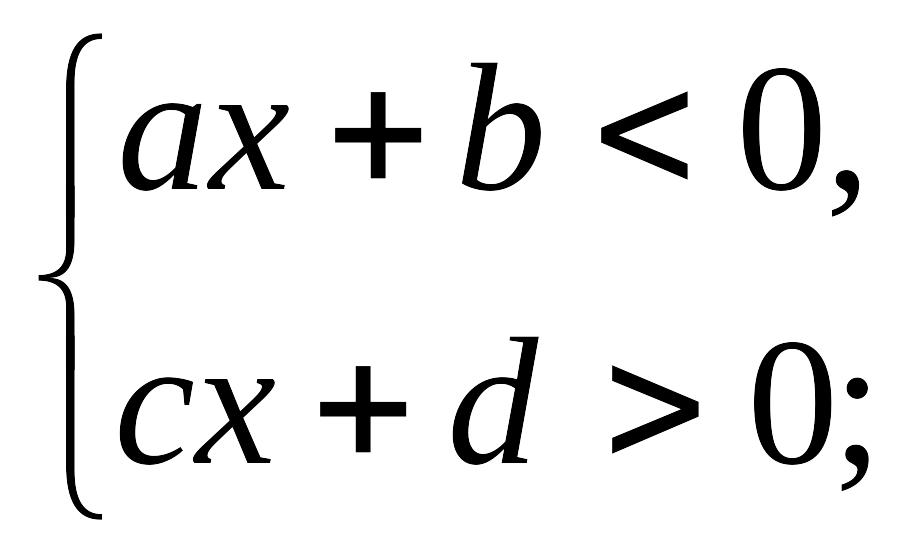(7)
теңсіздіктер жүйесінің жиынтығын қанағаттандыратын –тің мәндерінде ғана дұрыс болады, өйткені таңбалары әр түрлі көбейткіштердің көбейтіндісі ғана теріс болады.
Бөлшек оң таңбалы болуы үшін оның алымы мен бөлімі бірдей таңбалы болуы тиіс, сондықтан (5) теңсіздігі ең болмағанда (6) теңсіздіктердің бірін қанағаттандыратын –тің мәндерінде ғана дұрыс болады.
Бөлшектің алымы мен бөлімі әр түрлі таңбалы болғанда ғана тек сонда ғана бөлшектің мәні теріс болады. Демек, (5) теңсіздіктерінің бәрі ең болмағанда (7) теңсіздіктер жүйесінің бірін қанағаттандыратын айнымалының мәндерінде ғана дұрыс болады. Теңсіздіктерді жалпы алғанда интервалдар әдісімен шешеді.
6. Айнымалысы модулге тәуелді теңсіздіктер
болғанда
(1) теңсіздігі
(2) теңсіздігімен мәндес, ал
болса, теңсіздіктің шешімі жоқ. (2)
теңсіздік
және
теңсіздіктерімен мәндес.
болғанда
(3) теңсіздігі
(4) теңсіздігімен мәндес. Егер
болса, онда (3)–тің шешімі жоқ.
болғанда теңсіздігінің шешімі
аралықтарының бірігуі болады. Ал,
болғанда
–тің
кез келген мәні теңсіздікті қанағаттандырады,
оның шешімі – барлық нақты сандар жиыны,
яғни
.
(4)
теңсіздік
не
теңсіздіктерінің жиынтығымен мәндес.
болғанда
(5) теңсіздігінің шешімі
және
аралықтарының бірігуі болады. Ал,
болғанда
–тің
кез келген мәні теңсіздікті қанағаттандырады.
Айнымалысы модульге тәуелді теңсіздіктерді шешу барысында , функциялардың анықталу аймақтарын ескеру керек:
1)
теңсіздігі
теңсіздігімен мәндес, мұндағы
2)
болса,
теңсіздігінің шешімі болмайды.
3)
теңсіздігі
және
екі теңсіздіктің жиынтығына мәндес,
мұндағы
4)
теңсіздігі
функциясының анықталу аймағына енетін
–тің
барлық мәндерінде дұрыс болады, мұндағы
5)
теңсіздігі
және
теңсіздіктерімен мәндес (
–функциясындағы
аргумент
тек оң мән қабылдайтын болса).
6)
теңсіздігі
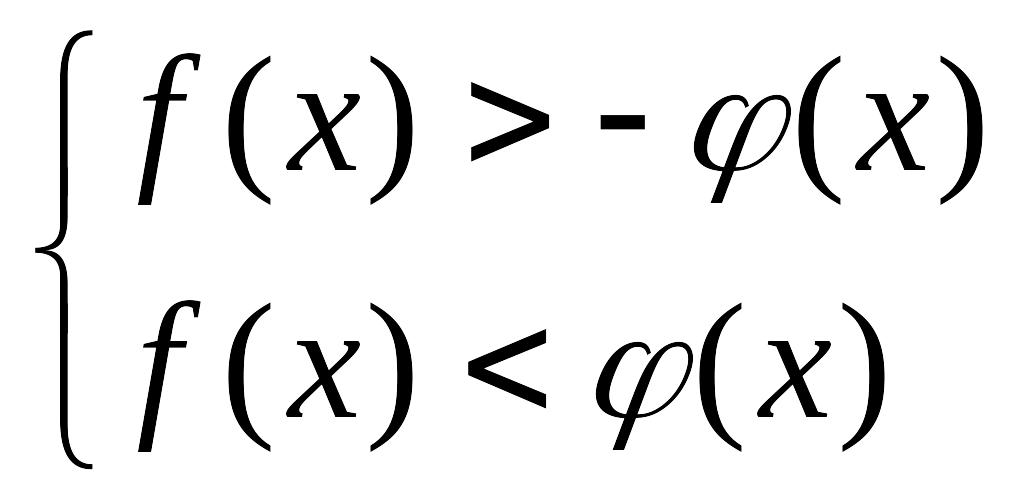теңсіздіктер жүйесімен мәндес.
1-мысал.
теңсіздігін шешу керек.
Шешуі: Бұл (3) теңсіздікке ұқсайды.
Бұл
теңсіздікті
-тің
мәндері қанағаттандырады. Мұны шешсек,
,
яғни
яғни теңсіздіктің шешімі
аралығы.
2-мысал.
теңсіздігін шешу керек.
Шешуі:
Берілген теңсіздік
және
теңсіздіктер жиынтығымен мәндес,
бұлардан
және
Теңсіздіктің шешімі
және
аралықтарының бірігуі болады.
3-мысал.
теңсіздігін шешу керек.
Шешуі:
нүктелері сан осін
аралықтарына бөледі.
болғанда,
болады да берілген теңсіздік
бұдан
Бұл
дегенге қарама-қайшы. Сонымен, бірінші
аралықта теңсіздіктің шешімі жоқ.
да
,
бұдан
бұл
аралығында тиісті емес деген сөз, бұл
екінші аралықта шешімі жоқ дегенді
білдіреді.
Егер
болса, онда
бұдан
- бұл шешім. Олай болса, теңсіздік шешімі
