2.2. Есептер шешу арқылы оқушының ойын дамыту.

. Еліміздің егеменді ел болғалы бері кетелі де ауқымды өзгерістер жүруде.Саяси экономикалық қаржылық тағы да басқа салалардағы секілді білім беру саласы да мұндай өзгерістерден тыс қалған жоқ,себебі мемлекетті нығайту көркейту үшін-өмірге жаңаша көзқарастағы білімді жан жақты дамыған ұрпақ тәрбиелеу қажеттігі туындады.Сондықтан қандай халықтың даму стратегиясын алып қараса онда өскелең жас ұрпақты елін сүйетін отаншыл, саналы тәрбиелі етіп шығару оның басты бағдарламаларының бірі.Қазіргі жас ертеңгі халық тағдырын шешетін азамат.Осыдан білім беру мекемелерінің алдынан күрделі міндеттер тұр. Ол оқушыны саналы ойлайтын ертеңгі күні қоғамды өз орнын табатын жеке тұлғаны тәрбиелеп шығару.

Қазіргі кезеңде саласының алдына қойылған талаптар оқушыларға білімді тереңдетіп беру. Мұны кейінгі жылдары шыққан оқулықтарда көруімізге болады.Мұндай жағдайда оқушының алдында үлкен меселе оқушыны қалайша шаршатпай енжарлыққа салдырмай терең білім беруге болады.Осы тұрғыдан алып қарағанда оқыту үрдісінде ойын әдісін қолдану-бұл проблеманы шешудің бірден бір жолы.

Оқыту үрдісі деңгейін арттыру арқылы,ақыл-ойы жетілген,жан-жақты дамыған,шығармашылықпен еңбек етуге қабілетті,өз тағдырларын өздері шеше алатын, оз бетінше білімін толықтыру және өздігінен кәсіби шеберлігін арттыру мүмкіндігі бар азаматтар даярлау білім саласындағы басты мақсат болып табылады.

Оқушылардың ойлау қабілеттерін дамытуда,қызығушылығын арттыруда,оларды тәрбиелеуде,біліктері мен дағдыларын қалыптастыруда математиканың практикамен байланысын көрсетудің маңызы зор.Математиканы оқытудағы басты мақсаттарға жетуде есеп басты қызметші болып табылады.Әрбір мектеп бітіруші оқушы орта есеппен 15000-дай есеп шығарады екен.Ал солардың көпшілігі жоғары және арнаулы оқу орындарына түсу тестісінде математикадан берілген тапсырмаларды шығара алмай жатады.Бұл әлі де мектеп математикасын оқытуда есеп шығаруға көңіл аз бөлініп отырғанның дәлелі.

Психологиялық,педагогикалық,логикалық,философиялық және әдістемелік зерттеулерге талдау жасап,"есеп", "есептерді шығару" ұғымдарының мән-мағынасын, мазмұнын ашу және негіздеу , оқу есептерінің классификациясын жасау, стандарт және стандарт емес есептерге анықтама беру,оқу есептерінің ойлауды қалыптастырудағы және дамытудағы рөлін анықтау,оқу есептерінің ойлауды қалыптастырудағы және дамытудағы рөлін анықтау,оқу есептерінің міндеттерін айқындау арқылы оқушыларды есептерді стандарт емес тәсілдермен шығаруға баулу олардың білім жүйесін толық игеруіне,ойлау қабілеттері мен ізденушілік әрекеттерінің дамуына елеулі әсерін тигізеді.

Мектепте оқушыларды есептерді стандарт емес тәсілдермен шығаруға баулуға көңіл аз бөлінеді,әсіресе туынды,вектор және интегралды пайдалану тәсілдеріне,сондай-ақ оқушыларды есептерді стандарт емес тәсілдермен шығаруға баулуда көптеген кемшіліктер орын алған (туынды, вектор және интеграл ұғымдарының қалыптасуы мен даму болашағына терең үңілмеу, бұл ұғымдардың қолдануға қажетті тұстарын таба алмау,туынды,вектор және интегралды пайдалану тәсілдері мен стандарт тәсілдер арасындағы әр түрлі байланыстар ман қатынастарға жете көңіл бөлмеу,оқушыларды есептерді туынды, вектор және интегралды пайдаланып шығару тәсілдеріне баулуға арналған есептер жүйесінің рөлін бағаламау және т.б.)

Оқушыларды есептерді стандарт емес шығаруға баулудың жоғары деңгейде болуы үшін арнайы дайындаған есептер жүйесін (туынды,вектор және интегралды пайдаланып шығаруға берілген есептер)қолдану тиімді.

Есептер жүйесін оқу үрдісінде қолданғанда оқушылардың психикалық ерекшеліктері,жекелеген өзгешеліктері және есептерді стандарт емес тәсілдермен шыгаруды игеру қабілеттері ескерілуі тиіс.

Арнайы құрастылған есептерді оқыту мазмұнына жүйелі енгізу бағдарламадағы материалдарды терең оқып үйренуге, оқушылардың оқу үлгерімінің жоғарлауына қолайлв жағдай туғызады.

Ең бастысы арнайы құрастырылған стандарт емес есептер жүйесін оқыту үрдісінің әр түрлі кезеңдерінде үзіліссіз пайдаланудың және Х-Х1 сынып оқушыларын аталған есептер жүйесін туынды,вектор және интегралды пайдаланып шығару тәсілдеріне баулудың сондай-ақ жоғары сынып оқушыларын "Математика в школе" , "Квант", "Алгорифм"журналдарының арнайы ажыратылған "Есептер" бөліміндегі стандарт емес есептерді шығаруға үзіліссіз баулудың маңызы орсан зор деп білеміз.

Қорыта келгенде стандарт емес есептер ғана оқушылардың математикалық ойлауын қалыптастырудың және дамытудың математикалық ойлауын қалыптастырудың және дамытудың математикалық мәдениетін арттырудың,оларды дарындылыққа тәрбиелеудің басты құралы болып табылады, сондай-ақ оқушыларды олардың алдағы іс-тәжірбиелерінде күнделікті тіршіліктегі практикадағы, ғылым мен техникадағы алуан түрлі қиындығы жоғары есептерді шығара білуге дайындайды және тәрбиелейді

1) Есеп шығару кезіндегі ойша орындау мен қабылдау, еске түсіру.

Математикалық есептерді шығару кезінде көптеген ойша орындалатын дағдылар қажет болады.

Есептің берілгендеріне талдау жасау, ізделінді мен берілгендерді, бұрын өтілген есептермен салыстыру берілген жағдайдағы қасиеттерді анықтау, қарапайым модельдерді құрастыру, ойша экспериментті іске асыру, синтездеу, есеп шығаруға қажетті информацияны таңдау, оны бір жүйеге келтіру, бұл информацияны қысқаша текст, символика, график түрінде тұжырымдап есеп шығаруға қолдану. Есеп шешімін жалпылау, берілгендер арасындағы ерекше жағдайды зерттеу. Есеп шығару кезінде осы заманғы психологияның жетістіктерін пайдалану. Психологтары есептерді бір сыныптың әр оқушылары әр түрлі формада түсінеді. Математикаға қабілетті оқушы есептердің дербес элементтерін, бір тұтас комплекстегі өзара байланысты элементтерді, комплекстегі әрбір элементтердің ролін түсінеді. Орташа оқушы есептің дербес элементтерін ғана түсіне алады. Сондықтан есептерді шешуді үйреткен кезде есеп элементтердің арасындағы қатысты арнайы талдау керек. Бұл есептер шартын талдауға қажетті тәсілдерді таңдап алуға мүмкіндік береді. Есеп шығару кезінде көбінесе бұрын өтілгендерді еске түсіруге тура келеді. Қабілетті оқушы ең қажетті информацияны «жалпыланған, структурасы қабаттасқан» информацияны есінде қалдырады. Есте сақталған информация мида асып төгіледі, есте қалғандары пайдалануға оңай, оңай есте қалады. Есептер шешу кезіндегі жалпылау тек ойды дамытып қана қоймай, еске сақтауды да және «жалпыланған ассоциацияны» қалыптастырады. Есеп шығару кезінде осылардың бәрін ескеру керек.

2) Ойлауды оқыту.

Математикалық есептер мен жаттығулардың тиімділігі көбінесе оқушылардың есептер шешу кезіндегі творчестволық белсенділігінің дәрежесіне тікелей байланысты. Есеп оқушылардың сабақтағы ойлау қызметін белсенді қалыпқа келтіреді. Есептер оқушылардың ойын оятып, оны жұмыс істеуге ойлануға мәжбүр етеді, сол арқылы дамып жетіледі.

Оқушылардың ойын дамытқанда – салу, түрлендіру, тұжырымдарды еске сақтау арқылы дәл ойлауға, талқылай білуге, фактілерді қарастыра білуді, жалпы және әр түрлі ой қорытындысын жасауды үйренеді.

Математика мұғалімінен жалпы іргелі және арнайы математикалық білім ғана емес, педагогтік қызметке шығармашылықпен қарау, іскерлік белсенділік көрсету арқылы өз білімін үздіксіз жетілдіру қабілеті де талап етіледі. Дәл осындай қасиеті бар мұғалім қоғамның жедел өзгерістеріне тиімді түрде бейімделе алады.

Сондықтан, орта мектептің математика курсының ең басты міндеті есеп шығарудың әдістемелік жақтарына даярлауға тіреледі.

Математикалық теориялық негізін есеп түрінде меңгеру болашақ мұғалімдердің ойын белсендіреді, икемділік, тереңдік, жинақылық, жүйелілік, шапшаңдық және т.б. шығармашылық тәрізді математика мұғаліміне қажетті қасиеттерді қалыптастырады.

Осыған орай, студенттерді шығармашылық қабілетке шыңдау мәселесі туындайды.

Педагогикалық оқу орнындағы математика курсындағы математикалық есеп студенттің ұғымдарды, теорияны, және математика әдістерін меңгерудің тиімді, қажетті құралы. Студенттердің ойлау қабілеттерін дамытуда, оларды тәрбиелеуде біліктіліктері мен дағдыларының қалыптасуында, математиканың практикамен байланысын көрсетуде есептің маңызы зор. Есеп шығару – ой жұмысы. Ой жұмысы арқылы студенттің дербес ойлануға, қорытынды шығарып, математикалық ақиқатты көре білуге, дәлдікке үйренеді. Сондай-ақ, есепті бірнеше әдіспен шығару да ізденушілік қасиетін, шығармашылықпен жұмыс істеу қабілеттілігінің дамуына көп көмектеседі. Енді жоғары дәрежелі теңдеулерді шешу әдістерін топқа бөліп қарастырайық.

№ 8-9 лекция.

Тақырыбы «Теңдеулер, теңсіздіктер және олардың жүйелерін шешудің жалпы тәсілдеріне үйрету».

1. Рационал және бөлшек-рационал теңдеулер, теңсіздіктер және олардың жүйелері.

2. Иррационал теңдеулер, теңсіздіктер және олардың жүйелері.

3. Көрсеткіштік және логарифмдік теңдеулер, теңсіздіктер және олардың жүйелері.

4. Тригонометриялық теңдеулер, теңсіздіктер және олардың жүйелері.

Квадрат теңдеулер

(1) түріндегі теңдеуді квадрат теңдеу деп атайды. Мұндағы -ай- нымалы -нақты сандар, -квадрат теңдеудің бас коэффициенті, -екінші коэффициенті, -бос мүшесі деп аталады.

мен коэффициенттерінің ең болмағанда бірі нөлге тең болса, онда теңдеуді толымсызквадрат теңдеу деп атайды.

Егер онда

Егер , ( мен -ның таңбасы бірдей емес). Егер онда (1) теңдеуді түріне келеді, мұның түбірлері .

өрнегін (1) теңдеудің дискреминанты деп атайды.

Егер болса, онда (1) теңдеудің (2) түбірі бар.

Егер болса, , өзара тең екі түбірі бар. Мұндай жағдайда теңдеудің еселі түбірі бар деп есептейді. болса, теңдеудің нақты түбірі жоқ.

1-теорема: квадрат теңдеуінің түбірлерінің қосынды- сы , ал түбірлердің көбейтіндісі ға тең.

, (3) Осы теореманы Виет теоремасы деп атайды. Бұл теоремаға кері теорема да дұрыс болады.

2-теорема: Егер -сандарының қосындысы -ға, ал көбейтіндісі болса, онда ол сандар теңдеуінің түбірлері болып табылады.

Егер теңдеуіндегі болса, онда 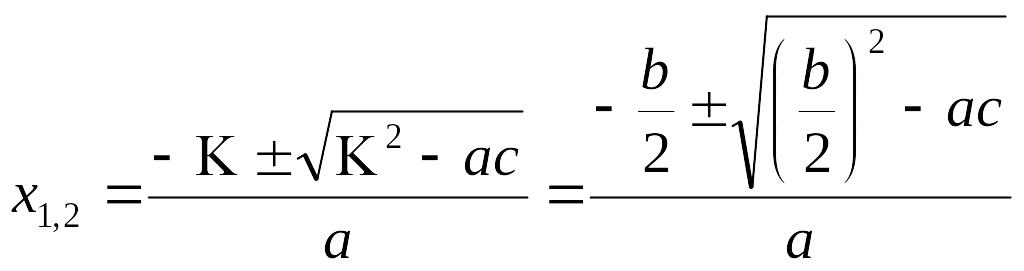(4). Егер теңдеуінің әр мүше- сін -ға бөлсек, онда (5) келтірілген теңдеу деп аталатын теңдеу шығады, мұндағы , . Оның түбірлері (6) формуласымен табылады. (3) теңдеуді

, (7) түрінде жазу қолайлы.

Егер (1) квадрат теңдеуінің түбірлері болса, онда оны (8) түрінде жазады, егер болса, онда (8) теңдеу

(9) түрінде жазылады.

(10) түріндегі теңдеуді биквадрат теңдеу деп атайды. Оны шешу үшін деп белгілеп, квадрат теңдеуге келтіреді.

1-мысал: теңдеуін шешейік.

Шешуі: , .

2-мысал: квадрат үшмүшені көбейткіштерге жіктеңдер.

Шешуі: . .

Сонымен,

Иррационал теңдеулер

Айнымалысы түбір астында болатын теңдеулерді иррационал теңдеулер деп аталады.

Мұндай теңдеулерді шешкенде түбір дәрежесі қанша болса, сонша дәреже шы -ғарып, түбірді «бөлектеу» айнымалы ендіру, түйіндесіне көбейту, теңдеулердің аралас жүйесіне келтіру т.б. әдістермен шешеді.

Мұндай теңдеулерді шешкенде қосылғыштардың әрқайсысы оң болуы тиіс.Түр- лендіргеннен соң табылған түбірді міндетті түрде тексеру керек немесе алдын-ала анықталу аймағын табу керек.

(1) болса, ол (2).

1-мысал: теңдеуін щещу керек.

Шешуі: , . Бұл жағдайда

Теңдеудің екі жағын квадраттасақ, ,

, .

-ғана анықталу аймағына тиісті. Теңдеудің түбірі .

2-мысал: теңдеуін шешу керек.

Шешуі: Түбірді бөектеу әдісі бойынша , енді теңдеудің екі жағын квадраттасақ, , , , , .

Анықталу аймағы . Ендеше теңдеудің түбірі .

2-мысалда берілген есепті жаңа айнымал ендіру әдісімен де шешуге болады, ол үшін деп жаңа айнымалы ендіреміз. Теңдеулердің оң және сол жақтарын көбейтсек, бұлардан

.

, .

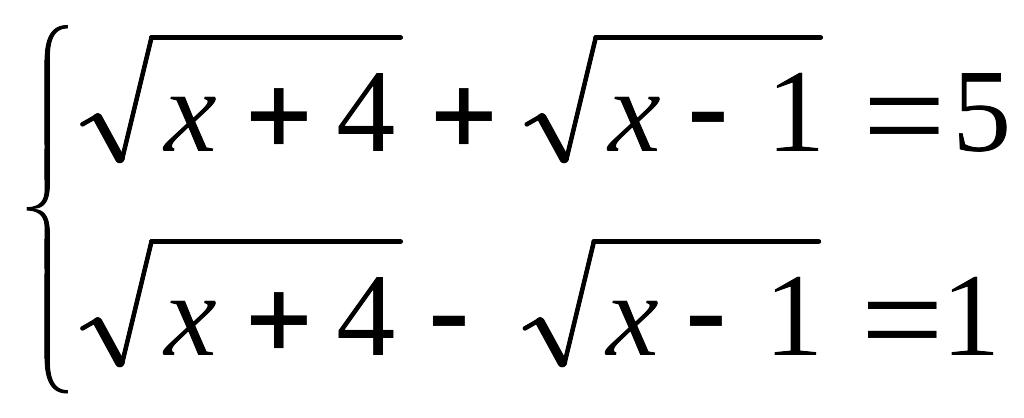
Көрсеткіштік теңдеулер

Айнымалысы дәреже көрсеткішінде болатын теңдеуді көрсеткіштік теңдеу деп атайды.

түріндегі теңдеуді көрсеткіштік теңдеу дейді. Мұндағы -нақты сандар, .

функциялары -айнымалыға тәуелді функциялар белгілі бір -жиынын- да анықталады. болғандықтан, көрсеткіштік теңдеуді түрін –де жазуға болады, мұндағы .

Теорема: (1) көрсеткіштік теңдеуі (2) теңдеуімен мәндес. Дербес жағдайда , теңдеуі берілсе,

Одан -түріне келуі не болуы мүмкін. Бұдан басқа жағдайлрда теңдеу -дің екі жағын негізде логарифм деп шешеміз.

Егер көрсеткіштік теңдеу , түрінде берілсе, онда болға- ны. Кейде көрсеткіштік теңдеу түрінде берілуі де мүмкін.

1-мысал: теңдеуін шешу керек.

Шешуі: Теңдеудің сол жағынан -ін жақша сыртына шығарсақ,

2-мысал: теңдеуін шешу керек.

Шешуі: онда бұдан , .

3-мысал: 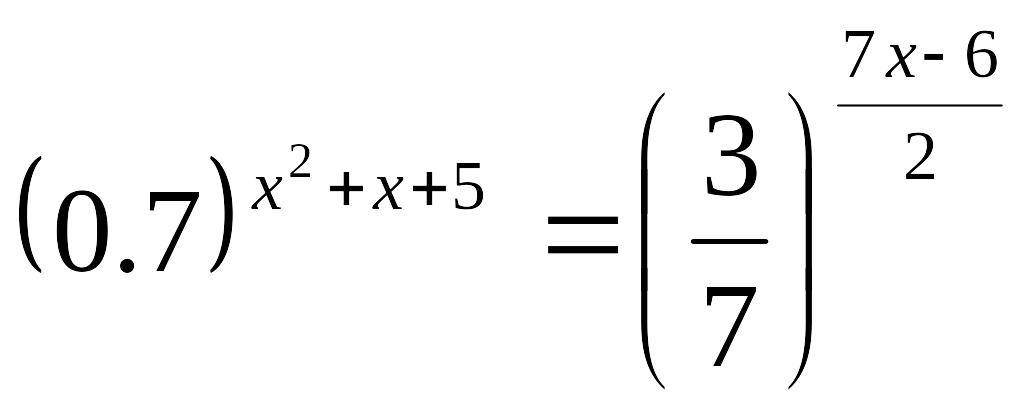теңдеуінен түбірлердің көбейтіндісін табыңдар.

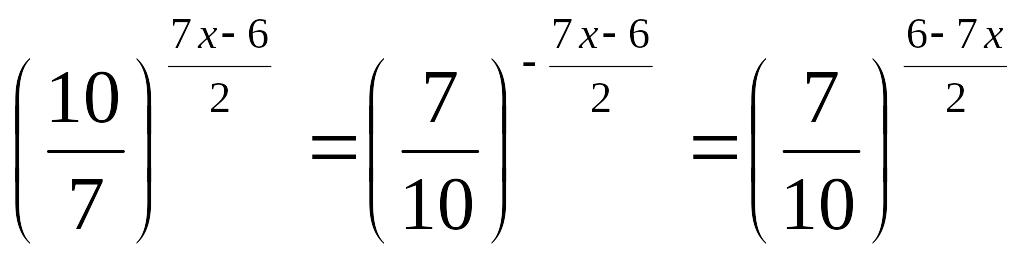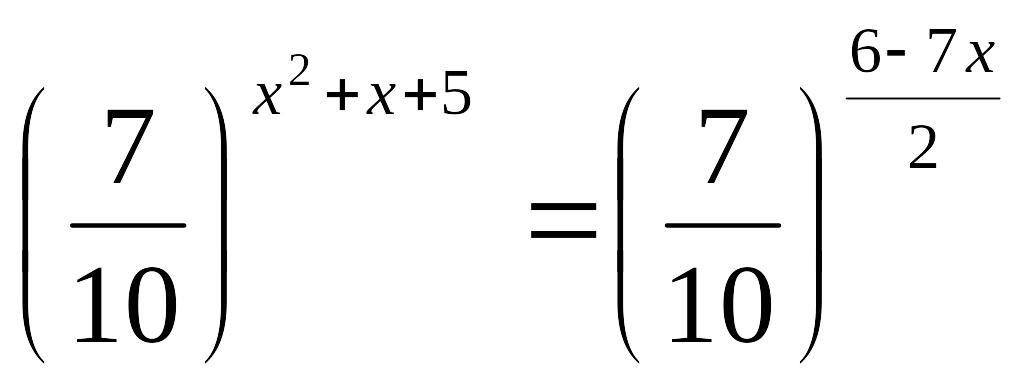Шешуі: , олай болса, берілген теңдеу түрінде жазылады, бұдан аталған теореманы ескеріп, мұны шешсек, .Бұлардың көбейтінді- сі

4-мысал: теңдеуін шешу керек.

Шешуі: Теңдеудің екі жағын -ке бөлеміз, сонда яғни

, десек, онда теңдеу түрінде болады, бұдан

.

5-мысал: теңдеуін шешу керек.

Шешуі: Алдымен периодты бөлшекті жай бөлшекке айналдыру керек.

, .

Логарифмдік теңдеулер

Айнымалысы логарифмге тәуелді теңдеулерді логарифмдік теңдеулер деп атайды: мұндағы

Егер негіздері бірдей болса, онда логарифмдік теңдеу (1).

Түрінде жазылады. Мұнда да (2)

(1) теңдеуден оның салдары ретінде (3) теңдеуін жазуға болады.

(2) шарт орындалса, онда (1) теңдеуден (3) ке көшкенде түбір жоғалмайды.(1) тең- деу , (4) деген (4) жүйеге мәндес.

Дербес жағдайда болса, онда (1) теңдеу (5)

түрінде болады. Бұл соңғы теңдеу , деген аралас жүйеге мәндес. Логарифмдік теңдеулерді шешкенде келесі түрлендірулер қолданылады:

потенцирлеу (логарифмнен арылу), негізгі логарифмдік теңпе-теңдікті қолдану, логарифмдердің бір негізінен басқа негізге көшу, логарифмнің қасиеттерін қолда- ну, теңдіктің екі жағын белгілі бір негізде логарифмдеу т.с.с.

Жоғарыда айтылғандай (2) шарттарды ескере отырып, (1) теңдеуден онымен мәндес (3) теңдеуге көшуді потенцирлеу деп атайды. (2) шарттарын ескергендік- тен бұл арада түбір жоғалу болмайды, бірақ бөгде түбір пайда болуы мүмкін.

1-мысал: теңдеуін шешу керек.

Шешуі: Берілген теңдеудің анықталу аймағы берілген

теңдеуді потенцирлеп мұның түбірлері Анықталу аймағына тиісті тек

Негізгі логарифмдік тепе-теңдікті қолдану

Бұл түрлендірудің мәні (6) теңдеуінен шығады.

2-мысал: теңдеуін шешіңдер.

Шешуі: болғанда теңдеу анықталады. Логарифм жөніндегі негізгі тепе-теңдікті қолданып, берілген теңдеуден болуы керек, сондықтан теңдеудің түбірі .

Логарифмнің жаңа негізге өту формуласы (7). Мұндағы

3-мысал: теңдеуін шешу керек. Анықталу аймағы

Берілген теңдеуді 2 негізде басқаша жазайық.

десек, 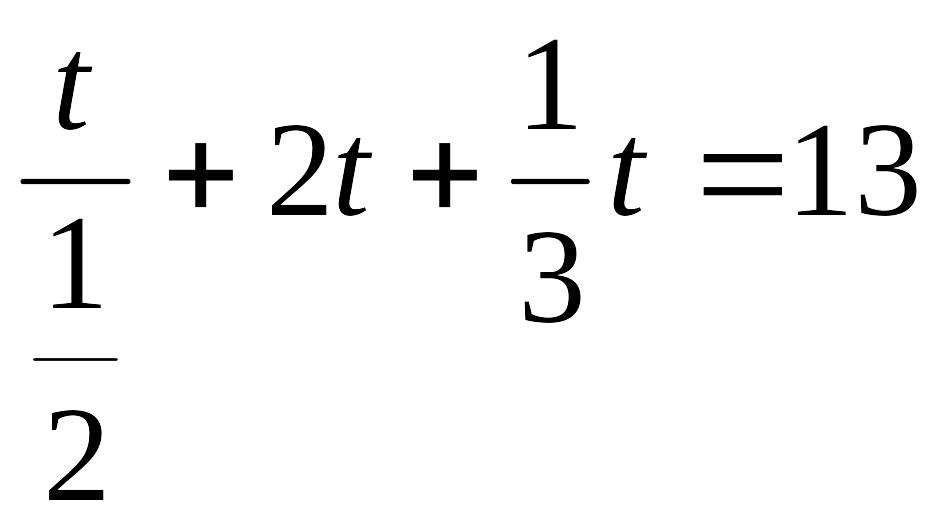немесе

,

Есептер шешкенде логарифмнің қасиеттерін қолдану

4-мысал: теңдеуін шешіңдер.

Шешуі: Логарифмнің қасиеті бойынша

.

Анықталу аймағынан Олай болса түбірі ғана анықталу аймағында жатады.

5-мысал: теңдеуін шешу керек.

Шешуі: Теңдеу болғанда анықталады. Берілген теңдеудегі негізі ре –тінде логарифмдесек, десек,

Мұны шешсек, Бұдан теңдеуге түбір.

Бұл арада болғандықтан теңдеудің түбірі

№ 10 лекция

Алгебралық теңдеулермен теңсіздік жүйесіне келтірілетін есептер

1-мысал: Екі таңбалы санның цифрларының қосындысы .Егер ізделінді саннан

-ды азайтса, онда одан шығатын айырмадағы цифрлар ізделінді сандағы цифр -лардың орындары ауысып жазылған сан шығады. Ізделінді санды табыңдар.

Шешуі: Ізделінді екі таңбалы санның ондық цифрын , бірлігін әрпімен белгі- лесек, онда ізделінді сан ал -цифрларының орындары ауысқан сан. Есеп шартынан немесе

Соңғы жүйені шешсек, ізделінді сан

2-мысал: Кітапханада ағылшын, француз, неміс тіліндегі кітаптар бар. Ағылшын тіліндегі кітаптар барлық шет тіліндегі кітаптардың -і, ал француз тіліндегісі ағылшын тіліндегі кітаптардың -і. Қалған кітап неміс тіліндегі кітаптар. Кітапханада шет тілінде барлығы қанша кітап бар?

Шешуі: Барлық шет тіліндегі кітаптар санын десек, -ағылшын тілінде, -француз тілінде, -неміс тіліндегі кітаптар.

Демек, осы теңдіктен

не

, кітап.

3-мысал: Завод қаңтарда өзінің айлық тапсырмасын -ке орындады, ал ақпан- да қаңтардағыдан көп орындады. Завод екі айлық жоспарын неше процентке артық орындады?

Шешуі: Заводтың бір айда орындайтын тапсырмасының мөлшері болсын. Бұл жағдайда қаңтарда ақпанда екі айда жоспар- да екі айда орындағаны .Бұл неше процентті құрайды?

Демек, завод екі айлық жоспарын -ке артық орындады.

4-мысал: Саяхатшы екі қаланың арасын күнде жүріп өтті. Бірінші күні барлық жолдың бөлігін және екінші күні барлық жолдың -і және , үшінші күні барлық жолдың бөлігін және қалған жолды жүрді. Екі қаланың ара- сы қанша километр?

Шешуі: Екі қаланың арасы болсын. Онда есеп шарты бойынша бірінші күні екінші күні үшінші күні жүрді. Үш күнде барлық

жолды жүргендіктен

5-мысал: Мыс пен мырыштың қоспасында мыс бар. -тік мысы бар жаңа қоспа алу үшін осы қоспаға қанша таза мыс қосу керек? қоспада мыс мөлшері яғни мыс бар. Қоспаға қосылатын мыс мөлшерін десек, жаңа қоспадағы мыс мөлшері осы қоспадағы мыс, Жаңа қоспадағы мыс болуы керек еді, ендеше бұдан

6-мысал: Бір су құбырында екіншісінде су бар. Егер шүмектерді аш- ып қойғаннан кейін құбырлар неше сағаттан соң толады? Егер екінші құбырға са -ғат сайын су артық құйылатын болса, онда неше сағаттан соң екі құбырдағы су мөлшері бірдей болады?

Шешуі: Бірінші құбырдың толтыру жылдамдығы ,екіншісінікі .

Егер шүмектер сағат ашық тұрса, онда бірінші бассейінде , екінші –сінде су болады. Бұл су мөлшері бірдей. Демек,

бұдан сағат өткенде екі құбырдағы су мөлшері бірдей болады.

7-мысал: Электропоезд қаласынан шығып өзінің жүруге тиісті жолының -ін

яғни жүргеннен соң жолда жарты сағат кідіріп қалды. Кешікпеу үшін жүргі- зуші жылдамдығын -қа арттырып, қаласына өз уағында келді. Поездің бастапқы жылдамдығын табу керек.

Шешуі: Поездің бастапқы жылдамдығы , онда соңғы жылдамдық . Есеп шартына сүйеніп уақыт бойынша теңдеу құрсақ,

бұдан бұдан

8-мысал: Бір бригада егістікті күнде, екіншісі осы жұмысты аталған уақыттың -де орындай алады. Бірінші бригада жеке өзі күн егісті жинаған соң оған екінші бригада келіп қосылды. Екеуі бірлесіп жұмысты аяқтады. Екі бригада жұ -мысты қанша күн бірге істеді?

Шешуі: Бүкіл жұмысты бүтін есептесек, онда бірінші бригаданың жұмыс өнім –ділігі екінші бригада жұмысты жеке орындауына күн қажет, оның жұ -мыс өнімділігі . Бірінші бригада күнде жұмыстың бөлігін орындайды. Қал- ған -күнде екі бригада жұмыстың бөлігін орындайды. Ендеше есеп шар- ты бойынша теңдеуін жаза аламыз. Осы теңдеуді шешсек, . Демек, екі бригада бірлесіп күн жұмыс істейді.

9-мысал: Магазинге сату үшін физика және математика оқулықтары түсті. Мате –матика оқулығының -і физика оқулығының сатылғаннан соң барлығы оқулық сатылды.Және физика оқулығына қарағанда математика есе көп қал- ғаны белгілі болды. Магазинге әрқайсы оқулықтан қанша түскен?

Шешуі: Магазинге математика оқулығы, физика оқулығы сату үшін қойылды дейік. Бірінші рет оқулық сатылды. Мұның -і математика, -і физика болғандықтан математикадан физикадан кітап сатылған. Олай болса, теңдігін жазуға болады. Есеп шарты бойынша Бұлардан жүйе құрсақ, Демек, математика оқулығы,

оқулығы сатуға шығарылған.

10-мысал: Спорт мектебінің үш секциясында спортшы бар. Мұзда сырғанаушы спортшылар саны шаңғы тебушілердің бөлігін құрайды.Ал,хоккейшілер алғаш- қы екі секциядағы спортшылардың -ін құрайды.Әр секцияда қанша спортшы-

дан бар?

Шешуі: -мұзда сырғанушылар, -шаңғы тебушілер, -хоккейшілер саны болсын.

Есеп шарты бойынша хоккейшілер алғашқы екі секцияның үштен біріндей

яғни Соңғы жүйені шешсек,

Демек,

11-мысал: Жаяу мен велосипедші арақашықтығы . мен орындарынан кез- десу үшін бір мезгілде жолға шықты. Жолға шыққаннан кейін сағат өткенде олар кездесті. Олар өз бағыттарымен одан әрі жүрді.Жаяудың -ға келуінен вело- сипедші сағат бұрын -ға келді. Егер олар жолда тұрақты жылдамдықпен қозғалса, онда велосипедші мен жаяудың жылдамдықтарын табыңдар.

Шешуі: -жаяудың, -велосипедшінің жылдамдығы болсын. са -ғат өткенде кездесетіндіктен Жаяу жолда сағат, вело-

сипедші сағат болды. Жаяуға қарағанда велосипедшінің уақыты сағат аз. Сондықтан , бұл теңдеудің түбірлері және Жаяу жылдамдықпен жүре алмайды. Жаяу , ал велосипедші

жылдамдықпен жүрген.

12-мысал: Әрқайсысындағы мыс мөлшері әртүрлі екі қоспа бар. Бірінші қоспада- ғы мыстың мыстың мөлшерін процентпен анықтайтын сан екінші қоспадағы мыс мөлшерін процентпен өлшейтін саннан -қа кем. Бұл екі қоспаны қосып қорыт-қанда шыққан қоспадағы мыс мөлшері болды. Егер бірінші қоспада , екін- шісінде мыс болса, онда әр қоспадағы мыстың проценттік мөлшерін анықтаң- дар.

Шешуі: Бірінші қоспада мыс, екіншісінде мыс бар екен дейік. Бірінші қоспаның массасы , екіншісінікі болсын. Бірінші қоспадағы мыстың мөлшері болғандықтан

Дәл осы сияқты екінші қоспада мыс болғандықтан Екі қоспаны қорытқаннан соң масса шығады, бұларда

мыс бар. Жаңа қоспадағы мыстың мөлшері , олай болса, бұдан шығады. екенін ескерсек, Бірінші қоспадағы мыс мөлшері , екіншісінде .

Көрсеткіштік-логарифмдік теңдеулер жүйесі

Мұндай теңдеулерді логарифмдеу, потенцирлеу, айнымалыны ауыстыру т.б.

әдістермен шешуге болады.

1-мысал:

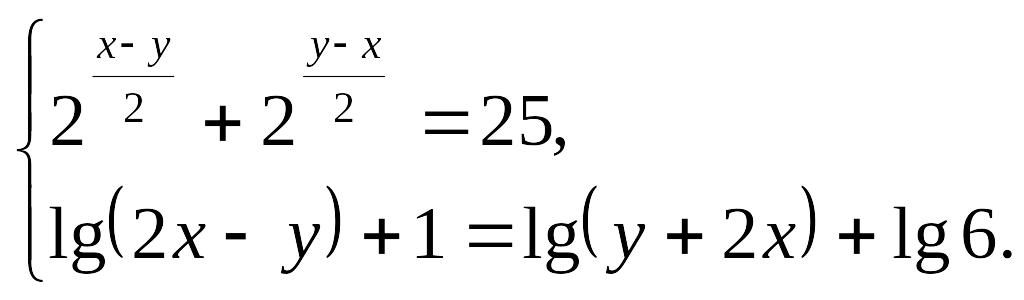
Шешуі: десек, онда және .

Демек, бұлардан (1). Біріншісінен Осы

мәнді жүйенің екінші теңдеуіндегі тің орнына қойсақ, бұдан бұдан потенцир- лесек, онда

теңдеуінен мұны берілген жүйенің екінші теңдеуіне қойсақ,

потенцирле -сек. ,

Бұл соңғы шешім анықталу аймағына енбейді. Жауабы

2- мысал. 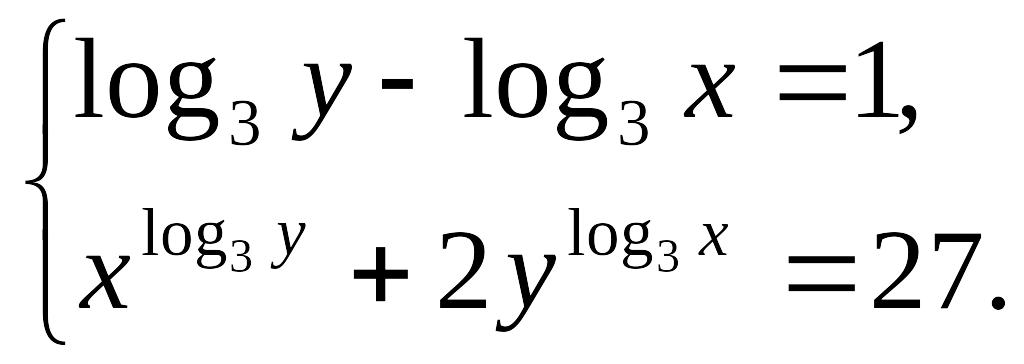теңдеулер жүйесін шешу керек.

Шешуі: Жүйенің екінші теңдеуін логарифмнің қасиетін пайдаланып, бұдан -осы теңдеудің екі жағын 3 негізде логарифмдесек,

Бұл арадан белгілеу ендірсек,

жүйе аламыз.

Бұларға сәйкес айнымалыларына ауыссақ,

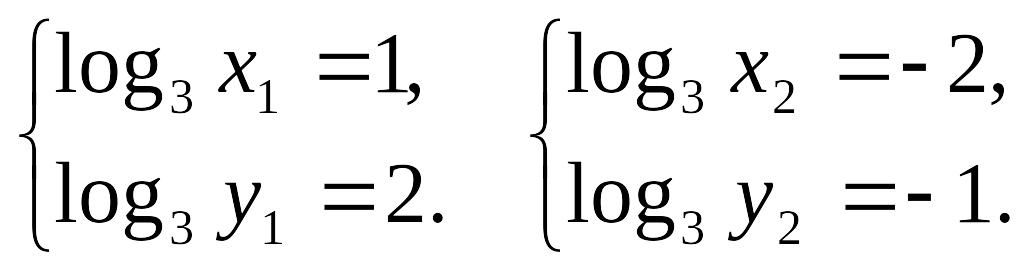бұлардан

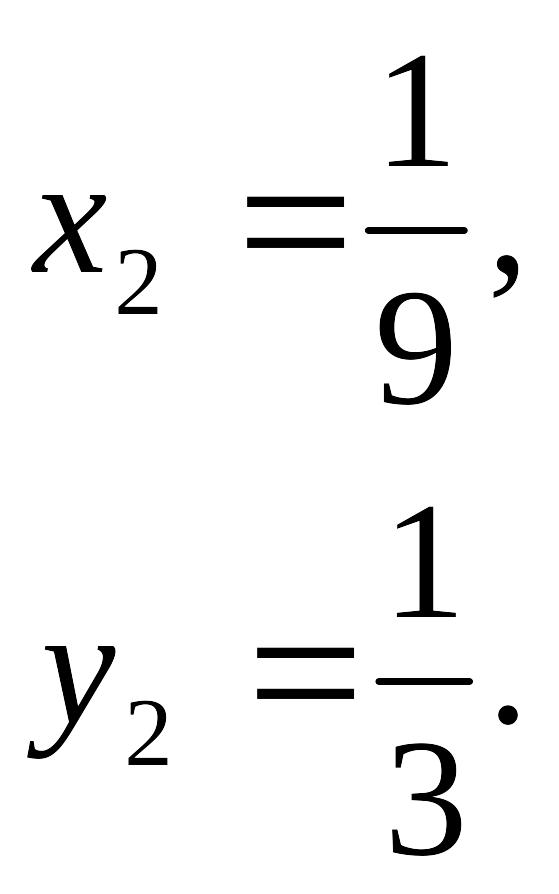Жауабы:

3- мысал. 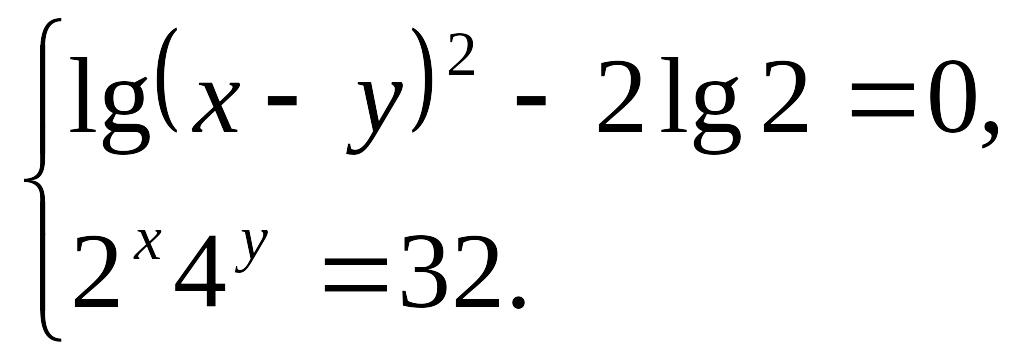теңдеулер жүйесін шешу керек.

Алдымен мәнін жүйенің екінші теңдеуіне қоямыз

Жүйенің екінші теңдеуіне ні қойсақ :

Жауабы :

№ 11-12 лекция

Теңсіздіктер