2. Алға қойған дидактикалық мақсаттарына қарай есептерді топтау.

0. Математиканың теориялық мәселелерін үйренуге дайындық жасау – дидактикалық мақсатын алға қояды. Жаңа теориялық мәселелерді оқушының есінде қалдыру үшін жаңа фактілерді келтіреді. Дидактикалық мақсат ретінде жинақталған теориялық білімді бекіту үшін математикалық есептер шешіледі.

1. Бұл математикалық ұғымды меңгеру, олардың анықтамалары мен білік қалыптастыру теорема, аксиома тұжырымды бекіту, дәлелдеу методын бекіту үшін есептер шешу

Мәселен, рационал көрсеткішті дәреженің қасиетін үйренудің алдында бүтін көрсеткішті дәреженің қасиеттері қолданылған есептер шешіледі.Рационал сандар үшін көбейтудің қосуға қатысты үлестірімділік заңын өтер алдында осы заңды бүтін сандар үшін қолданып жаттығу орындау керек.4-6 сыныптарда жаттығулардан соң мұғалім жаңа сөйлем, анықтама, алгоритм тұжырымдап алатын болуы керек. Оң, теріс сандарды көбейтудің алдында термометрді пайдалану. Санның таңбасы мен модулі, көбейтіндісі оларды сәйкес шамалармен сипаттау арқылы көбейтуді орындаудың заңдылығын табу.

Теориялық мәліметтерді үйрену үшін келесі есептер:

• Екі бұрыштың ортақ төбесі бар. Олар сыбайлас емес және вертикаль бұрыштар ұғымын бекітуге арналған.

• Виет теоремасын бекіту үшін

Х²+рх+35=0 бір түбірі – 7, екінші түбірі мен р коэфициентін тақ деген сияқты жаттығу орындау керек.

0. Үйренген оқу материалын иллюстрациялау. Мысалы, теңбе-тең түрлендіру: мысалы (а+в)²-(а-в)², .

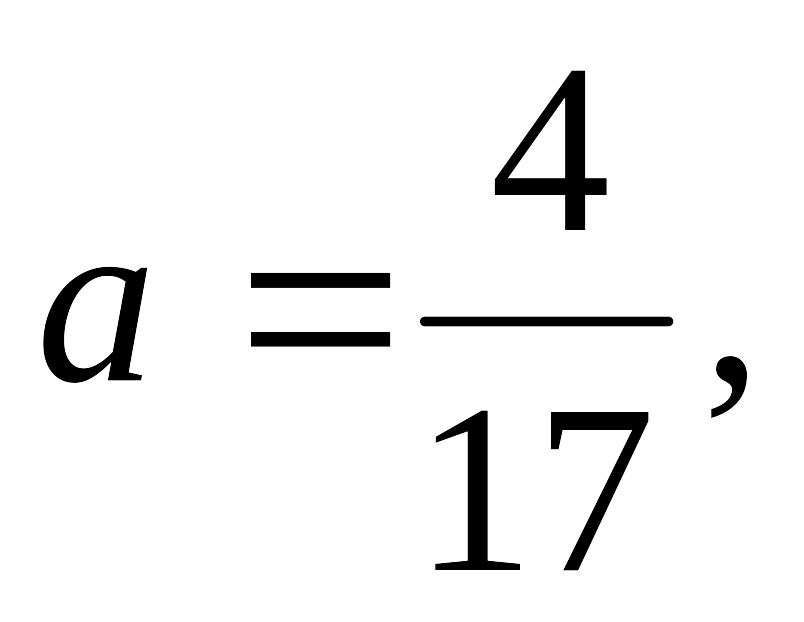
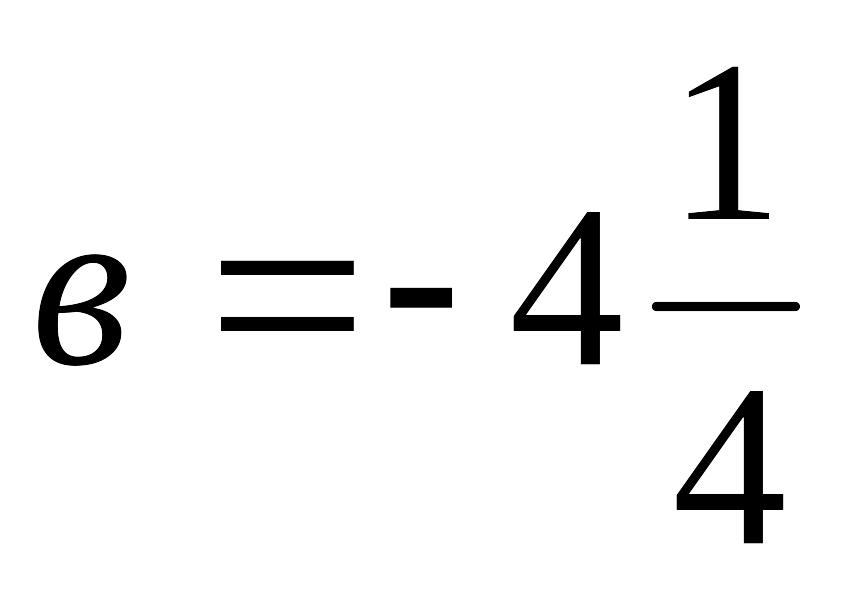Тікелей есептеу өте қиын, ықшамдасақ (а-в)²-(а-в)²=4ав бұдан соң ауызша есептеуге болады.

0. Есептер мен жаттығулар арқылы білік және дағды қалыптастыру.

Білік қалыптастыру – ең алғаш есеп шығара бастағанда жаңа тәсіл, алгоритм мен кейбір сыныптың есебін шешудің әдісін меңгереді. Оқушылар нақты жағдайларға жалпы тәсіл, алгоритм, метод қолданады.

Мысалы: Бөлшек сандарды көбейтуді үйретуде мына мысалды дәл етіп жазу

Көбейту алгоритмі мысалдар арқылы қалыптасады. Осындай 3-4 есеп шығарған соң жазуын жазбаса да болады. Не

Математикалық дағды қалыптастыру жеке есеп емес, бүкіл есептер жүйесінде дағды қалып ойланбай, қай формула деп таңдап алмай автоматты түрде көптеген тәсілдер мен әдістерді еркін қолдана білуді дағды дейміз.

Дұрыс ойластырылған дағды жаттығулар жүйесінде және есептер шешуде қалыптасады. Мұндай жүйе жаттығулардың тізбектілігі оқушылардың мүмкіндігі мен жас ерекшеліктеріне қарай реттеліп келуі керек.

Мысалы: Қысқаша көбейту формуласының жәрдемімен көбейткіштерге жіктегенде ортақ көбейткішті жақша сыртына шығарғаннан кейін көбейткіштерге жікте

72а²в⁴с-2в²с; 2) 0,2mn³+0,2mn-0,4mn².

және теңдеуді шешіңдер.

Интегралдарды үйренгенде оларды есептеу системасында басқа амалдар ендіру пайдалы.

Теңсіздікті шеш

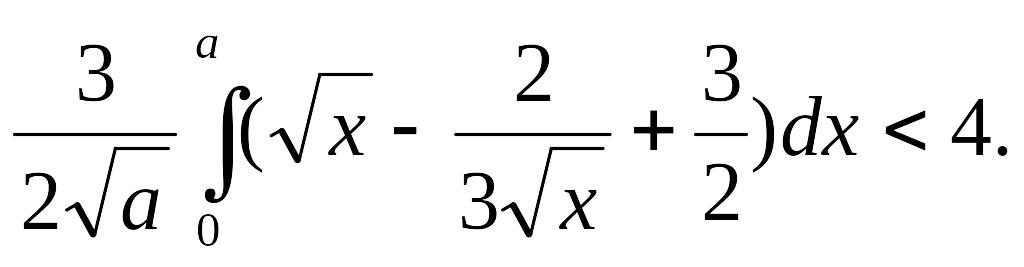
дидактикалық мақсатты іске асыруда бұрын өтілгенерді қайталау.

Есептер шешу кезінде бұрын алған білім, білік дағдыларын қолданады. Математикада өзінен-өзі қайталау болып жатады.

3.Математика есептерін шешуді ұйымдастыру.

Оқушыларға есеп шешудің әр алуан әдістерін үйрету мұғалімнің маңызды да жауапты міндеттерінің бірі. Бұл мәселе әр түрлі тәсілдерімен жүзеге асырылады .Есеп шешуге үйрету ісін ұйымдастыру класта,үйде оқушылардың жеке ерекшеліктеріне қарай дербес тапсырмалар беру, сондай-ақ ұжым болып орындау арқылы жүргізіледі. Енді есеп шешуге үйретудің төмендегідей түрлері бар:

1.Есепті жаппай шешу. Есепті жаппай шешу деп бір есепті барлық оқушылардың бір уақытта шығаруын айтады. Жаппай есеп шешуді ұйымдастырудың алуан түрі болуы мүмкін.

2. Есепті жаппай ауызша шешу әсіресе орта сыныптарда кең тараған. Мұндай есептер негізінен ауызша орындауға болатын есептеулерді, тепе-тең түрлендірулерді және т.б. жаттығуларды қамтиды. Тәжірбиелі мұғалімдер, бүгінгі таңда, қысқа ауызша жаттығуларды жиі пайдаланады. Мұның өзі ойша шапшаң есептеуге машықтандырады. Сондықтан математиканы оқытудың барлық қажетті кезеңдерінде ауызша есептеулерге жүгінген жөн.

Ауызша орындайтын жаттығулар:

1. теорияалық білімді тексеруге арналған сұрақтар түрінде болыуы мүмкін:

«Көпмүшені бір мүшеге қалай көбейтеміз?», «у = x² фнукциясы графигінің түрі қандай», «у = x² фнукциясының графигі неліктен 0у осіне симметриалы болады» және т.с.с.

б)Теп-тең түрлендірулерді орындау, қарапайым теңдеулерді шешуді талап ету түрінде болуы мүмкін. Мұндай жаттығулар: өрнегін ықшамдаңдар, «2х-3=7 теңдеуін шешіңдер» түрінде беріледі.

в) зерттеуге арналған сұрақтар түрінде болуы мүмкін. Мәселен: «Модулы 4-тен артық сандарды сан осінде көрсетіңдер», = 0 теңдеуінің түбірі барма?», «а және 3а сандарының қайс артық». Бұл жаттығулердың, әсіресе, соңылары пайдалы, өйткені олар оқушлардың ойлау қызметін жандандрып, шамаларды салыстыруға машықтандырады.

Есептерді ауызша есептеу барсынды әртүрлі сызбаларды, сүлбелерді, анықтама мен көрнекті материалдарды пайдаланса, оқушылардың уақытын үнемдеуге, сабақты жанжандыруға көмектеседі.Көрнекіліктерді мұғалімнің өзі немесе оқушыларға дайындатуға болады.

2.1. Есептерді ауызша фронтальді шешу.

Бір ғана есепті бір мезгілде барлық оқушылар шығарады. Бұл әр түрлі болуы мүмкін.

а) Ауызша фронталь шешу – бұл 4-7 сыныптарда кең тараған жоғары сыныптарда онша көп қолданылмайды. Ауызша жаттығу теңбе-тең түрлендіру, есептер – сұрақтар жауаптың дұрыстығында ауызша дәлелдейді. Қазір 4-7 сыныптарда әрбір сабақта «бес минуттік» ауызша жаттығулар шығарады. Бұл арада ең маңыздысы тез ауызша есептейтін оңай шығарылатын әдістер.

3. Есепті жазбаша шешу.

Барлық оқушылар бір мезгілде есепті тақтада шешеді, мұнда не оқушы не мұғалім шешеді. Не мұғалім нұсқауы бойынша оқушы тақтада шығарады. Оны төмендегідей жүзеге асруға болады.

а) жаңа ұғым не жаңа тәсілдерді көрсеткеннен кейін тақтада есеп шығарады;

б) өзбетінше есепті барлық оқушылар шығара алмағанда;

в) бір есепті бірнеше әдіспен шешіп олардың тиімділерін таңдап алу қажет болғанда...;

г) өзбетінше шешкен есептерде кеткен қателерді талдағанда тақтада шешіледі.

Бір есепті әр түрлі вариант шешудің жолын қарастыралық. Кейбір тиімділерін талдау кезінде бірден қалдырады. Басқаларын жазады. Әр түрлі әдіспен шешуге бір мезгілде бірнеше оқушы тақтаға шығарады. Мұғалім тақтадағы барлық оқушыларға назар аударады. Бұл уақытты алады. Кейде әр варианттағы керекті жазуды мұғалім өзі орындайды. Мүмкін экранда алдын-ала жазылған шешімді көрсетеді.

Өзбетінше есепті жазып шешу.

Бұлайша жазып шешкенде оқушы шығармашылық жолмен ойлайды. Өзбетінше талдап, әр түрлі теориялық материалды есепке қажетінше қолданады. Өзбетінше шешудің көп пайдасы бар:

1. Оқуға деген белсенділігі артады, қызығушы шығармашылық бастамасы орнығады, ойлау қызметі дамиды.

2. Тақтадан көшірмей, оқушы өзі ойлауға мәжбүр болады, амалсыз сабаққа дайындалады.

3. Өзбетінше шешкенде уақыттан ұтады. Әр оқушы бағалауға болады.

4. Мұғалімге әр оқушының жұмысындағы жіберілетін қателерді жоюға мүмкіндік туады.

5. Мұғалім есепті ұсынады, кейбіреулеріне мұғалім кейбіреулеріне оқушы кеңес береді.

6. Есеп шешу үшін оқушы қажетті теориялық материалды өзбетінше оқып еске түсіреді, ұқсас есеппен мұғалім айтқан есептің шешу үлгісін талдап, сонан соң осыларға ұқсас есепті оқушы жеке өзі шешеді. Математикалық есептер шешуден ең жақсы өзбетінше есеп шешу үшін мұғалім есепті шешуге нұсқау береді. Оқушы орындайтын жұмыстардың қатаң ретін көрсетіп, артынан тексеру керек.

Математикалық есептердің шешімін түсіндіру.

1. Сыныптағы барлық оқушылар бір ғана бір ғана есепті шешді.

Бір оқушы есепті бастан аяққа оны түсіндіреді. Кейбір мұғалімдер мұндай түсіндіруді жатқа жаздырады. Бір оқушы шешкен есебін дауыстап айтады, ал қалғандары тыңдағанын дәптеріне жазады. Түсіндіретін оқушы өзі орындаған амалдарды, түрлендірулерді неге негізделіп жасағанын, басқаша ойларын, салудың нелерге негізделгенін түсіндіреді. Есептің әр жолы белгілі математикалық теорияға негізделетіні айтылу керек.

Мысалы, «Тізбектес натурал үш санның қосындысы жай сан бола алмайтынын дәлелдеңдер».

Бұл сандардың біріншісін n десек, қалғандары n+1, n+2. Бірінші санға қарағанда екіншісі, үшіншісі 2-ге артық.

Бұлардың қосындысын жазамыз, жақша ашамыз. Ұқсас мүшесін біріктіреміз, қосылғыштардың орындарын ауыстырғаннан қосынды өзгермейді

n+(n+1)+(n+2)=n+n+1+n+2=3n+3=3(n+1).

Соңғы алынған нәтижеден байқалатынындай n санының кез келген мәнінде жай сан бола алмайды. Мұндай түсіндірулер оқушыға көп пайда келтіреді. Бұлайша түсіндіргенде оқушының көбірек ойлануына, түрлендірулердің себептерін түсіндіруге мүмкіндік туады.

Есептер шешуді оқыту кезінде жекелей бабтың қажеттігі.

Есепті фронтальді шешу әрқашан көздеген мақсатқа жеткізе бермейді. Фронтальді шешкенде оқушылардың бәрі-бір есепті шешеді. Себебі бір оқушыға өте оңай болып ешбір қиындық келтірмейді, жаңалығы жоқ, ал екінші оқушыға бұл есеп өте қиындық келтіреді. Сондықтан әр оқушының жеке ерекшелігін есепке алу керек. Есептерді таңдағанда оны оқушылар қабілетіне қарай бір жүйеге салу керек, ол оқушылардың қабілетін дамытатындай болуы керек. Бұл арада мұғалімнің қызметі есепті шешуге дайындықты түсіндіру, сыныптағы әр оқушының қабілетіне, мүмкіндігіне қарай есептер шешуді ұйымдастыру. Есептер шешу кезінде оқушылардың мүмкіндіктерін есепке алу – нашар үлгерушілердің үлгерімі тәуірлер қатарына қосылуына мүмкіндік туады.

2. Есептер шешуде оқушылардың өзбетіндік жеке жұмысын ұйымдастыру.

Барлық оқушылар өзбетінше бір ғана есепті шешкенде мұғалім оқушылардың жеке басының ерекшеліктерін ескеруі керек, соған сәйкес есептерді тексергенде оларға көмек ұйымдастыруы. Оқушылар қабілетін және математикалық дайындығының қаншалық дәрежеде екенін есепке алу үшін оларға бірдей есеп ұсынбау керек, әр оқушының мүмкіндігіне қарай есеп ұсыну. (Молдава мектептерінің іс-тәжірибесі). Олар группаларға бөлінеді. Дегенмен, оқушылар қандай группаларға бөлінетінін алдын-ала білмеуі керек. Группа тұрақтанбауы керек.

3) Оқушы біліміндегі кемшіліктерді жою үшін оқушының жеке жұмысын ұйымдастыру.

Оқушы біліміндегі кемшіліктерді жоюда есептер шешу, бақылау есептерін үздіксіз орындау, сыныпта, үйде теориялық материалдар қажет болатын есептер шешу. Ол жүйелі түрде дәптеріне жіберген кемшіліктерін есепке алып, көрсетуі керек. Жақсы оқитын оқушылар жіберген қателігін өзі табатындай нұсқау айтуға болады.

Оқушылар жіберетін қателерге сай есептер таңдалып алынады. Қателердің себептеріне сай есеп таңдалады.

4) Оқушылардың үйде шешетін есептері.

Үйде шешуге ұсынылатын есептер мен жаттығулар оқушылардың бұдан бұрын өткен материалдарына сәйкес болуы керек. Бұл үй жұмысы сыныпта шешілген есеппен бірдей болсын деген сөз емес. Мұндай ұқсас есептердің пайдасы аз. Үй жұмысы оқушыны тек материалды қайталауға мәжбүр етіп қоймай, сонымен бірге бұдан кейінгі дамуында білім, білік, дағды қалыптастыруы керек. Математика мұғалімі үй жұмысына қажетті нұсқау береді, бірақ ондағы барлық қиыншылықтарды өзі айтып бермеуі керек.

Есептер шешу кезінде мұғалімнің оқушыларға беретін жалпы нұсқаулары.

1. Есептің қойылысы және оның мазмұнын меңгеру үшін беретін ұсыныстар (1-этап).

2. Есеп шешу жоспарын құру (2-этап).

3. Есепті шешу жоспарын іске асыру (2-3 этап).

4. Есеп шешімінің дұрыстығына талдау жасап тексеру (4-этап).

5. Жалпы нұсқаулардан дербес нұсқауларға.

6. Айтылған нұсқауларды есептер шешуге қолдану.

№ 6 лекция.

Тақырыбы: «Есеп шешу үрдісінің мазмұны (есеп шешу кезеңдері)» Есепті талдау және оның сүлбесін жазу. Жоспар

1. Есептеу толық шешімін табу үрдісі

2. Есепті талдау мен оны схемалық түрде жазу.

3. Есептің шартын тұжырымдау.

4. Есепті талдаудың жалпы жоспары

1.Есептеу толық шешімін табу үрдісі

Заман өзгерісіне қарай мектептерде қойылатын талап та, ондағы оқыту және тәрбиелеу әдіс-тәсілдері де өзгереді. Қазіргі таңдағы еліміздегі білім беру жүйесінің ең басты міндеті-жас ұрпақтың білім деңгейін халықаралық дәрежеге жетелеу. Мектепке соңғы уақытта келген жаңашылдық бастамалар мұғалімдердің белсенді өз тәжірибелерін сыни тұрғыдан қайта қарап, өзі айналысып жүрген істерінің нәтижесінің мақсатқа сай орындалуын оймен зерттей білуге, өз кәсіби өмірбаянындағы салмақты жүктерді саналылықпен алмастыра алуға ынталандырады.

Қазіргі математиканы оқыту әдістемесі оқушының танымдық қызметі мен ойлау жүйесінің арақатынасын анықтай түсуде. Ол оқушының дербестігін, танымдық қажеттілігін қанағаттандырумен қатар, интелектуалдық ойлау мүмкіндіктерін қалыптастырады. Оқушы қабілетіне дұрыс көзқараспен қарау, оқушының алғаш өз бетінше жұмыс жасауына жағдай жасау оқу-тәрбие ісінде жетістіктер береді.

Оқыту үрдісінде есеп шығаруға оқушыларды үйрету мақсат десек, ал белгілі бір типтегі есептердің шығарылуын қарастыру қандай да бір математикалық материалды меңгеруге әсерін тигізетін әдіс болып табылады. Сондықтан оқыту барысында оқушыларды есеп шығаруға үйретуге көп көңіл бөлінеді. Соңғы кезге дейін есеп шығаруға үйретудің бірден-бір тәсілі белгілі бір түрдегі есептерді шығарып көрсету ғана болатын. Сондықтан оқушыларға арналған есеп шығару кұралдары жауабы және оған байланысты кейбір нұсқаулары бар есептер жинағы болып келді. Осыған орай, оқушыларды есеп шығаруға үйретудің әдістемесі мен жалпы тәсілін үйретуге арналған көптеген құралдар шығуда.

Есеп шығарудың жалпы білігі мен дағдысын қалыптастырудың қиындығы оқушыларды есеп шығару барысындағы іс-әрекеттеріне жүйелі де тиянақты талдау жасалып отырмауына, оқушылар шығаратын есептердің барлығына ортақ жалпы істің анықталмауына, сондай-ақ белгілі бір типтегі есептерді шығаруға үйретуді неден бастау керектігін, ондағы жүйелілік пен сабақтастықтық қалай болатынын анық білмеуге байланысты екенін мектеп тәжірибесі көрсетіп отыр. Сондықтан, математиканы оқыту үрдісін жетілдіру оқушылардың танымдық белсенділігі мен ізденімпаздығын арттыруға негізделген. Оқу танымдық қызметі барысында оқушылар қажетті көлемдегі білімді игеріп қана қоймастан, танымдық қабілеті мен шығармашылық ойлауы да дамытылады.

2.Есепті талдау мен оны схемалық түрде жазу

Танымдық қызметті арттырудың бір жолы берілген материалдың теориялық мәнін, өмірлік тәжірибеде қолданысын ашып беру болып табылады. Егер оқушы берілген материалдың өмірлік тәжірибеде кеңінен қолданылатынына және әрбір сабақтың өткен материалдарымен байланысты екеніне көз жеткізсе, білімге деген ынтасы артады. Мысалы: көбейту мен бөлуді қысқаша көбейту формулаларын толығымен түсінбей, келесі тарауларда оқытылатын алгебралық түрлендірулерді шешу мүмкін емес.

Оқушы бойында танымдық қызығушылықты арттыру үшін мына мәслелерді есте ұстау керек:

• материалдық сілтеме тағайындау;

• алдын ала қажетті біліми мәліметті беру;

• оқушыны психологиялық тұрғыда дайындау;

• мұғалімге, пәнге дұрыс көзқарас

• пәнге саналы қатынасы және берілген білімнің тәжірибелік мәні мен мүмкіндіктерін игеру

Республиканың және шетелдің психологтары ойлаудың проблемалық жағдайдан туындайтындығы және оны эксперимент арқылы шешуге болатынын дәлелдеген. Ойлау үрдісі және оның нәтижелері өзара байланысты. Психология ғылымында математикалық қабілеттілік проблемалардың комплексі ретінде қарастырылады. Осы заманғы психологиялық зерттеулерде математикалық қабілетке қатысты:

• есептер шешуге байланысты ойлау тәсілдерінің ерекшеліктерін анықтауға ұмтылу.

• математикалық қабілеттің құрылымына талдау жасауға ұмтылу сияқты екі бағыт бар.

Логикалық ойлау математикалық ой қорытудың негізін құрайды, осы тұрғыдан алғанда есептер шешу процесі бұрыннан белгілі проблемаларға жаңа салдарлар жасау болып табылады. Қарастырылған пәнге байланысты бұрын алған білімдерге сүйеніп негізделген салдарлар жасай аламыз. Бірақ математикалық ой тұжырымы тек логикалық жағынан тұрмайды. Математикалық қызметтің жемісті болуы үшін тек логикалық қорытындылардың жетімсіз болатыны туралы ірі математиктер Декарт пен Галуа көрсетті. Кез келген жаңа теореманы ашудың себебі ол алғашқы аксиомаларға байланысты бола отырып дәлелденген, олай болса осы аксиомаларын шығарып ойды қорытуға болатын сияқты. Бұл тек дайын ғылымға қарап отырған сияқты болып шығады. Ал шынында да дәлелдеушілер салыстырады, мәселенің барлық жақтарын қарастырып, шындыққа қол жеткізеді.

Өмірге, күнделікті тұрмысқа және келешек өндірістік технологияға қажетті тәжірибелік мазмұндағы математикалық есеп деп оның басқа пәндермен байланысын ашып көрсететін және қазіргі өндірістегі қызмет ету саласында еңбек ету айла-шараларын қолдана білуге көмектесетін есептерді айтамыз.

3.Есеп тұжырымдау.

Оқушыларға ой тудыратын математикалық есептерді талдап қарастырғанда оның мәселесін шешуге ыңғайылы әрі көрнекті болатын жағын ойластырған жөн. Оларды мына төмендегідей етіп жіктеуге болады:

• есептің ғылыми дүниетанымдық және тәрбиелік құндылығы;

• есепте қолданылатын математикалық емес матеиалдар мүмкіндігі;

Математикалық есептерді шығара білуге үйрету жане одан әрі оған дағдыландыру — мұғалімдер алдында тұрған өте қиын да жауапты жұмыс. Әр оқушының математикаға деген ұқыптылығы мен зейінділігі түрліше, ал математикалык есептердің саны шексіз көп. Есеп шығаруға үйрету мен дағдыландыру көбіне сыныпта сабақ өту кезінде болатындықтан, барлық оқушыларды есеп шығарудың жалпы әдіс-тәсілдерімен карулаңдыру керек. Мұны іске асыру үшін олардың есеп шығару процесіндегі іс-әрекеттерін басқарып, жұмысты белгілі бір жүйемен жүргізген жөн.

Оқушыларды есептер шығара білуге үйрету процесі шығармашылық сипатта болуға тиіс, яғни мұғалім ұсынған әдісті сол күйінде қолдануға жол бермей, есепті шығару жолын іздеп табу мұғалімнің басшылығымен орындалатын оның шығармашылық жұмысының жемісі ретінде болғаны жөн. Ол үшін есеп шығару үрдісінің құрылысын білу кажет.

Барлық есептер үшін мына кезеңдерден тұратын шешу кұрылысы карастырылады:

• есеп  шартымен таныстыру (есеп шартын шешуші системаның қабылдап меңгеруі; іске кажетті хабарларды шешуші системаның есінде сақтау);

• есеп шығарудын жоспарын құру (есеп шығарудық әдіс-тәсілдерін таңдау, орындалатын түрлендірулердің құрамын және реттіліктерін анықтау);

• шешуді орындау (енген хабарларды қорытынды хабарларға айналдыру);

• есеп шешуінің дұрыстығын тексеру (қорытынды жасау; шыққан шешімді бағалау; басқа шешуді іздестіру).

Әрбір кезең белгілі бір амалды орындау арқылы жүзеге асырылады. Атап айтқанда:

• бағытты анықтау — іс-әрекет мақсатының сипаттамасын айқындау, түрлендірулер қолданылатын объектінің қасиеттерін атап көрсету;

• жоспарлау — орындалатын түрлендірулердің кұрамы мен реттілігін анықтау;

• атқару — осы түрлендірулерді орындау;

• бақылау — іс-әрекет мақсатының орындалуын тексеру.

Есеппен танысқаннан бастап оның толық шешімін алғанға дейінгі процесті қарастыратын болсақ, онда бұл процесс бірнеше кезеңнен тұратынын көреміз. Енді сол кезеңдерді анықтайық.

Сонымен есеп шығару процесін сегіз кезеңге бөлуге болады:

• есепті талдау;

• есепті схемалық түрде жазу;

• есепті шығару тәсілін іздестіру;

• есеп шығаруды жүзеге асыру;

• есеп шығарылуын тексеру;

• есепті зерттеу;

• есеп жауабын тұжырымдау;

• есеп шығарылуына талдау жасау.

Бұл келтірілген схемадан есеп шығару процесі күрделі және әр алуанды үрдіс екендігі байқалады. Мысалмен көрсетейік.

Е с е п. Екі жұмысшы бірігіп жұмысты 12 сағатта бітірді. Егер ең алдымен бірінші жұмысшы жұмыстың тең жартысын істеп, ал екінші жұмысшы қалған бөлігін бітірсе, он-да барлық жұмыс 25 сағатта бітеді. Әрбір жұмысшы осы жұмысты қанша уақытта бітірер еді?

1. Есепті талдау. Есепте екі объект туралы сөз болып тұр. Олар: бірінші және екінші жұмысшы. Олардың жұмыс істеу шапшаңдығы әр түрлі, егер жұмыс істеу шапшаңдығы бірдей болса, онда бірінен кейің бірі істегенде, барлық жұмысты 24 сағатта (12 сағ-2) бітірер еді. Есепте бұл шапшаңдықтар берілмеген. Оны табудың қажеті де жоқ. Бірақ жұмысшының жұмысты қанша уақытта бітіретіндігін, яғнн уақытты табу қажет.

2.Схемалық түрде жазу. Жұмыс көлемін кесіндімен белгілесек, онда схемалық жазу былай болады:

1 мен 2 бірігіп, 12 сағ

_____________________

1-ші содан соң 2-ші 25 сағ

3. Есепті шығару тәсілін іздестіру. Әрбір жұмысшының жұмысты қанша уақытта бітіретінін табу керек. Жұмыс көлемі белгісіз. Жұмыс колемін I өлшем деп алсақ, онда екі жұмысшы бір сағатта жұмысты бөлігін бітіреді. Бұл, екеуінің, жұмыс істеу шапшаңдығының қосындысы. Жұмысты бітіру уақытына кері шама, бұл жағдайда жұмыс істеу шапшаңдығы болады.

Бірінші жұмысшының жұмысты бітіру уақытының жартысы мен екінші жұмысшының жұмысты бітіру уақытының жартысының (себебі олар бірінен соң бірі барлық жұмыстың жартысын ғана істен бітірді) қосындысы 25-ке тең болады.

6. Есепті зерттеу. Есепте айтылған мағынадан шығып тұр, мұндағы QUOTE Бұлар нольге тең болғанда есеп шартының мағынасы болмайтындықтан, біз есеп шығару процесінде х пен у нольге тең болмауы керек деп айқындап жазғанымыз жоқ.

Есеп шығару қорытындысында х=30, у = 20 және х = 20, у = 30 түрінде екі жауап шықты. Шындығында бұл бір ғана жауап, себебі жұмысшының біреуі жұмысты 30 сағатта бітірсе, екіншісі 20 сағатта бітірген. Олардың қайсысын бірінші десек те, оның ешбір мағынасы өзгермейді.

7. Жауабы: Жұмысшылардың біреуі (мүмкін біріншісі, мүмкін екіншісі) жұмысты 30 сағ, ал екіншісі — 20 сағ бітіреді.

8.Есептің шығарылуына талдау жасау. Бұл есептің шығарылуы екі белгісізі бар екі теңдеулер системасын шешуге келтірілді.

Жұмыс көлемін бір өлшем деп алдық, оны г әрпімен белгілесек, онда г системаның екінші теңдеуінің алымында болады да қысқарып кетеді.

4.Есепті талдау жоспары

Математикалық есептерді шешудің соңғы қорытындысы кезеңі.

Есеп шешуде оның жауабын алу маңызды емес. Есепті іздеу процесі информацияны алу маңызды. Соңғы кезеңде ойлану, орандау, мұны басқа есептерге қолдану соңғы этапты мына схема түрінде көрсетуге болады.

Лекция 7

Тақырыбы: «Оқушының математикалық ойлауының дамуы және

математикалық есептердің ролі.

Жоспар:

1. Математикалық ойлауды дамытудың проблемалары

2. Оқыту процесіндегі математикалық ойлаудың ролі

3. Дамушы математикалық ойлаудың жалпы сипаттамасы

4. Математикалық ойлаудың структурасы туралы.

5. Есептер шешу арқылы оқушының ойын дамыту

Математикалық ойлауды дамытудың проблемалары.

Математикалық ойлауды дамыту орта мектептегі ең маңызды мәселелердің бірі, яғни ойлауды тәрбиелеу.

Орта мектеп математикасының мазмұнының өзгеруіне байланысты «Математикалық ойлау» ұғымының көлемі кеңейіп, оқыту процесінде ерекше роль атқаратын болды. Оқыту жүйесі мен оқушының ақыл ойының дамуында белгілі бір заңға бағынатын өзара тығыз байланыс болады. Бұл заңдылық педагогикалық психологияның қарастыратын маңызды мәселесі болып табылады.

Күнделікті өмір практикасы мұғалімнен оқушылардың математикалық ойлау қабілетін дамытуды талап етеді. «қандай ойлау – математикалық?» «Оның қандай негізгі сипаттары бар?» Бұл сұрақтың шешімі әлі жоқ.

Оқыту процесіндегі математикалық ойлаудың ролі.

Оқушыларға математикалық білім беру өте күрделі үрдіс, ол мынадай негізгі компоненттерден тұрады:

а) оқушылар белгілі бір математикалық фактілермен идеялар жүйесіне ие болады;

б) белгілі бір білім, білік дағдыларын меңгереді;

в) математикалық ойы дамиды.

Оқыту процесінде оқушылардың математикалық ойы стихиялық түрде дамиды деп есептелініп келген.

Ғалым психологтардың көрсеткеніндей математикалық ойлау оқушылардың таным қызметтегі маңызды компонент болып қоймай, саналы түрде бағытталған ой дамуын математикалық білім, білік және дағдылар жүйесін тиімді түрде қалыптастыруға болмайтынын көрсетіп берді.

Психолог А.Н. Леонтиев «Оқыту процесі және оқушының ақыл-ойының дамуы тығыз байланыста болады».

Бала оқып, өзін қаншалықты дәрежеде жетілдіргенде оның ақыл-ойының дамуы салыстырмалы түрде өзіндік ерекшелікке ие болады.

Математикалық ұғымдар оқушыларда танымдық процестен басқаша қалыптаспайды, оқытудың жекелеген кезеңдерінде біртіндеп ойлау процесін толықтырады. Басқаша айтқанда математикалық ойы нашар дамыған оқушы белгілі-бір математикалық идеяны, ұғымды меңгере алмайды, ал қабілетті оқушылар фактілерді тек формальді түрде есіне сақтайды.

Ұғымдарды меңгеру үшін белгілі-бір ақыл-ойдың әрекетінде оны саналы түрде қайталап, ақыл-ойдағы сын қалыптастыру керек.

Есеп шығару процесінде де осылай, есептің шығарылу жолын зерттеп, белгілі бір әдіс-тәсілдерді ойлап табамыз, сонан соң оның педагогикалық тиімділігі, т.б. эксперимент арқылы тексереміз. Яғни ойлаудың нақты әдісі, есептеу, табу, белгілі бір амалдардың бірлігіне, байланысына қолданылады. Математикалық ойдың дамуы оқушылардың қабылдаған математикалық амалдары мен тәсілдерінің байланысын жаңа байланыстарды есептер шығаруға қажет, жаңа әдіс-тәсілдерді, сол арқылы жаңа білім алуға көмектеседі.

Бір ғана есепші бірнеше оқушы шығарып жатыр. Мұғалім бірдей бір ғана нұсқау айтқанымен әр оқушының өзіндік ойлауы болғандықтан, ол нұсқау әр оқушыға түрліше әсер етеді.

Оқушы неғұрлым нұсқауды тез қабылдаса, оның тез терең ойланғаны, ал баяу шығарса.