Бір айнымалыға тәуелді екінші дәрежелі теңсіздіктер
не
(8)
түріндегі
теңсіздіктерді бір айнымалыға тәуелді
екінші дәрежелі теңсіздіктер деп атайды.
(8) теңсіздіктерді шешу үшін
квадраттық функцияның қасиеттері
қолданылады. Бұл үшмүшеліктің графигі
коэффициентіне және
дискриминантқа байланысты.
теңдеуінің түбірлерін
деп белгілейік.
болсын.
жағдайды қарастырайық. функциясының графигінің тармағы жоғары қарайды.
Егер
болса, онда
және
болғанда
(9)
болады.
Ал,
да
(10) болады.
Егер
болса, онда
барлық мәнінде
(11) болады. Бұл жағдайда
теңсіздігінің шешімі жоқ.
Егер
болса, онда
-тің
кез келге мәнінде
(12).
болады.
Бұл жағдайда
теңсіздігінің шешімі жоқ.
жағдайды қарастырайық.
функциясының графигінің тармағы төмен
қарайды.
Егер болса, онда және болғанда (13) болады, да (14).
Егер болса, онда барлық мәні үшін (15), теңсіздігінің шешімі жоқ.
Егер болса, онда -тер үшін (16) болады. Бұл жағдайда теңсіздігінің шешімі жоқ.
7-мысал.
теңсіздігін шешу керек.
Шешуі:
Бұл есепте
.
теңдеуінің түбірлері
(10) теңсіздік бойынша
болғанда
болады. Сонымен, теңсіздіктің шешімі
аралығы.
8-мысал.
теңсіздігін шешу керек.
Шешуі:
теңдеуінің еселі түбірі бар.
Бұл есеп жағдайында
,
(11) формуланың негізінде
-ден басқа барлық
-тердің
мәні үшін
теңсіздігі дұрыс болады.
9-мысал.
теңсіздігін шешу керек.
Шешуі:
теңдеуінің түбірлері
(13)
формулаға сәйкес
және
болғанда
болады.
10-мысал.
теңсіздігін шешу керек.
Шешуі:
онда
нақты түбірлері жоқ.
функциясының графигі ОХ осін қимайды,
ол тұтасымен ОХ осінің жоғары жағына
орналасады.
–тің
барлық мәнінде
Демек, кез келген
үшін
.
Олай болса,
теңсіздігін шешімі жоқ.
11-мысал.
теңсіздігін шешу керек.
Шешуі:
теңдеуінің түбірлері
(14)
формулаға сәйкес айнымалының мәні
болғанда
теңсіздігі дұрыс орындалады, яғни
теңсіздіктің шешімі
аралығы.
12-мысал.
теңсіздігін шешу керек.
Шешуі:
теңдеуінің еселі түбірі бар, ол
Бұл арада
Демек, (15) формула бойынша,
-ден
басқа мәнінде
болады.
13-мысал.
теңсіздігін шешу керек.
Шешуі:
теңдеуінің нақты шешімі жоқ. Өйткені
функциясының графигі ОХ осін қимайды,
график тұтасымен ОХ осінің үстінгі
жағына орналасады. Кез келген
үшін
Демек,
–тің
кез келген мәні үшін
.
Теңсіздіктің шешімі
аралығы.
14-мысал.
теңсіздігін шешу керек.
Шешуі:
Берілген теңдеу
Себебі
Функция графигі ОХ осін
нүктесінде жанайды. Парабола тармағы
жоғары бағытталған.
Берілген теңсіздіктің шешімі
.
15-мысал.
теңсіздігін шешу керек.
Шешуі:
теңдеуінің нақты түбірлері жоқ, өйткені,
Функция графигі ОХ осімен қиылыспайды,
график тұтасымен ОХ осінен төмен
орналасады не
Демек,
-тің
барлық мәндері үшін
теңсіздігінің шешімі
шектеусіз аралығы.
16-мысал.
теңсіздігін шешу керек.
Шешуі:
теңдеуінің еселі түбірі бар, ол
Функция графигі
нүктесінде ОХ осін жанайды,
Берілген теңсіздіктің шешімі
.
4-мысал.
теңсіздігін шешу керек.
Шешуі:
Берілген теңсіздік
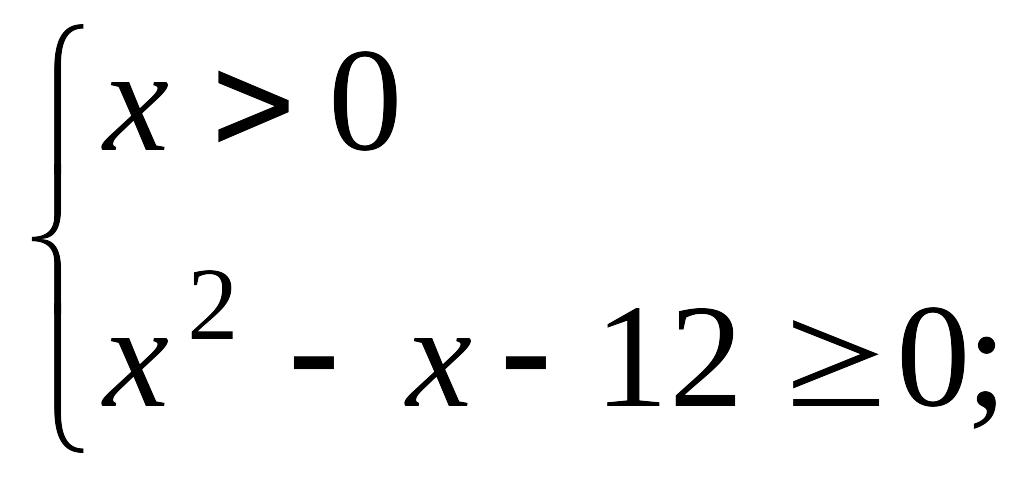
теңсіздіктер жүйесінің жиынтығымен
мәндес. Бірінші жүйені шешсек,
теңсіздігі
–тің
мәнін қанағаттандырады.
болғандықтан бірінші жүйенің шешуі
аралығы. Екінші жүйеден
бұдан
.
Себебі
,
онда осы жүйенің шешуі
аралығы. Сонымен
5-мысал.
теңсіздігін шешу керек.
Шешуі:
Түбір дәрежесі тақ
сан, олай болса, (4) теңсіздік бойынша
теңсіздіктің екі жағын куб дәрежеге
шығарамыз, түрлендірсек
.
Квадраттық теңсіздікті шешсек,
6-мысал.
теңсіздігін шешу керек.
Шешуі:
бұл түріндегі теңсіздік, түбір көрсеткіші
жұп. Теңсіздік
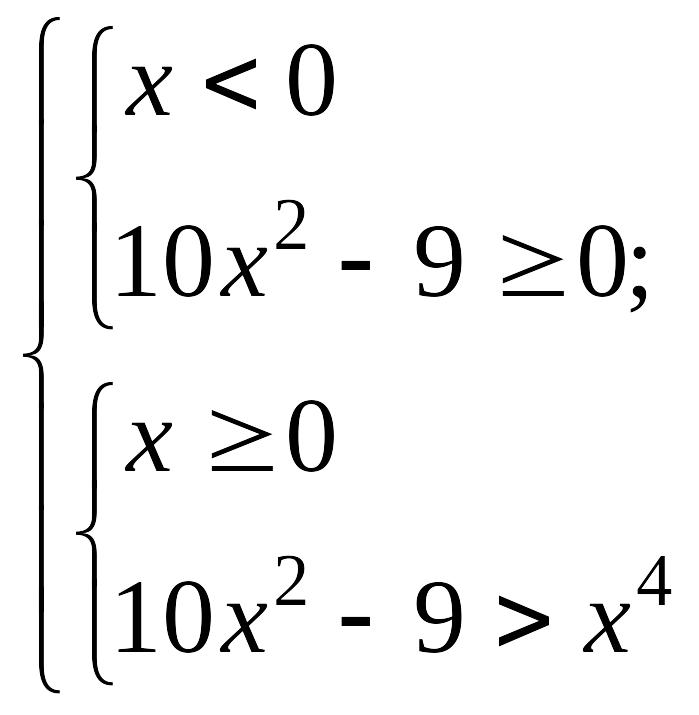теңсіздіктер жүйесінің жиынтығымен
мәндес. Бірінші жүйені қарастырайық.
Бұдан
және
.
болғандықтан бұл жүйенің шешімі
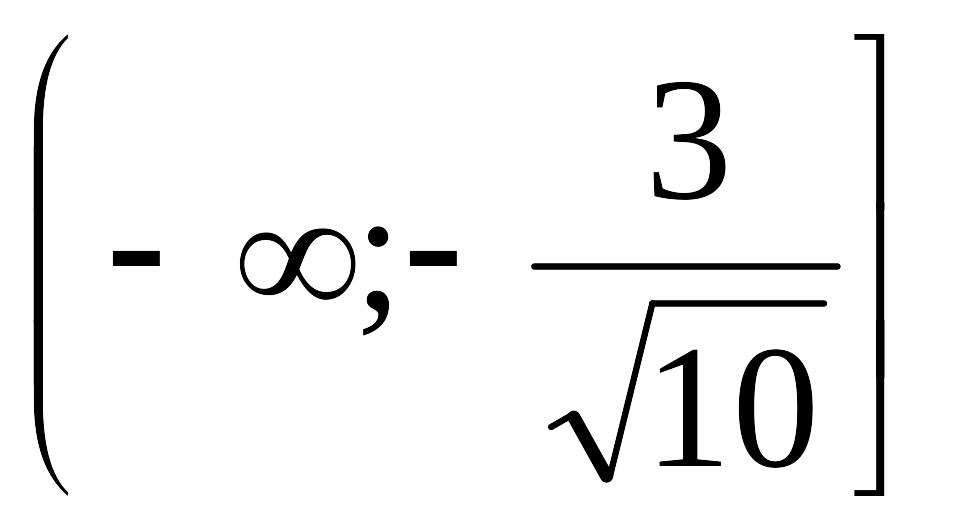аралығы. Екінші жүйеден
десек,
Мұның шешуі
демек,
теңсіздігінің шешуі
Бұл арада
болғандықтан екінші жүйенің шешуі
3-мысал.
теңсіздікті шешу керек.
Шешуі:
Теңсіздік
болғанда анықталады. Сонымен,
.
Теңсіздіктің анықталу аймағы
аралығы.
формуласын пайдаланып, берілген
теңсіздікті
түрінде жазамыз, бұдан
Бұл квадрат теңсіздік
және
болғанда орындалады. Анықталу аймағын
ескерсек, теңсіздік шешімі
аралығы.
4-мысал.
теңсіздігін шешіңдер.
Шешуі:
Теңсіздіктің анықталу аймағы
яғни
екенін ескеріп,
Бұдан
Егер
онда
демек,
бұдан
Егер
,
онда
демек,
не
не
Сонымен, теңсіздіктің шешімі
Жоғары дәрежелі теңдеулерді шешу
3-мысал:
теңдеуін шешу керек.
Шешуі:
болғандықтан теңдеудің екі жағын да
-қа
бөліп, оны мынадай түрге келтіреміз.
белгілеуін
енгізейік, келесі жүйені шешіп
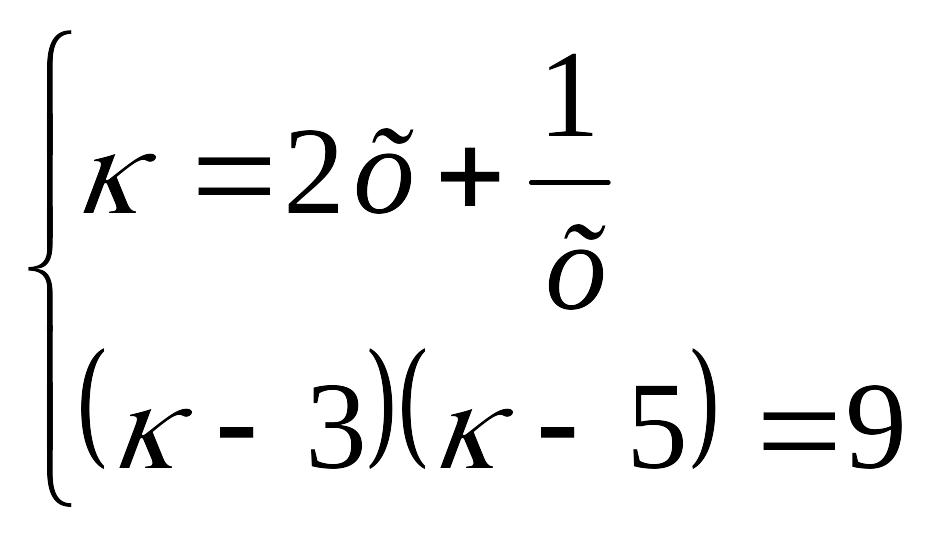
таптық.
3-мысал:
теңдеуін
шешу керек.
Шешуі:
болғандықтан,
теңдеудің сол жақ бөлігіндегі бөлшектің
алымын да бөлімін де
ке бөліп,
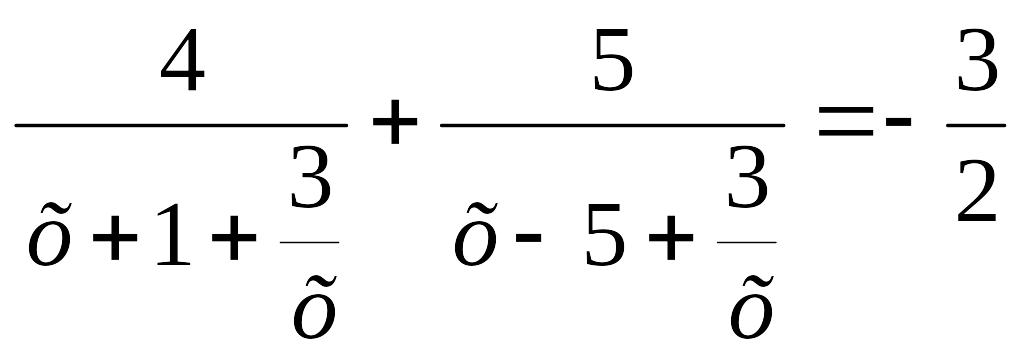теңдеуін аламыз.
белгілеу
енгізсек,
болады,
сонда
түріндегі
теңдеуінен
теңдеуі түріне келтіреміз.
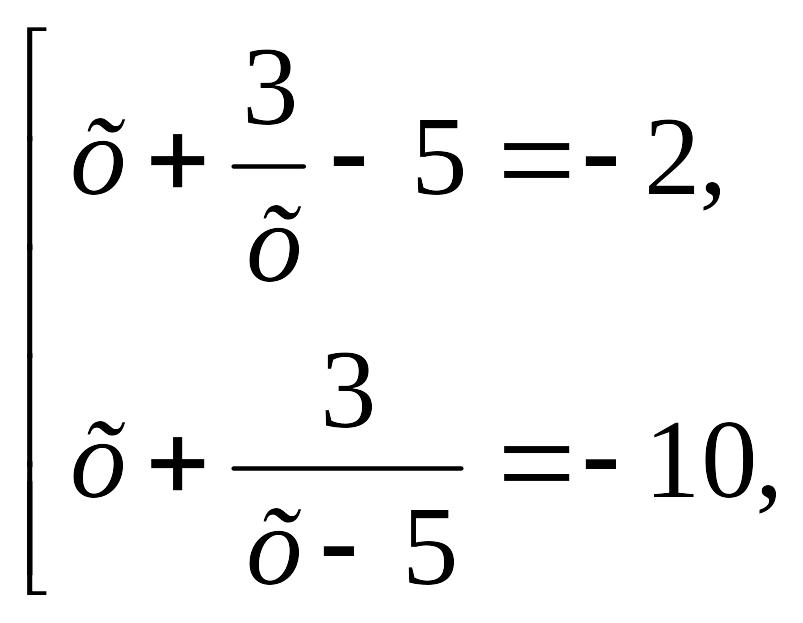
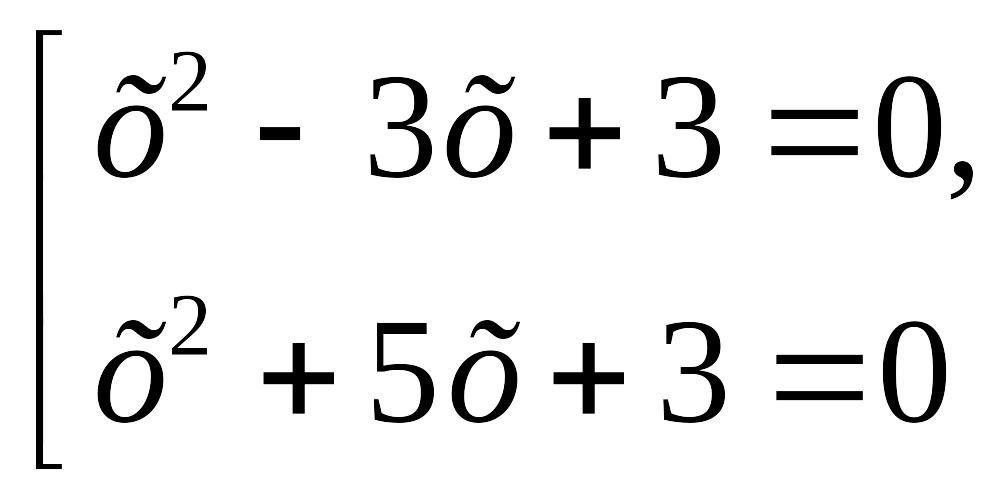
Жауабы:
5-мысал:
теңдеуін шешк керек.
Шешуі:
белгілеуін енгізсек,
түрінде
болады.
Ал,
теңдеуінің әрқашан да екі түбірі
болатындығын байқаймыз.
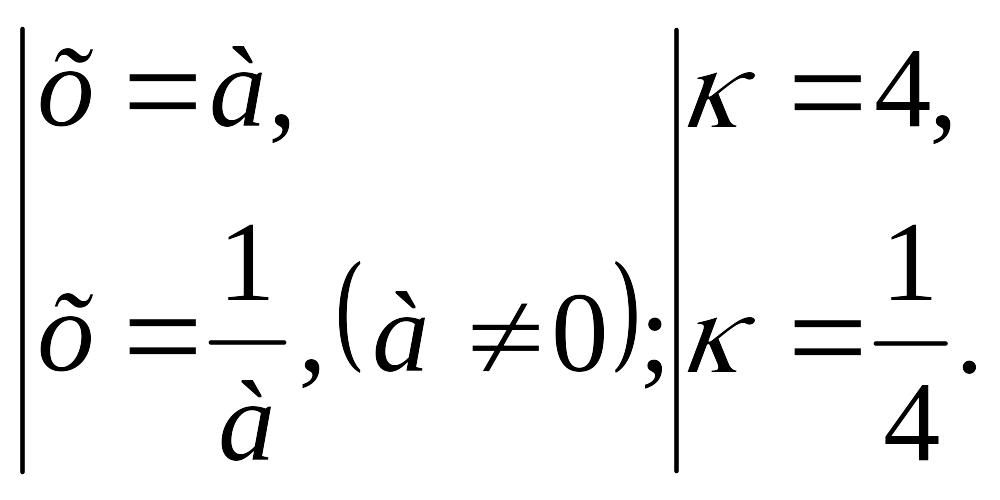
1)
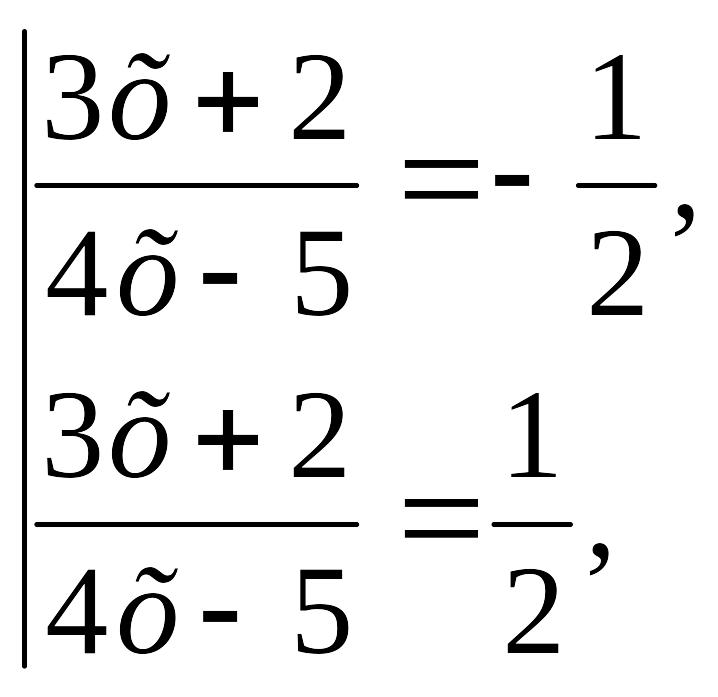
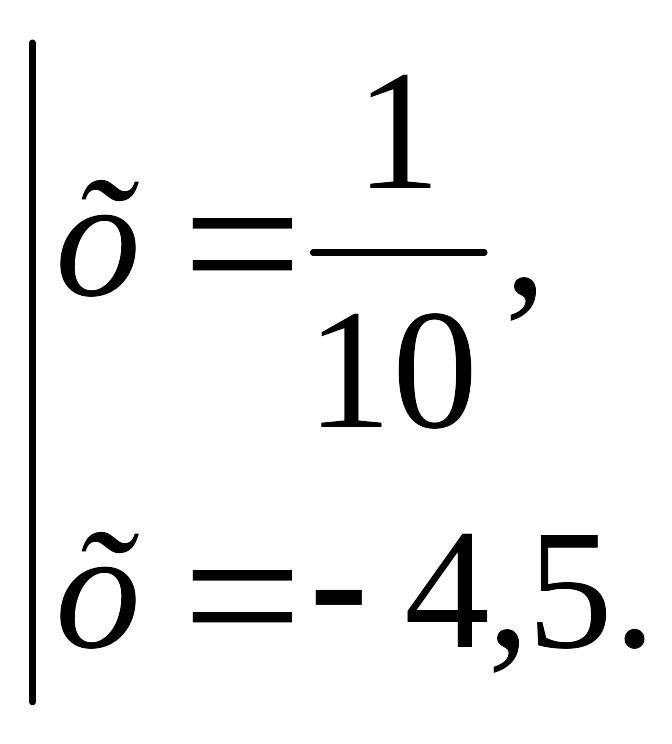
2)
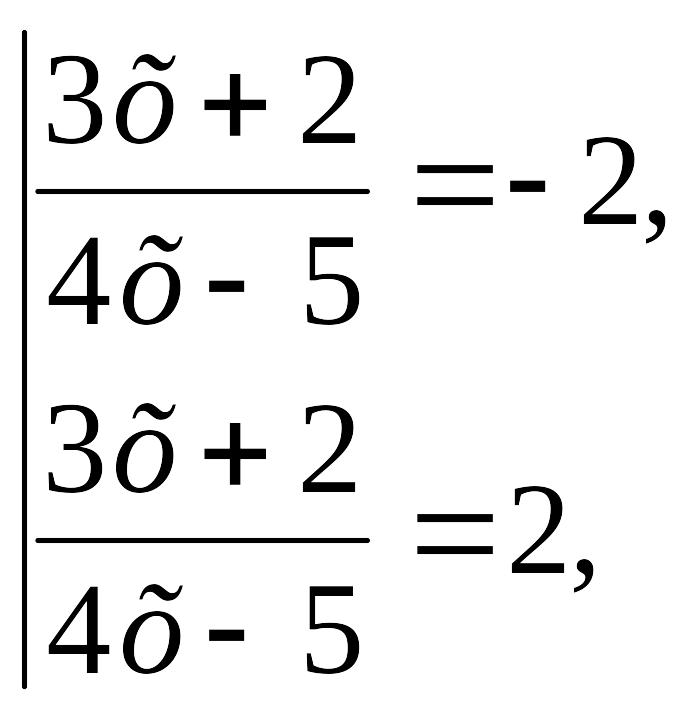
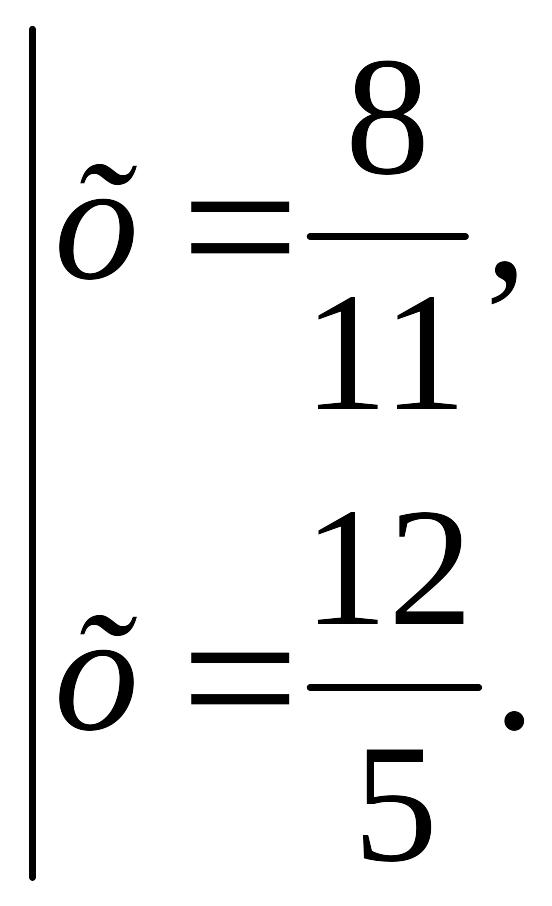
Жауабы:
6-мысал:
теңдеуін
шешу керек.
Шешуі: теңдеу төртінші дәрежелі симметриялы теңдеу. болғандықтан теңдеудің екі жағын -қа бөліп, мынадай мәндес теңдеуге келтіреміз.
белгілеуін
енгізгеннен кейін берілген теңдеуге
мәндес жүйеге келтіреміз.
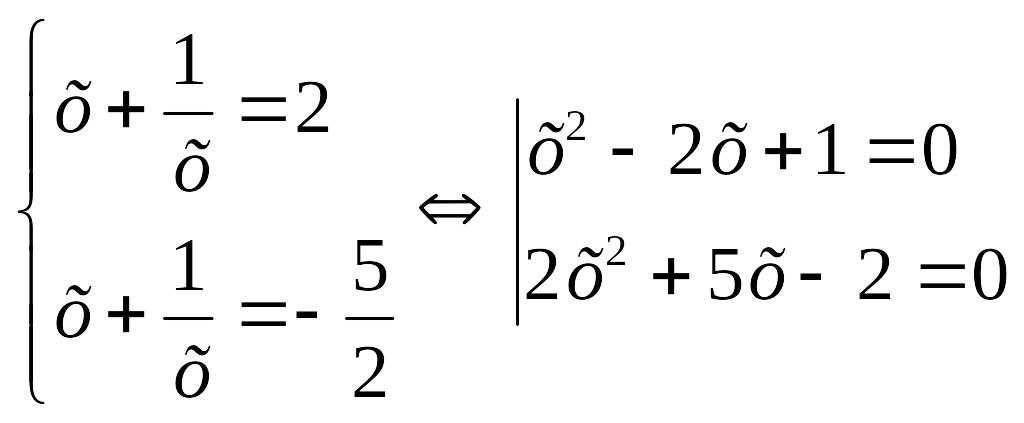
Жауабы:
4-мысал:
теңдеуін шешу керек.
Шешуі:
алмастыруының көмегімен (симметризациялау
әдісі)
теңдеуіне немесе
теңдеуі түріне келтірілді. Осы биквадрат
теңдеуді шешіп,
түбірлерін тауып, одан әрі қарай
айнымалысына
табамыз
Жауабы:
7-мысал. Математикадан бақылау жұмысын жазған сынып оқушыларының 12%-і есептерді мүлде шығара алмады, 32%-і шығарған есептерді қателер жіберді, ал қалған 14 оқушы дұрыс шығарды. Сыныпта қанша оқушы болды?
Шешуі:
12%+32%=44%, 100%-44%=56%,
.
Мәтіндік есептер
8-мысал. Тік бұрышты формалы бақша участогінің ұзындығы оның енінен 10 м артық. Осы участогтің ауданы 1200 м2 болса, онда оның қоршауының ұзындығы қандай?
Шешуі:
9-мысал. 6 палатка тігу үшін ені 1,2 болатын 120 м брезент керек. Ені 1,5 болатын сондай 4 палатка тігу үшін неше метр брезент керек?
Шешуі:
;
10-мысал. Аэропортта 880 жолаушы ұшақ күтіп тұр. Олардың 35%-і еркектер. Әйелдер мен балалардың жалпы санының 75%-ін әйелдер құрайды. Аэропортта қанша әйел және бала болғанын табыңыз.
Шешуі: х- еркектер, у- әйелдер, z- балалар.
;
ІІ. 1) Проценттер
Берілген
санның жүзден бір бөлігін процент санның
бір проценті
- ден белгіленеді. Мысалы,
;
;
;
;
.
Проценттің бір-бірінен өзгеше үш түрі бар:
берілген санның белгілі процентін табу;
проценті бойынша санның өзін табу:
екі санның процентік қатынасын табу.
1-мысал:
Цех бір күнде
бұйым жасайды. Егер еңбек өнімділігі
артқан болса, онда қанша бұйым артық
жасалған?
Шешуі:
(бұйым)
2-мысал:
Еңбек өнімділігін
-ке
арттырудың нәтижесінде бір күнде
бұй- ым жасалатын болды. Бұрын бір күнде
қанша бұйым жасалған?
Шешуі:
(бұйым)
3-мысал: Цех күніне бұйым жасайды. Бұйым жасаудың техникасын жетілді- рудің нәтижесінде күніне бұйым жасайтын болды.Еңбек өнімділігі қанша про- центке өскен?
Шешуі:
Мұндай
есептерді шешкенде өзімен салыстыруға
болатындай басқа сан –ды бөліп алады.
Бөліп алынған сан
болуы тиіс.
Процент
санын
-әріпімен
белгілейміз. Осы есептің жағдайында
үшін 180 санын алады, ал
саны үшін -
Сонымен,
Бұл
арада бұйым санымен оған сәйкес процент
саны тура пропорционалдық бай – ланыста
болады, сондықтан
,
Соңғы
еңбек өнімділігі бұрынғының
- ін құрайды. Сондықтан еңбек өнімді-
лігінің артуы
ІІ. 2) Процентке байланысты есептер
1-мысал:Кептіргенде
саңырауқұлақ өзінің массасының
-ін
жоғалтады. Қанша жас саңырауқұлақтан
кептірілген 1 кг саңырауқұлақ алуға
болады?
Шешуі:
Кептірілген
кезде саңырауқұлақтың бастапқы массасының
і
қалады. Демек,
2-мысал:
Сыныптағы оқушылардың
-і
бақылауды орындай алмады.
-нің
қателері бар, қалған
оқушы бақылауды қатесіз орындады.
Сыныпта неше оқу -шы бар?
Шешуі:
Сыныптағы
оқушылар саны
,
онда есеп шартына сүйеніп,
,
теңдеуін құрамыз, бұдан
.
3-мысал:
Бір жұмысшының еңбек ақысын екі рет
бірдей процентке арттырғанда, ол
есе өсті. Еңбек ақы әр кез қанша процентке
өсті?
Шешуі:
алғашқы
еңбек ақы,
ізделінді
процент саны, еңбек ақы бірінші рет
өскенде
,
екінші рет өскенде
.
Есеп шарты бойынша
,
,
;
бұл арадан
.
4-мысал:
Төртініші разърядты жұмысының жалақысы
үшініші разърядты жұмы -сының жалақысынан
көп. Төртінші разърядты жұмысшыға
қарағанда үшінші разърядты жұмысшы
қанша процент аз жалақы алады?
Шешуі:
-
үшінші
разърядты жұмысшының жалақысы болсын,
онда төртінші разърядты жұмысшының
жалақысы
.
Енді
санына
қарағанда
саны
қанша процент аз?
.
5-мысал: Тауардың бағасын алдымен -ке арттырды, одан соң -ке кеміт- ті. Тауардың алғашқы бағасы қанша процентке өзгерді?
Шешуі:
Тауардың
алғашқы бағасы
,
бағасын арттырғаннан соң
,
ал бағасын кеміткеннен соң
.
Яғни осы өзгерістердің салдарынан
алғашқы бағасы
-ке
кемиді.
6-мысал:
Жас шөптің ылғалдылығы
,
құрғақ шөптің ылғалдылығы
.
тонна
жас шөптен қанша кептірілген шөп алуға
болады?
Шешуі:
т
жас шөптің массасы болсын.
-кептірілген
шөп массасы. Әр жағдайда да масса судан
және құрғақ заттан тұрады. Мынадай схема
жасауға болады:
Су
(
)
-
Құрғақ
зат (
)
Массасы .
Су ( ) -
Құрғақ
зат (
)
Массасы .
Құрғақ заттың массасы үнемі өзгеріссіз қалады. Осы есеп жағдайында ол
.
Екінші жағынан
;
,
.
Ерітіндегі
-заттың
қоюлығы
деп сол зат массасының бүкіл ерітінді
массасына қатынасын айтамыз,яғни
немесе
,
-көлем.
Мұндағы
.
Қоюлық
көбінесе процентпен беріледі:
.
7-мысал:
Ыдыста
тұз
қышқылы бар еді. Қышқылдың бір бөлігін
төгіп, оның орнын сумен толтырды. Бұдан
соң бұрынғы төгілгендей мөлшерде қоспаны
тағы төгіп оны сумен толтырды. Егер
ыдыста
-тік
қышқыл ерітіндісі қалған болса, онда
қанша литр сұйық төгілген?
Шешуі:
Әр
ретте
сұйық
төгілген.Бірінші рет төгілгеннен кейін
ыдыста
ері
-тінді қалған, ондағы қышқыл мөлшері
,
мұның қоюлығы
.
Екінші рет төгілгеннен кейін ыдыста
ерітінді
қалған, ондағы қышқыл
Жаңа
қоюлығы
бұл
арадан
;
бұдан
.
Екі
ерітіндіні (не екі қоспаны) араластыратын
есептерде олардың массалары
,
,
бұларға сәйкес қоюлықтар
болса, онда мынадай схема құру қолайлы:
+ =
Бұл
арадағы
-ерітіндісінің
массалары. Бұл арадағы параметрлер
;
,
қатынастарына тәуелді. Бұл теңдіктерде
массалар орнына оларға сәйкес көлемдерді
қоюға да болады.
8-мысал:
-тік
тұз ерітіндісіне
су
қосты. Бұдан шыққан жаңа ерітіндідегі
тұздың жаңа проценттік мөлшерін табыңдар.
Шешуі:
+ =
9-мысал:
тұз ерітіндісіндегі су мөлшері
.
Ерітіндідегі су мөлшері
болу үшін қанша суды құрғату керек?
Шешуі:
+ =
.
10-мысал:
Құрамында
және
мыс бар екі қоспадан құрамында мысы
болатындай массасы
қоспа
дайындау керек. Бұл үшін
-тік
қоспадан қан -ша килограмм алу керек?
Шешуі:
+ =
,
бұлардан
жүйе құрсақ,
,
11-мысал:
Белгілі мөлшерде
-тік тз ерітідісіне
-тік
тұз ерітіндісін қосып араластырған,
соның нәтижесінде
-тік
тұз ерітіндісі алынды.
-тік
ерітндіден қанша алынды?
Шешуі:
+ =
,
,
;
;
12-мысал:
Бір қоспада алтын мен күміс мөлшері
ал екіншісінде
қатынас -ындай. Бұларды қосып алтыны
,күмісі
бөлік
болатындай екінші қоспамен ара-
ластырғанда
жаңа
қоспа алу үшін бірінші қоспадан қанша
грамм алу қажет?
Шешуі:
+ =
Б
ұлардан
жүйе құрсақ,
,
бұдан
.
