4.1. Есептер шешудегі анализ бен синтез.

Математикалық есептер шешуде анализ бен синтез кең түрде қолданылады. Анализ – ізделіндіден берілгенге қарай көше отырып талқылау жолы. Синтез – берілгеннен бастап ізделіндіге көшу (өту) жолы. Бұл екі әдісте бір-бірімен тығыз байланыста болады.

Дәлелдеуге берілген есептерді шешудегі анализ бен синтез.

1-есеп. Шар үшбұрышты пирамиданың барлық бүйір жақтарын олардың биссектрисаларының қиылысу нүктесінде жанайды. Дұрыс пирамида екенін дәлелдеңдер.

Анализ. Пирамиданың дұрыс екенін дәлелдеу үшін оның табаны дұрыс үшбұрыш екенін көрсету қажет. (АВС). Ал бүйір жақтары тең бүйірлі тең үшбұрыштар болуы керек. Бірінші сөйлемді дәлелдеу үшін АС=AB=BC көрсету керек, бұл өз кезінде АВС=АSВ=ВSС болуы қажетті. Бұл қатыстарды дәлелдеу үшін үшбұрыштың теңдік белгілерін пайдаланамыз. (пирамиданың бүйір қабырғалары). (Пирамиданың қабырғалары және оған іргелес жатқан екі бұрышы бойынша).

Шар бұл бүйір жақтарды жанау үшін O₁SC=O₂SC және O₂BS=O₃BS. (шеңбердің бір нүктесіне жүргізілген жанаманың кесінділері).

O₁S=O₂S=O₃S, O₁C=O₂C, O₂B=O₃B (бір нүктеден жүргізілген жанамалар).

2. Анализ орындалуы. Егер келесі әрбір сөйлемнің жеткіліктілігін тағайындай алсақ, онда дәлелдеу орынды деуге болады.

Синтез. O_1, O₂ нүктелері АSВ және SВС –на сәйкес биссектрисалардың қиылысу нүктелері.

(SDE) жазықтығы берілген шармен белгілі бір дөңгелек бойынша қиылысады. Дәл осы сияқты (СО₁О₂) жазықтығы берілген шарды басқа дөңгелек бойымен қиылысады.

O1S=O2S, O1C=O2C SO1C=SO2C O1SC= O2SC, O1CS= O2CS ^ACS=2^O1SC1, ^ACS=2^O1CS, ^BSC=2^O2SC, ^BCS=2^O2CS, сондықтан ASC=BSC2, және ACS=BCS. АCS=ВCS. 5-ге сүйеніп АС=BC, AS=BS.

Бір ортақ нүктеден шеңберге жүргізілген жанама кесінділері тең болады. Үш қабырғасы бойынша тең , SC-бұл -ға ортақ қабырға. Тең қабырғаларға қарсы жатқан бұрыштар тең. 3-қатыс бойынша О1S=O2S, О1C=O2C- ASC, BSC, ACS, BCS-бұрыштарына сәйкес биссектрисалар. SC қабырғасы бойынша және мұның үшбұрышындағы бұрыштар бойынша Тең үшбұрыштың тең бұрыштарына қарсы тең қабырғалар жатады.

Дәл осыған ұқсас BSC=ASB (немесе ФЫС=ASB) деген сөйлемнен BC=AB (не AC=BC) және AS=CS (не BS=CS) теңдіктері шығады.

АС=BC=AB және ABC дұрыс үшбұрышынан теңдіктің транзитивтік қасиеті бойынша ASC=ASB=BSC, AS=BS=CS, яғни пирамиданың бүйір жақтары – (өзара тең) тең бірдей. Бүйірлі үшбұрыштар. Сонымен пирамида дұрыс.

4.2. Есептер шешудің басқа да жалпы әдістері.

Есептерді шешуде анализ бен синтез есептер шешудің барынша жалпы әдісі болып табылады. Сонымен қатар төменде қарастырылатын әдістерде жалпы әдістер болып саналады.

а) Жеткілікті түрде сынау әдісі.

Есеп шартын қанағаттандыратын барлық логикалық мүмкіндіктер және оларды таңдап алу. Егер есеп шартына сай логикалық мүмкіндіктер шектеулі сандар болса, онда есеп шартына толық сай келетін әдісті сұрыптап алу. Осы әдіспен кейбір сандар теориясының есептері шешіледі.

1-мысал. Цифрларының қосындысы 11, өзі 11-ге бөлінетін барлық төрт таңбалы сандарды табыңдар.

Шешуі. Ізделінетін сан fbcd=10³a+10²b+10c+d болсын. Есеп шартына сүйеніп жүйені жазуға болады.

Осы жүйенің екінші теңдеуі ізделетін санның параллельге бөлінетінін білдіреді.

Бір-біріне қоссақ 2(а-с)=11(k+1). Мұндағы k(-1;0;1) болады. Шынында да жүйенің екінші теңдеуінде сол жағының айырмасы 11-ден кіші, 11 - деп үлкен болмауы керек.

б) Екінші әдіс. – мәліметтер әдісі.

Есептер біртіндеп түрлендіріледі. Түрлендірулер тізбегінің соңында қажетті жауапты алуға мүмкіндік береді. Егер теңдеуді шешу керек болса, онда берілген теңдеуге эквивалентті теңдеулер тізбегін құрамыз, соңғы теңдеу шешуге жеңіл, сұраған жауапты береді. Теңдеулер жүйесін, теңсіздіктер жүйесін, шешкенде де дәл осылай істейді. Дәлелдеуге берілген есептерді шешкенде де теңбе-тең түрлендірулер тізбегін жасап түсінікті теңбе-теңдікке келеміз.

2-мысал. х²-2ху+у²-2х+3>0.

Шешуі. х²-2ху+у²-2х+3=х²-2х(у+1)+(у+1)²-(у+1)²+2у²+3=(x-y-1)²+y²-2y+1+1=(x-y-1)²+(y-1)²+1>0.

Мәліметтерді қабылдаудың негізіне геометриялық салу есептерін шешу жатады. Осы түрдегі әрбір есеп мынадый талаптардан тұрады: берілген фигура арқылы, оның конструктивті элементтері арқылы фигура салады, ол есеп шартын қанағаттандыруы керек. Салынуға тиісті есеп элементар салуларға келеді. Мәліметтер әдісімен мәтіндік есептер арифметикалық тәсілмен шешіледі. Бұл арада да берілген есеп жай есепке келтіріледі.

в) Есептер шешудің үшінші әдісі: модельдеуге негізделеді.

Модельдеуге әртүрлі математикалық объектілер пайдаланылады. Сан формулалар, сан таблицалары, әріпті формулалар, функциялар, алгебралық теңдеулер, дифференциалды теңдеулер мен олардың жүйелері, теңсіздіктер, теңсіздіктер жүйесі, қатарлар, геометриялық фигуралар, әр алуан граф, схемалар, Венн диаграммалары, т.б. Математикалық модельдеу көптеген мәтіндік есептер шешуде қолданылады. Есеп шарты бойынша құрылған теңдеу – алгебралық (аналитикалық) модель болып табылады.

Берілген геометриялық есептегі фигураның сызбасы – ондағы берілгендер мен ізделетін айнымалылар да – геометриялық модель болады. Көлемді геометриялық фигура – есепте берілген заттарды кескіндеу не оны қолдану моделі болады.

3-мысал. Егер сыныптағы оқушыға 2-ден конфет таратылса, онда 17 конфет артылады. Егер 3 конфеттен таратылса, онда 2 оқушыға конфет жетпейді. Сыныпта неше оқушы, неше конфет?

Бұл есепті 2 сызықтық теңдеу құру арқылы шешуге болады. Егер бұған модуль құрсақ, онда бұл есепті бастауыш сынып оқушылары шеше алады.

2 2 2 ... 2 22+17

   ...  

3 3 3 ... 3

Модельден байқалатындай: 2 конфет алған оқушы 3 конфет алуы үшін 17 конфетті және 4 конфетті тарату керек. Өйткені 2 оқушыға конфет жетпей қалған. Яғни қосымша 21 конфет тарату керек. Демек, сыныпта 23 оқушы. А, конфет 21 3=63.

Орта мекетеп математикасында графиктік модельдеу ерекше роль атқарады: диаграммалар, функциялық графигі, теңдеудің, теңсіздіктің, графиктің геометриялық мағынасы.

4-мысал. Екіншілер бригадасы бірі екіншісінен 2 еседен көбірек шабындықты шабу керек. Олар жарты күнде үлкен шабындықта болды. Түстен кейін бригаданың жартысы үлкен шабындықта қалды да кешке дейін оны ақырына дейін шауып бітірді. Бригаданың екінші жартысы түстен кейін кіші шабындықта болды. Олар толық шауып бітіре алмады. Шабылмай қалған жерді келесі күні 1 шалғышы шауып бітірді. Бригадада неше шалғышы бар? Барлық шалғышылардың бір күнде шабатын жер мөлшері бірдей.

Ш ешуі. Шалғышылар саны – х; 0,5x

Е сеп шарты диаграммада көрсетілген.

0,5х+2=0,5 1,5x x 0,5x

x=8

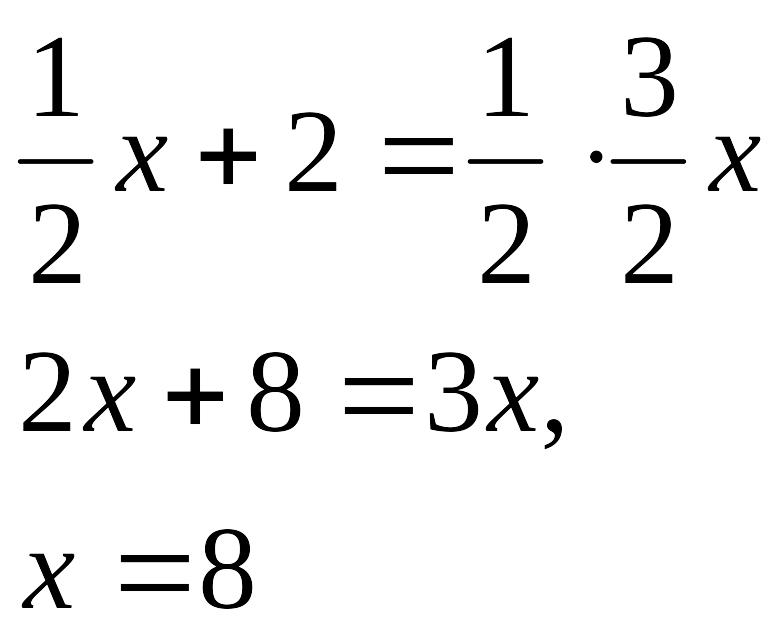
г) Ізделетін шаманың мәнін біртіндеп жуықтап есептеу әдісі.

Есептерді графиктік тәсілмен шешудің бәрі жуық түрде есептеледі. Жуықтап шешу сандар әдісі (мысалы, квадрат теңдеудің түбірлерінің шешімі формула бойынша табылады).

Геометрияда жуықтап салу методы бар.

Мысалы, дөңгелекке тең квадрат салу бұрышты тең бөліктерге бөлу, т.б. Практикалық мазмұнды есептер көбінесе комбициялық әдістермен шешіледі. Орта мектепте есептер шешудің негізгі мақсаттарының бірі - әр оқушының математикалық есептердің негізгі методтар мен есеп шешудің тәсілдерін меңгеруін қамтамасыз ету.

Теңдеулерді шешу

3-мысал: теңдеуін шешіңдер.

Шешуі: десек,

4-мысал: теңдеуінің түбірлері шартын қанағаттандырады. -ны табыңдар.

Шешуі: теңдеуін түрлендірсек, . Виет теоремасы бойынша бұларды соңғы теңдеуге қойсақ .

5-мысал: -нің қандай мәнінде теңдеуінің түбірлерінің айырмасы түбірлерінің көбейтіндісіне тең болады?

Шешуі: Егер - берілген теңдеудің түбірлері болса, онда есеп шарты бойын -ша осы теңдіктің екі жағын квадраттасақ,

Виет теоремасы бойынша соңғы теңдеу

не осыдан

6-мысал: Түбірлері , болатын квадрат теңдеу құрыңдар.

Шешуі: Ізделінді теңдеу түрінде болады.

, осы мәндерді теңдеуіндегі орнына қойсақ, не

3-мысал: теңдеуін шешу керек.

Шешуі: Анықталу аймағы . Бұл жағдайда ( және ). Сонымен, анықталу аймағы .

Берілген теңдеудің екі жағын квадраттасақ, , бұдан екінші рет квадраттасақ, бұдан

. -анықталу аймағына тиісті емес. Жауабы: .

4-мысал: теңдеудің түбірлерінің қосындысын табыңдар.

Шешуі: Берілген теңдеуден бұдан

,

Теңдеулерден , -бұл мән анықталу аймағына ен -бейді, демек, түбір емес.

Екінші теңдеуден , бұдан бұ -лардың екеуі де анықталу аймағына тиісті, екеуіне .

6-мысал: теңдеуін шешу керек.

Шешуі: , ,

7-мысал: теңдеуін шешу керек.

Шешуі: болғандықтан теңдеудің екі жағын өрнегіне бөліп, берілген- ге мәндес немесе

бұл арадан , .

8-мысал: тңдеуін шешу керек.

Шешуі: Берілген теңдеуді көбейтіштерге жіктейміз.

.

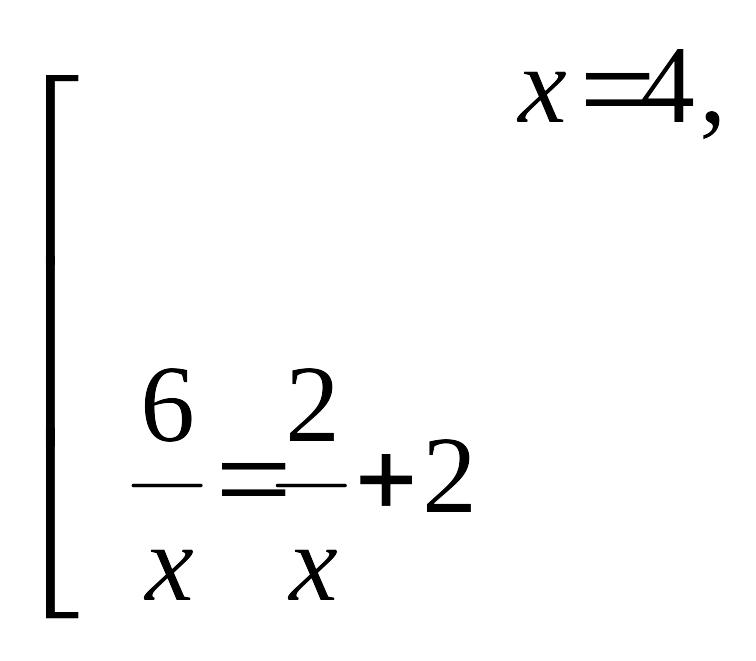
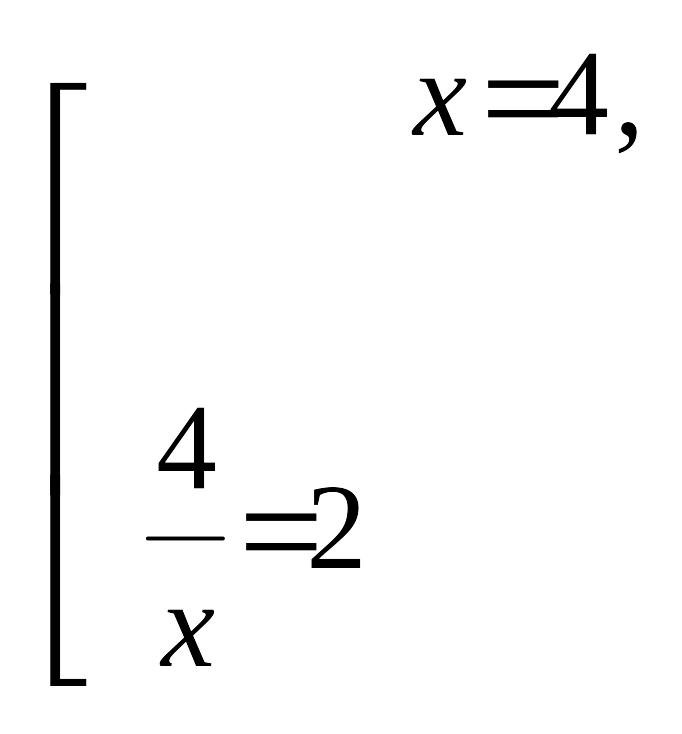
Айнымалысы түбір таңбасына тәуелді теңдеулер

Модуль таңбасына тәуелді ең қарапайым теңдеу (1) түрде болады. Мұндағы -нақты айнымалының функциясы, -нақты сан. болса ғана теңдеу- дің түбірі болады (өйткені ).

Егер болса, онда ;

Егер болса, онда , .

(2) күрделі түрде берілуі мүмкін. десек, онда (3).

(3) теңдеудің оң түбірлері болса ғана, (2) теңдеудің түбірін табу үшін ,

, .... түріндегі теңдеулер жиынтығын шешеді. (4) түрін- дегі теңдеулерде болады, мұндағы функциясы және -ке тәуелдіб ол (5) теңдеулер жиынтығымен мәндес.

Айнымалысы модуль таңбасына тәуелді теңдеулерді өзара қиылыспайтын жи - ындарда модултдерді «ашу» арқылы шешеді. Бұл әдістің мәні мынада: 1) модулі нөлге тең болатын айнымалының мәнін табады; 2) теңдеудің анықталу аймағын ұштарында модульдер нөлге тең болатын аралықтарға бөледі;3)Бөлінген әрбір аралықта, модульде тұрған өрнектің таңбасын анықтайды; 4) Әрбір аралықта мо- дульді ашып, теңдеуді шешеді;5) табылған түбір қарастырылған аралықта жата ма соны тексереді. Егер табылған түбір сол аралықта жатса, онда оны есептің жауабы үшін алады, егер табылған түбір сол аралықта жатпаса, онда оны қалдырады.

Аталған әдіспен (6) .... , сияқты теңдеу- лер шешіледі - нақты сандар, -айнымалы, - берілген функциялар.

1-мысал: теңдеуін шешу керек.

Шешуі: Берілген теңдеу , теңдеулерімен мәндес. Бірінші – сінен Екіншісінде болғандықтан нақты түбірі болмай- ды.

2-мысал: теңдеуін шешейік.

Шешуі: Берілген теңдеу және теңдеулерімен мәндес.

Біріншісінен ,

Екіншісінен .

3-мысал: теңдеуін шешу керек.

Шешуі: Теңдеудің анықталу аймағы тек оң сандар жиыны, яғни функция - лардың нөлдерін табайық. бұлардан - бұл сандар сан аралығын үш аралыққа бөледі:

болғандықтан аралықтары ғана қарастырылады.

1) -да , , -да сондықтан теңдеуге түбір.

Енді , бұдан сондықтан түбір емес.

4-мысал: теңдеуін шешу керек.

Шешуі: Теңдеуді ықшамдасақ, шығады. Бұдан , -модульдің түбірі, сан аралығын , екі аралыққа бөледі. болғандықтан қарастырылатын аралықтар болып өзгереді. Егер

-да жатса, онда бұдан Ал, -да

бұдан Сонымен, теңдеудің деген екі шешімі бар.

5-мысал: теңдеуін шешу керек.

Шешуі: Модульдің нөлдері , берілген аралығын

аралықтарына бөледі. Егер болса, онда берілген теңдеу . Егер жатса, берілген теңдеу онда Бұл жағдайда аралығы теңдеуді толық қанағаттандырады. болғанда Егер онда бұдан бұл жағдайда теңдеудің шешімі жоқ. Со- нымен теңдеудің шешімі .

6-мысал: теңдеуінің түбірлерінің көбейтіндісін табыңдар.

Шешуі: Алдымен модуль таңбасына тәуелді функцияның нөлдерін табамыз:

бұлардан Бұл сандар сан осін

аралықтарына бөледі.

1) болғанда

-да ендеше теңдеуге түбір болады.

2) болса, онда берілген теңдеу , ,

сондықтан бұл мән теңдеуге түбір.

3) -да берілген теңдеу, сон -дықтан теңдеуге түбір бола алмайды.

4) -да берілген теңдеу, , -бұл мән

да жатпайды. Сонымен теңдеудің екі түбір бар, бұлардың көбей- тіндісі

7-мысал: теңдеуін шешу керек.

Шешуі: Берілген теңдеудің сол жағы теріс емес, олай болса, оң жағы Демек, дегенді білдіреді, сондықтан Бұл жағдайда беріл -ген теңдеу

Бұл арадан

Алгебралық теңдеулермен теңсіздік жүйесіне келтірілетін есептер

1-мысал: Екі таңбалы санның цифрларының қосындысы .Егер ізделінді саннан

-ды азайтса, онда одан шығатын айырмадағы цифрлар ізделінді сандағы цифр -лардың орындары ауысып жазылған сан шығады. Ізделінді санды табыңдар.

Шешуі: Ізделінді екі таңбалы санның ондық цифрын , бірлігін әрпімен белгі- лесек, онда ізделінді сан ал -цифрларының орындары ауысқан сан. Есеп шартынан немесе

Соңғы жүйені шешсек, ізделінді сан

2-мысал: Кітапханада ағылшын, француз, неміс тіліндегі кітаптар бар. Ағылшын тіліндегі кітаптар барлық шет тіліндегі кітаптардың -і, ал француз тіліндегісі ағылшын тіліндегі кітаптардың -і. Қалған кітап неміс тіліндегі кітаптар. Кітапханада шет тілінде барлығы қанша кітап бар?

Шешуі: Барлық шет тіліндегі кітаптар санын десек, -ағылшын тілінде, -француз тілінде, -неміс тіліндегі кітаптар.

Демек, осы теңдіктен

не

, кітап.

3-мысал: Завод қаңтарда өзінің айлық тапсырмасын -ке орындады, ал ақпан- да қаңтардағыдан көп орындады. Завод екі айлық жоспарын неше процентке артық орындады?

Шешуі: Заводтың бір айда орындайтын тапсырмасының мөлшері болсын. Бұл жағдайда қаңтарда ақпанда екі айда жоспар- да екі айда орындағаны .Бұл неше процентті құрайды?

Демек, завод екі айлық жоспарын -ке артық орындады.

4-мысал: Саяхатшы екі қаланың арасын күнде жүріп өтті. Бірінші күні барлық жолдың бөлігін және екінші күні барлық жолдың -і және , үшінші күні барлық жолдың бөлігін және қалған жолды жүрді. Екі қаланың ара- сы қанша километр?

Шешуі: Екі қаланың арасы болсын. Онда есеп шарты бойынша бірінші күні екінші күні үшінші күні жүрді. Үш күнде барлық

жолды жүргендіктен

5-мысал: Мыс пен мырыштың қоспасында мыс бар. -тік мысы бар жаңа қоспа алу үшін осы қоспаға қанша таза мыс қосу керек? қоспада мыс мөлшері яғни мыс бар. Қоспаға қосылатын мыс мөлшерін десек, жаңа қоспадағы мыс мөлшері осы қоспадағы мыс, Жаңа қоспадағы мыс болуы керек еді, ендеше бұдан

6-мысал: Бір су құбырында екіншісінде су бар. Егер шүмектерді аш- ып қойғаннан кейін құбырлар неше сағаттан соң толады? Егер екінші құбырға са -ғат сайын су артық құйылатын болса, онда неше сағаттан соң екі құбырдағы су мөлшері бірдей болады?

Шешуі: Бірінші құбырдың толтыру жылдамдығы ,екіншісінікі .

Егер шүмектер сағат ашық тұрса, онда бірінші бассейінде , екінші –сінде су болады. Бұл су мөлшері бірдей. Демек,

бұдан сағат өткенде екі құбырдағы су мөлшері бірдей болады.

7-мысал: Электропоезд қаласынан шығып өзінің жүруге тиісті жолының -ін

яғни жүргеннен соң жолда жарты сағат кідіріп қалды. Кешікпеу үшін жүргі- зуші жылдамдығын -қа арттырып, қаласына өз уағында келді. Поездің бастапқы жылдамдығын табу керек.

Шешуі: Поездің бастапқы жылдамдығы , онда соңғы жылдамдық . Есеп шартына сүйеніп уақыт бойынша теңдеу құрсақ,

бұдан бұдан

8-мысал: Бір бригада егістікті күнде, екіншісі осы жұмысты аталған уақыттың -де орындай алады. Бірінші бригада жеке өзі күн егісті жинаған соң оған екінші бригада келіп қосылды. Екеуі бірлесіп жұмысты аяқтады. Екі бригада жұ -мысты қанша күн бірге істеді?

Шешуі: Бүкіл жұмысты бүтін есептесек, онда бірінші бригаданың жұмыс өнім –ділігі екінші бригада жұмысты жеке орындауына күн қажет, оның жұ -мыс өнімділігі . Бірінші бригада күнде жұмыстың бөлігін орындайды. Қал- ған -күнде екі бригада жұмыстың бөлігін орындайды. Ендеше есеп шар- ты бойынша теңдеуін жаза аламыз. Осы теңдеуді шешсек, . Демек, екі бригада бірлесіп күн жұмыс істейді.

9-мысал: Магазинге сату үшін физика және математика оқулықтары түсті. Мате –матика оқулығының -і физика оқулығының сатылғаннан соң барлығы оқулық сатылды.Және физика оқулығына қарағанда математика есе көп қал- ғаны белгілі болды. Магазинге әрқайсы оқулықтан қанша түскен?

Шешуі: Магазинге математика оқулығы, физика оқулығы сату үшін қойылды дейік. Бірінші рет оқулық сатылды. Мұның -і математика, -і физика болғандықтан математикадан физикадан кітап сатылған. Олай болса, теңдігін жазуға болады. Есеп шарты бойынша Бұлардан жүйе құрсақ, Демек, математика оқулығы,

оқулығы сатуға шығарылған.

10-мысал: Спорт мектебінің үш секциясында спортшы бар. Мұзда сырғанаушы спортшылар саны шаңғы тебушілердің бөлігін құрайды.Ал,хоккейшілер алғаш- қы екі секциядағы спортшылардың -ін құрайды.Әр секцияда қанша спортшы-

дан бар?

Шешуі: -мұзда сырғанушылар, -шаңғы тебушілер, -хоккейшілер саны болсын.

Есеп шарты бойынша хоккейшілер алғашқы екі секцияның үштен біріндей

яғни Соңғы жүйені шешсек,

Демек,

11-мысал: Жаяу мен велосипедші арақашықтығы . мен орындарынан кез- десу үшін бір мезгілде жолға шықты. Жолға шыққаннан кейін сағат өткенде олар кездесті. Олар өз бағыттарымен одан әрі жүрді.Жаяудың -ға келуінен вело- сипедші сағат бұрын -ға келді. Егер олар жолда тұрақты жылдамдықпен қозғалса, онда велосипедші мен жаяудың жылдамдықтарын табыңдар.

Шешуі: -жаяудың, -велосипедшінің жылдамдығы болсын. са -ғат өткенде кездесетіндіктен Жаяу жолда сағат, вело-

сипедші сағат болды. Жаяуға қарағанда велосипедшінің уақыты сағат аз. Сондықтан , бұл теңдеудің түбірлері және Жаяу жылдамдықпен жүре алмайды. Жаяу , ал велосипедші

жылдамдықпен жүрген.

12-мысал: Әрқайсысындағы мыс мөлшері әртүрлі екі қоспа бар. Бірінші қоспада- ғы мыстың мыстың мөлшерін процентпен анықтайтын сан екінші қоспадағы мыс мөлшерін процентпен өлшейтін саннан -қа кем. Бұл екі қоспаны қосып қорыт-қанда шыққан қоспадағы мыс мөлшері болды. Егер бірінші қоспада , екін- шісінде мыс болса, онда әр қоспадағы мыстың проценттік мөлшерін анықтаң- дар.

Шешуі: Бірінші қоспада мыс, екіншісінде мыс бар екен дейік. Бірінші қоспаның массасы , екіншісінікі болсын. Бірінші қоспадағы мыстың мөлшері болғандықтан

Дәл осы сияқты екінші қоспада мыс болғандықтан Екі қоспаны қорытқаннан соң масса шығады, бұларда

мыс бар. Жаңа қоспадағы мыстың мөлшері , олай болса, бұдан шығады. екенін ескерсек, Бірінші қоспадағы мыс мөлшері , екіншісінде .

Көрсеткіштік теңдеулер жүйесі

Көрсеткіштік теңдеулер жүйесін шешкенде орнына қою әдісі, айнымалыны ауыстыру әдісі, теңдеудің екі бөлігін ауыстыру т.б. әдістер қолданылады.

1-мысал: 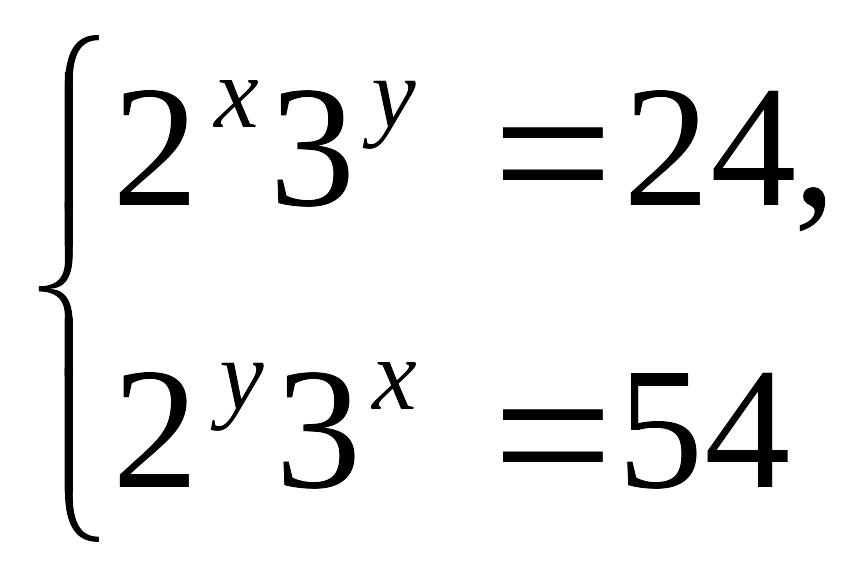теңдеулер жүйесін шешу керек.

Шешуі: Берілген жүйе теңдеулерін өзара көбейтсек, .

(1).

Енді берілген теңдеуді бір-біріне бөлсек, немесе не бұдан (2). (1) мен (2) теңдеулерден бұдан

2-мысал: теңдеулер жүйесін шешу керек.

Шешуі: деп белгілесек, осы жүйені орнына қою әдісі бо- йынша шешсек, мұны жүйенің екінші теңдеуіне қойсақ,

не бұлардан -ды тапсақ,

Сонымен, белгілеуге қайта оралсақ,

теңдеуінің шешімі жоқ.

Жауабы:

3-мысал: теңдеулер жүйесін шешу керек.

Шешуі: Жүйенің бірінші теңдеуін деп, екі жағын квадраттасақ,

Енді деп белгілесек, бұлардан сондықтан

Берілген жүйенің шешімі

4-мысал: 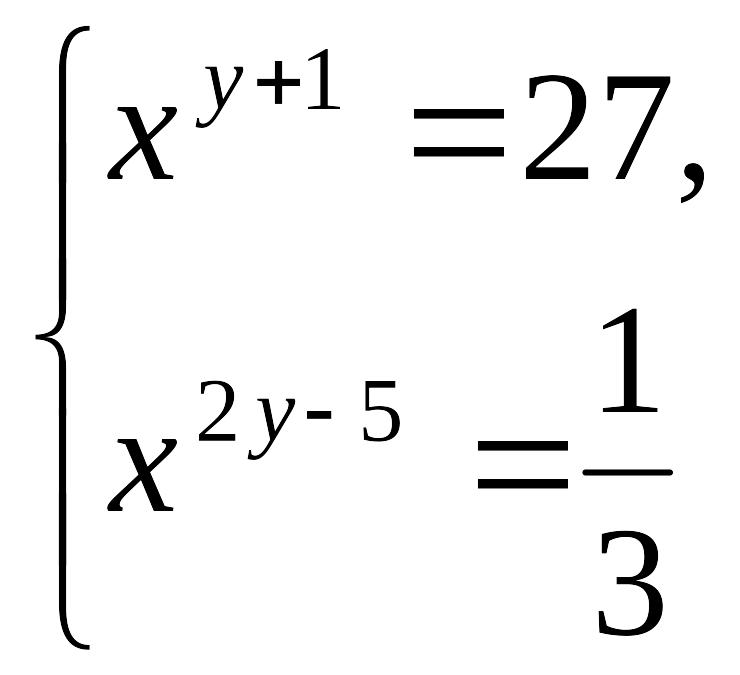теңдеулер жүйесін шешу керек.

Шешуі: теңдеулердің екі жағын негізінде логарифмдейміз: жүйе-нің бірінші теңдеуін екіншіге бөлсек,

-тің мәнін бірінші теңдеудегі орнына қойсақ, Жүйенің жалғыз шешімі бар:

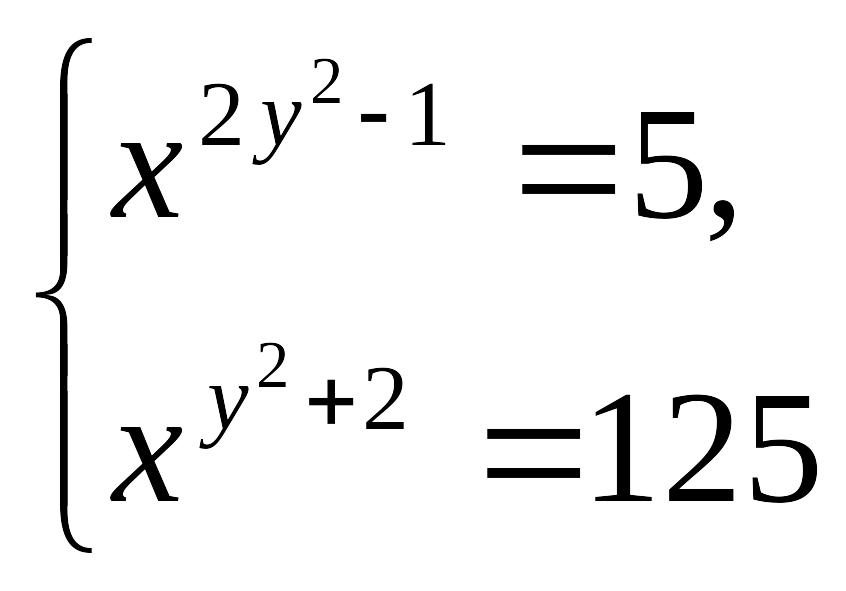5-мысал: теңдеулер жүйесін шешу керек.

Шешуі: Жүйенің екінші теңдеуін біріншісіне бөлсек Енді бірінші тең –деуді квадраттасақ, бұлардан теңдігін жаза аламыз. Соңғы

теңдеуден

Енді теңдеуінен -ті табамыз.

Сонымен, жүйенің шешімі

Логарифмдік теңдеулер жүйесі

Логарифмдік теңдеулер жүйесін шешу үшін логарифмдеу ережесі, потенцирлеу, айнымалыны ауыстыру т.б. әдістер қолданылады.

1-мысал: теңдеулер жүйесін шешу керек.

Шешуі: Жүйенің бірінші теңдеуінен мұны екінші теңдеуге қойсақ не

,

Анықталу облысы бойынша олай болса,

2-мысал: жүйесін шешу керек.

Шешуі: Жүйенің бірінші теңдеуінен бұдан мұны жүйенің екінші теңдеуімен бірге қарастырамыз: ,

бұдан Ал, болғандықтан

Жауабы

3-мысал:

теңдеулер жүйесін шешу керек.

Шешуі: Логарифмнің қасиеті бойынша жазсақ, 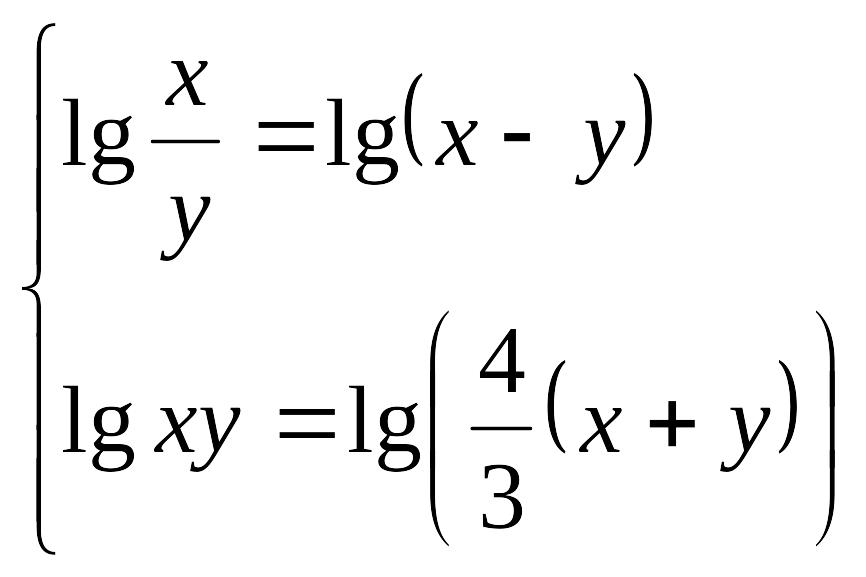потенцирлесек,

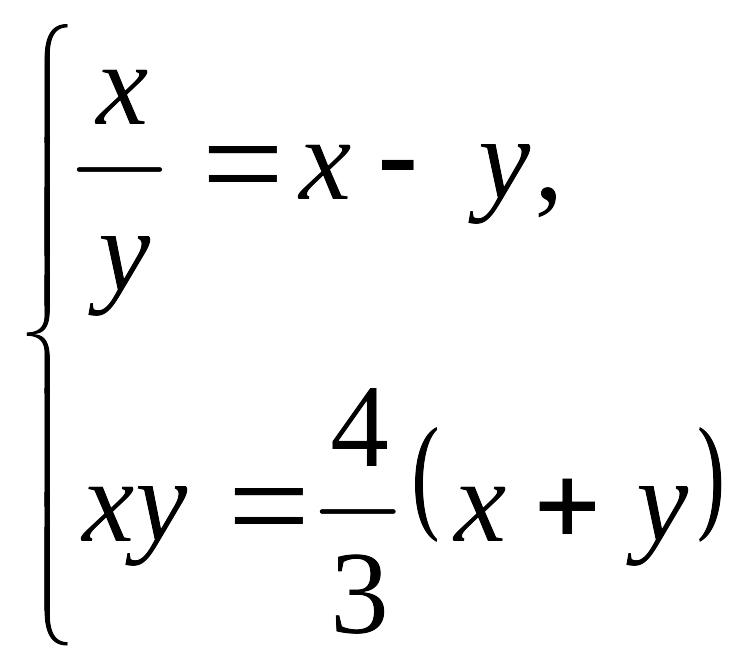, болатынын ескереміз. Осы жүйеден , .

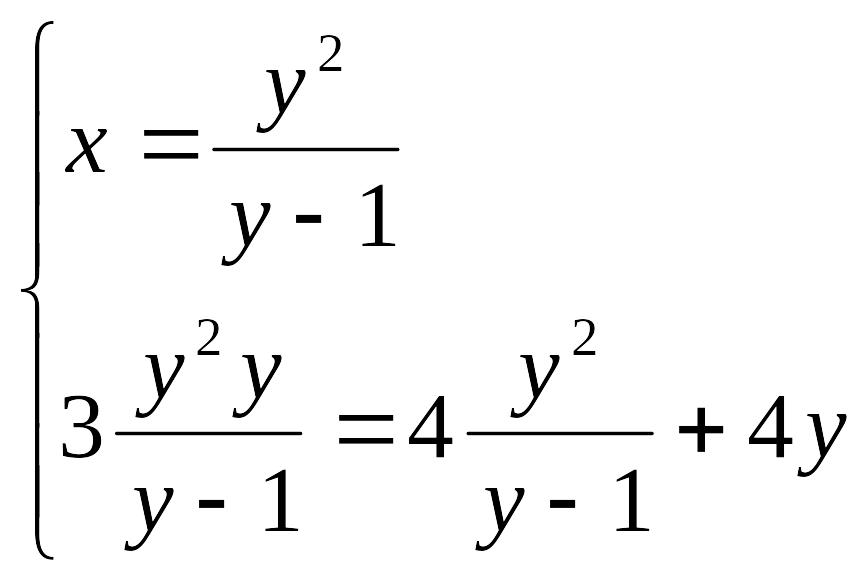бұдан Бұдан болуы керек.

Жауабы:

4-мысал: , теңдеулер жүйесін шешу керек.

Шешуі: Логарифмнің формуласы бойынша бұдан мұны жүйенің екінші теңдеуіне қойсақ, болғандықтан

4-мысал.

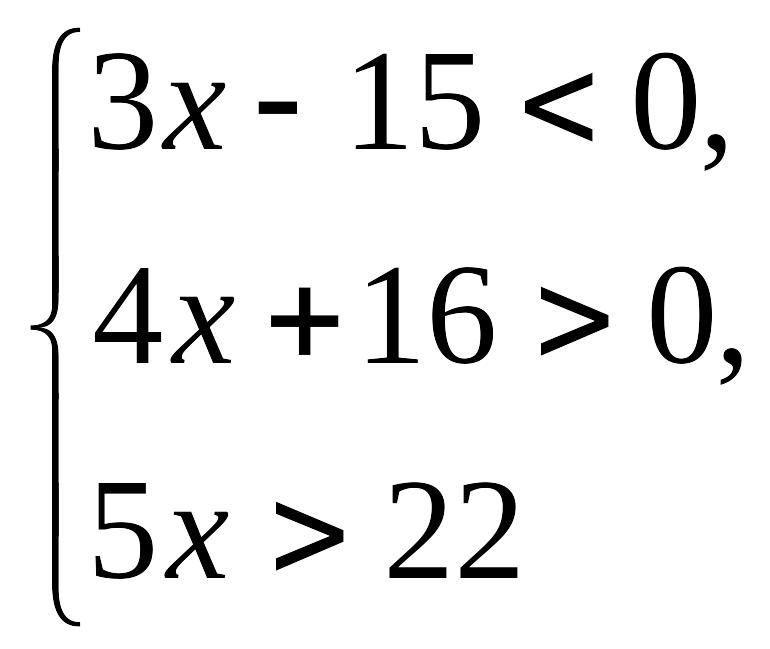теңсіздіктер жүйесін шешу керек.

Шешуі: Берілген жүйе

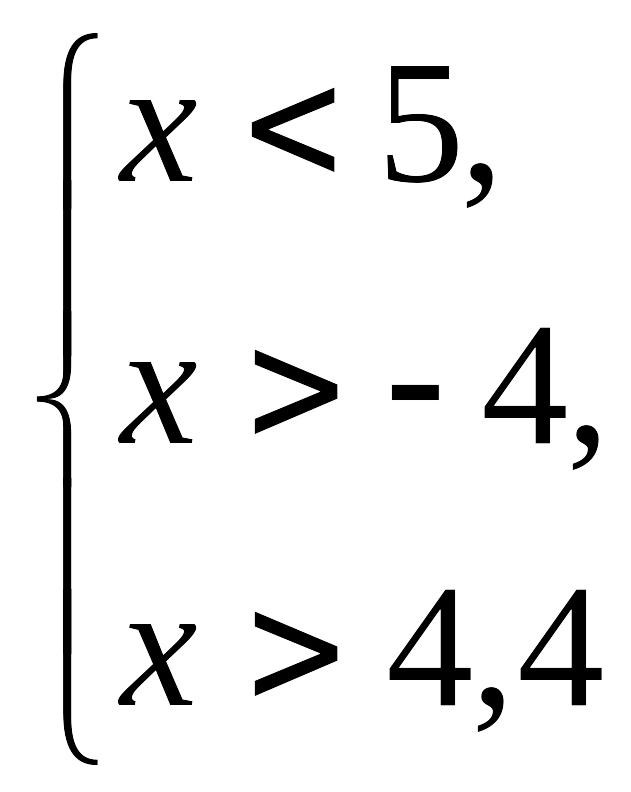алғашқы екі теңсіздіктен және болғандықтан жалпы алғанда

5-мысал. қос теңсіздігін шешу керек.

Шешуі: Теңсіздіктің әр бөлігіне (-3)-ті қосамыз, сонда , соңғы теңсіздіктің әр бөлігін (-4)-ке бөлсек,

6-мысал. теңсіздігін шешу керек.

Шешуі: Берілген теңсіздікті ортақ бөлімге келтірсек,

не

сандары аралығын аралықтарына бөледі.

көбейтіндісі және болғанда оң болады. Сонымен, теңсіздіктің шешімі және аралықтары.