2. Мектепте теңдеулер құру арқылы геометриялық есептерді шешудің оқушылырдың математикалық ойлауы мен пәнге қызығушылығын дамытудағы рөлі

Қазіргі заман мектеп геометриясын оқыту үрдісінде есептерді түрлі әдіс тәсілдермен шығару сонын ішінде геометриялық есептерді алгебралық, тригонометриялық теңдеулер арқылы шығару жолдары қосу мәселесі болашақ мұғалімдердің кәсіби шеберліктерін шыңдаудың көкейкесті мәселелерінің бірі болып табылады. Оқулықтармен геометриялық есептердің шығарылу методтарын, қызықты есептер, әдеби кітаптар, сөздіктер, дидактикалық, энциклопедиялық материалдар, зерттеулердің нәтижелері, жаңа ақпарат құралдары, инновациялық технологиялар, компьютерлік анимациялар, оргами т.б. қосымша материалдарды сабақ үрдісінде пайдалану қазіргі заман сабағының дәстүрлік сабақтан айырмашылықтарының бірі болып табылады. Көптеген классикалық, олимпиядалық, қызықты есептер білім алушылардың логикалық ойлау қабілетін дамытумен қатар, олардың математикалық сөйлемдерді оңай түсінуіне, кеңістіктегі фигураларды елестете алуына жағдай жасайды және оларды қиын ситуацияларда дұрыс шешім қабылдауға үйретеді, математиканы табиғатпен байланыстырады.

Оқушыларды есеп шығаруға үйрету мәселесі ертеден келе жатыр. Есеп шығара білу – оқу материалын игеру мен математикалық дамудың негізгі көрсеткіштерінің бірі. Оның жаңа аспекттерінің бәрі жоғарыда көрсетілген бағыттардың шешімін таппауына байланысты болады. Математиканы мектепте тереңдетіп оқытуда оқушылардың есептерге оқыту, конструкциялау және зерттеу объектісі ретіндегі қөзқарастарын қалыптастыру қажет. Сондықтан, есептер шығарудың әртүрлі оқыту әдістемелері талап етіледі. Олардың төмендегі классификациясын келтіруге болады:

1. Нысандардың сипаттамасы бойынша (практикалық, қолданбалы);

2. Теорияға қатысты (стандарт, стандарт емес);

3. Талап ету сипаттамасы бойынша (ізделінділерді табу, дәлелдеу, салу) т.б.

3.Геометриялық стандарт емес есептер шығару жолдары

Стандарты емес есеп дегеніміз белгілі алгоритім бойынша шығарылмайтын есептерді айтуымызға болады, әр бір есептің өз жеке алгоритімді талап ететін есептерді геометриялық есептерді айтуымызға болады. Стандарт емес қызықты есептерді шығаруға дағдыландыру, - деп біз біріншіден стандарт емес ойлауға үйрететін есептерді және «идеялар банкі» болып табылатын белгілі классикалық, тарихи, көне, өлең, басқа санау жүйелерінде берілген т.б. қызықты есептерді шығаруды, екіншіден стандарт есептерді стандарт емес түрде бергенде, оқушылардың алған білімдерін тиімді пайдаланып, ол есептерді өздері стандарт түрге келтіріп, белгілі формулаларды қолдана алуға үйретуді түсінеміз.

Геометриялық стандарт емес конкурстық-есепке мысал келтірейік. Қандай да бір шеңберге сырттай сызылған төртбұрышы диагоналі арқылы және үшбұрыштарына бөлінген. Үшбұрыштарға іштей сызылған шеңберлердің радиустары сәйкесінше 1 және . және үшбұрыштарының аудандары сәйкесінше 6 және .

Төртбұрыштың қабырғалары мен диагоналінің ұзындықтарын табыңыз.

Шешуі. Алдымен, келесі тұжырымды дәлелдейік.

Айталық, ұшбұрышына іштей сызылған шеңбер оның қабырғаларын сәйкесінше нүктелерінде жанайтын болсын (1-сурет).

теңдігін дәлелдейік. Ол үшін шеңберден тыс нүктеден жүргізілген жанамалардың бөліктерінің қасиетін пайдаланып

AE = AF = x; BF = BD = y, CD = CE = z

белгілеулерін енгізе аламыз. Сонда жарты перимерт: болады. Осыдан ,

яғни: .

Дәлелдеу керегі осы.

Осыған ұқсас ; болады.

Айталық ABC және CDA үшбұрышына іштей сызылған шеңберлер төртбұрыштың AC диагоналін сәйкесінше M және K нүктелерінде жанайтын болсын (2-сурет). Жоғарыда дәлелденген теңдіктерді пайдалансақ:

, аламыз.

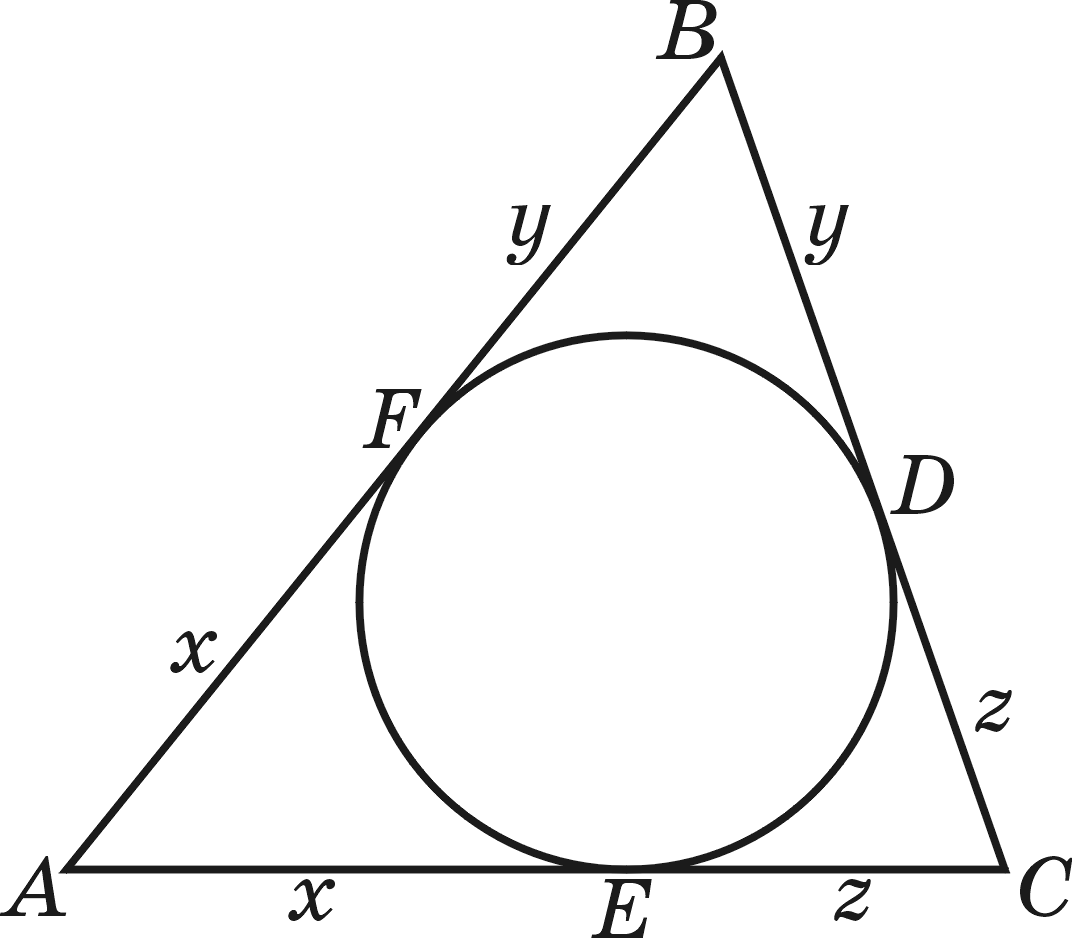
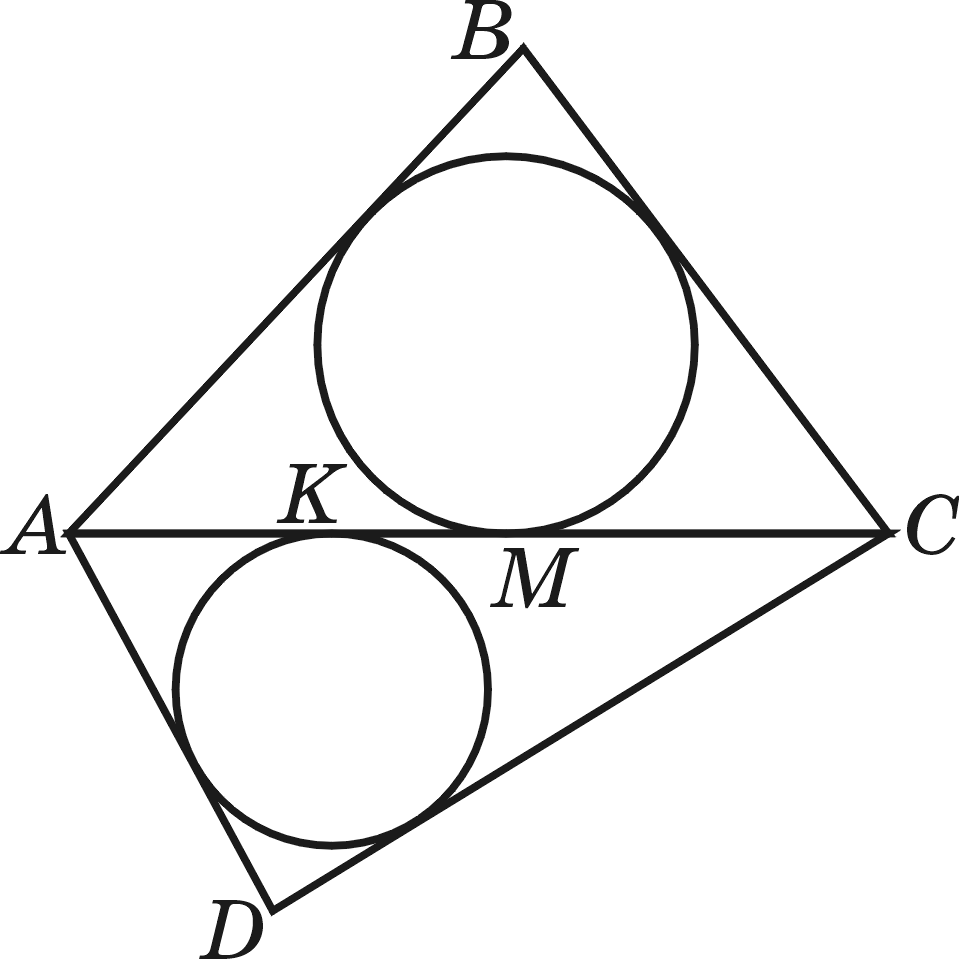
1-сурет 2-сурет

Осыдaн

.

Шарт бойынша ABCD төртбұрышы сырттай сызылған, ендеше

AB + CD = BC + AD, AM – AK = 0, осыдан AM = AK екендігі және M мен N нүктелері беттесетіні шығады (3-сурет). Енді ABC және ACD үшбұрыштарының жарты периметрлерін және , іштей сызылған шеңберлердің радиустарын сәйкесінше және , ал төртбұрыштың қабырғаларын

AB = b, BC = c, CD = d, DA = a, AC = l

деп белгілейік.

Есептің шарты бойынша , яғни және

; _{; .}

Герон формуласын пайдаланып, былай жаза аламыз:

.

Осыдан .

Осылай , . Осы теңдеулердің біріншісін екіншісіне бөлсек:

( )

шығады. Енді ABC үшбұрышынан

және ACD үшбұрышынан екенін ескерсек: немесе болады.

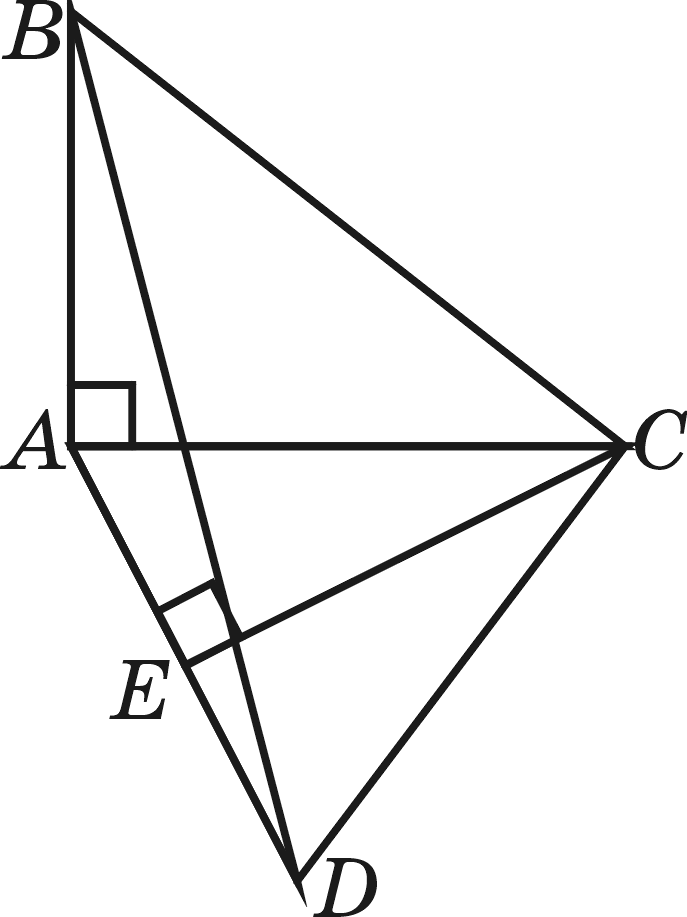
3-сурет 4-сурет

Дәл осылай, ; аламыз.

Енді d = c – 1 және b = a + 1 мәндерді ( )-ға қойсақ:

немесе 6 – l = 10 – 2l, осыдан l = 4 шығады. Сондай-ақ , осыдан , .

Табылған мәндерді теңдеуіне қойып b мен c-ның мәндерін табамыз: немесе ; ; ; Онда . Нақтылау үшін былай деп алайық: . Бұл жағдайда , . Осыдан Пифагор теоремасына кері теорема бойынша -қа тең деген қорытындыға (Мысыр үшбұрышы: ) келеміз.

Тең бүйірлі үшбұрыш ACD-ның биіктігі CE-ні (4-сурет) жүргізейік. Айталық, болсын. Онда, .

Косинустар теоремасы бойынша BAD үшбұрышынан:

немесе аламыз.

Келесі жағдайында, тік болады да, мынаны аламыз: .

Жауабы: 1) ;

2) [10-11].

Оқушылар түрлі деңгейдегі олимпиадаға қатысқанда және мектептік, қалалық олимпиадалар өткізгенде, тәжірибе көрсеткендей, геометрия есептері көп қиындықтар туғызады. Ал геометрия болса, стандартты емес ойлауды дамытып, математикамен айналысуға қабілетті адамдарды анықтайтыны белгілі. Мұндай олимпиадалық есептер кеңінен беріледі.

Бұл есептер кесуге де, құруға да, бұрыштарды табуға да арналады. Бірақ, көбінде өз шешімінде ерекше идеяны, көбінде қосымша құруды қолданатын есептер кездеседі.

Төменде сабақта қарастырып, олардың шешімдерін тақырыппен байланыстыруға болатын геометрия бойынша бірнеше олимпиадалық есепті талдап көрелік.

Мұндай есептің шешуін табу кейбір ойлау сапасы мен әдістерін қажет ететіндіктен, онда сабақта кейбір ойлау сапасын дамытуға (ең алдымен икемділікпен теренділік) сондай - ақ ойлау қызметінің әдістеріне (ең адымен талдауға ол әсіресе олимпиадалық есептерде, соның ішінде геометриялық есептерде қолданылады) көңіл бөлу керек.