1.2 Мәтінді есептердің математикалық моделін құруға қойылатын талаптар және олардың математикалық моделі.

Мектепте математикалық білім берудің маңызды проблемаларының бірі-оқушы есепті шешудің әдіс-тәсілдерімен қаруландыру және оны есептің шешімін өздігінен іздеп,таба білуге үйрету. Психологтардың,әдіскерлердің зерттеулерінде оқушының есептерді шеше білуі,ол шешкен есептер санына тәуелді емес оның есепті талдау дағдысының,есепті шешу жоспарын іздеу дағдысының дұрыс қалыптасуына байланысты екенін дәлелдеген. Бұл дағдылар қалыптаспаған жағдайда,оқушы есепті өздігінен шешуге үйренбейді.

Мәтінді есептерді шешудің оқушыларға қиындық туғызу себептері :

1.Есептің шартын дурыс талдай алмауы;

2.Шамалар арасындағы байланысты дұрыс меңгермеу;

3.Тірек- есептерді шешу дағдыларының дұрыс қалыптаспауы;

4.Есеп шығару барысында оқытушы тарапынан оқушының ойлау әрекетін жеткіліксіз басқару;

5.Есеп шығару әдістерін иеңгертуде оқытушының сабақтылық,бірізділік және жүйелік принциптерін дұрыс сақтамауы;[5, б. 11].

Мәтінді есептерді шешуде ең алдымен дайындық кезеңінің дұрыс ұйымдастырылуының маңызы өте зор.

Дайындық кезеңінде тірек-есептерді дұрыс таңдап алып,оны шешу әдістерін жүйелі қайталап отыруға көңіл бөлінуі керек.

Мәтінді есептердің ішінде ең жиі кездесетіні қозғалысқа және жұмысқа берілген есептер. Осы есептердің математикалық моделін кесте құру арқылы шешу тәсілдерін қарастырып көрейік.

Ең алдымен жұмыстың нәтижелілігін қамтамасыз ету үшін дайындық кезеңіне ерекше көңіл беру керек. Дайындық кезеңінде шамалар арасындағы байланысты көрнекілік арқылы дұрыс меңгертіп,дайын кестелер арқылы жақындау,алыстау жылдамдықтарын табуды ауызша жаттығулар құрамына енгізу және математикалық диктанттар арқылы жүйелі ұайталап отыру қажет.[6].

Мысалы: 5-9 сыныптарда қозғалысқа берілген есептерді шешуге кіріспес бұрын,әр сабақта жақындау,алыстау жылдамдықтарын табуға берілген қарапайым есептерді,жылдамдық,уақыт,жол арасындағы байланыстарға ,сол сияқты жұмысқа берілген есептерде жұмыс,уақыт,өнімділік арасындағы байланыстарға берілген есептерді,ауызша жаттығулар құрамына енгізіп және математикалық диктанттар арқылы,жүйелі түрде параллель қайталауды жүргізіп отырған жөн.

Шамалар арасындағы байланыс айқын көрінуі үшін,есеп мазмұнына сәйкес сызбаны салып көрсету, есептің шартына сәйкес кесте құру арқылы шешу,оқушының есеп шартын саналы дұрыс түсініп,есепті теңдеу құру арқылы шешу тәсілдерін саналы меңгеруіне мүмкіндік береді.

Қозғалысқа берілген есептер.

Қозғалысқа берілген есептерді шешуде оқушының мыналарды жақсы меңгеруінің маңызы зор.

1.Жол,жылдамдық,уақыт арасындағы байланысты;

2.Қозғалыстағы денелердің ара қашықтығы ,қозғалыс уақыты ,бағыты және жылдамдығына байланысты төмендегідей қатынастарды:

2.1 Ара қашықтығы белгілі бір санға тең болатын екі пунктен бір уақытта бір біріне қарама-қарсы шыққан денелердің жылдамдығын табу.

х км/сағ у км/сағ (х+у)км/сағ жақындау жылдамдығы

2.2 Бір жерден бір уақытта шығып,қарама қарсы екі жаққа карай қозғалған денелердің алыстау жылдамдығын табу.

х км/сағ у км/сағ (х+у)км/сағ алыстау жылдамдығы

2.3 Ара қашықтығы белгілі бір санға тең болатын екі пунктен бір уақытта шығып,бір бағытта қозғалатын денелердің жақындау(егер соңғысының жылдамдығы алдыңғысынан артық болса),алыстау(егер соңғысының жылдамдығы алдыңғысынан кем болса) жылдамдықтарын табу.

х км/сағ у км/сағ (х+у)км/сағ жақындау жылдамдығы ,егер х>y

х км/сағ у км/сағ (х+у)км/сағ алыстау жылдамдығы,егер х<у болса

Есептің шарты оқылғаннан соң,есепте берілген шамалар,нені табу қажет екенін,бұдан кейін іс әрекеттің неше рет өзгеретінін анықтап,содан соң кестеде неше жол және неше баған болуы қажет екені шешіледі.[6, с. 55].

Мысалы:Бір-бірімен ара қашықтығы 50 км болатын А және В пунктерінен бір біріне қарама қарсы екі жаяу шықты. 5сағат өткен соң олар кездесті де,А-дан шыққан жаяу ары қарай жолын әуелдегіден 1км/сағ кем жылдамдықпен, ал В-дан шыққан жаяу әуелгіден 1 км/сағ артық жылдамдықпен жалғастырды. Кездескеннен кейін А-дан шыққан жаяу В-ға,В-дан шыққан жаяудың А-ға жеткен уақытынан 2 сағат бұрын жеткені белгілі болса,оның әуелгі жылдамдығы неге тең?

500км

х км/сағ (10-х) км/сағ

( 10-х) км/сағх-1 км/сағ

Есепте бір рет өзгеретін,екі түрлі екі іс-әрекет туралы айтқан, кездескенге дейінгі 1- жаяу мен 2-жаяудың іс –әрекеттері және кездескеннен кейінгі 1-жаяу 2-жаяудың іс әрекеттері. Жаяулардың кездескенге дейінгі жылдамдықтары мен кездескеннен кейінгі жылдамдықтары әр түрлі,сондықтан 1-түрлі алғашқы 2 іс-әрекет келесі 2-ші жолға жеке жазылады,демек кестеде бұған 4 жол түсініктемелер үшін 1 жол барлығы 5 жол болуы керек. Шамалар 3-уі жол,жылдамдық,уақыт,сондықтан кестеде 3 баған және түсініктеме үшін 1 баған,оған қоса кездескенге дейінгі және кездескеннен кейінгі іс-әрекеттерді бөліп көрсету үшін 1 баған арналады. Яғни кестеде барлығы 5 жол, 5 баған болуы керек.

Шамалар арасындағы байланыс:

S=v t. V= . T= .

Есептің шарты бойынша 1-жаяудың жылдамдығын табу қажет,демек оны х км/сағ деп белгілесек,екінші жаяудың жылдамдығын 500:5-10 (км/сағ ) жақындау жылдамдығынан х-ті шегеру арқылы табуға болады ,яғни 2-жаяудың жылдамдығы (10-х) км/сағ.

Кездескенге дейінгі іс-әрекетте екі жаяудың жүрген жолдары ауысады,яғни 1-жаяудың кездескенге дейінгі жолын 2-жаяудың кездескеннен кейін жүреді де,ал 2-жаяудың кездескенге дейінгі жүрген жолын 1-жаяу кездескеннен кейін жүреді және мұнда жол мен жылдамдық белгілі болады. t= формуласы бойынша уақыт табылады.

Сонымен есептің моделі төмендегідей құрылады:

жағдайлар	Іс-әрекеті	Жылдамдық(км/сағ)	Уақыт(сағат)	Жол( км)
Кездескенге дейін	1-жаяудың	х	5
	2-жаяудың	10-х	5
Кездескеннен кейін	1-жаяудың
	2-жаяудың	11-х

1-жаяу 2- жаяумен кездескеннен кейінгі жолға 2-жаяудың кездескеннен кейінгі жолға жұмсаған уақытынан 2 сағ аз жұмсағаны белгілі,демек :

- =2Жауабы :2 км/сағ

Теңдеу құру кезінде кестенің ең соңғы толтырылған бағандағы өрнектерді шамалар айтылып,кесте толтыруға пайдаланылмаған шама арасындағы байланыс пайдаланылады.

Бірігіп істелінген жұмысқа берілген есептер.

Мұнда мынадай шамалар арасындағы байланысты жақсы білу қажет.

1.А- жұмыс,n-өнімділік, t-уақыт арасындағы байланысты ;

2.Егер жұмыс көлемінің сандық шамасы берілмесе,онда толық жұмыс көлемі 1бүтінге тең болады.

Мысалы : Қуаты әр түрлі екі насос бірге жұмыс істей отыра ,бассейінді 4 сағатта толтырады. Жеке бірінші насостың бассейінді жартылай толтыруға жұмсайтын уақытты ,жеке екінші насостың бассейіннің төрттен үш бөлігін толтаруға жұмсайтын уақытынан 4 сағат артық болса , әр насос жеке жұмыс істей отыра ,бассейінді неше сағатта толтыра алады?

Есепте бес түрлі іс-әрекет қарастырылып отыр:

1-бірінші насостың жеке өзі бассейінді толтыруы ;

2-екінші насостың жеке өзі бассейінді толтыруы;

3-екі насос бірігіп бассейінді толтыруы;

4-бірінші насостың жеке өзі бассейіннің жартысын толтыруы;

5-екінші насостың жеке өзі бассейіннің төрттен үш бөлігін толтыруы.

Шамалар арасындағы қарастырылатын байланыс:

-Жұмыс ,өнімділік және уақыт.

Демек,есептің моделі төмендегідей етіліп құрылады:

Іс-әрекеті	Өнімділік(бөлікпен)	Уақыт(сағат)	Жұмыс(бөлікпен)
1-насос		х	1
2-насос		у	1
1 және 2 насос бірге		4	1
1-насос
2-насос

Алғашқы 1-3 іс-әрекеттерді қарастыра отырып ,жұмыс көлемі мен уақыт арқылы өнімділікті анықтадық,ендеше осы үш өнімділікті салыстыра отырып, бірінші теңдеуді құрамыз:

Келесі 4 және 5 іс-әрекеттерде жұмыс көлімі мен өнімділікті біле отырып , уақытты анықтадық ,олай болса бұл уақыттарды салыстыра отырып, екінші теңдеуді құрамыз.[7, б. 12].

Есептің шарты бойынша жеке бірінші насостың бассейінді жартылай толтыруға жұмсайтын уақытты,жеке екінші насостың бассейіннің төрттен үш бөлігін толтыруға жұмсатын уақыттан 4 сағат артық,ендеше екінші теңдеу төмендегідей болады:

Құрылған екі теңдеуді жүйеге бекітеміз:

Жауабы:16 сағат,5 сағат;

1. Мәселе есептер шешуде анализбен синтезді қолдану.

Мәселе есеп деп бұл арада берілгендері тек математикалық мазмұннан тұрмай сонымен бірге басқа да сюжеттен тұратын есептерді айтады. Мәтінді есеп құрғанда анализ арқылы арифметикалық аппарат көмегімен есепті шешу жоспарын құрамыз. Ал есеп көбінесе синтетикалық методпен шешіледі.

2-есеп. Үйдің үлкен бөлмесінің ені 4м, ұзындығы ал кішкене бөлменің ұзындығы 4м, ені Бір бөлменің ауданы екіншісінен қанша артық?

Анализ. Сұраққа жауап беру үшін бөлмелердің аудандарының және олардың айырмасын табу керек. Бөлмелердің аудандары оның ұзындығы мен енін көбейткенге тең.

Есептің жоспары: әрбір бөлменің ауданын тауып үлкенінен кішісін алу керек.

Синтез. 1-тәсіл 1) Үлкен бөлменің ауданы қандай?

2) Кіші бөлменің ауданы қандай?

3) Бірінші бөлменің ауданы екіншісінен қанша артық?

2-тәсіл. Үлкен бөлме ауданы екіншісі бұлардың айырмасы

2-тәсіл, синтетикалық әдіс ұтымды, бұған көбейтудің үлестірімділік заңы қолданылады.

Алгебраның есептері (теңдеулер құруға берілген есептер, теңдеулер мен олардың ситемасы, теңсіздіктер мен олардың системасы) тек анализ не тек синтез қолданылып шешіледі. Теңдеулер құрғанда алдымен белгісізден берілгенге ауысады, яғни анализ қолданылады. Теңдеулер не теңдеулер жүйесі синтез әдісі бойынша шешіледі.

3-есеп. Теплоход өзен ағысы бойынша 13 сағатта қанша км жүзсе, ол өзен ағысына қарсы 15 сағатта сондай қашықтыққа жүзді. Егер теплоходтың меншікті жылдамдығы 70км/сағ болса, онда өзен ағысының жылдамдығы қандай?

Анализ. Өзен ағысының жылдамдығын табу үшін теплоходтың меншікті жылдамдығын (70 км/сағ) және өзен ағысы не ағысқа қарсы қозғалыс жылдамдығын білу жеткілікті. Егер өзен ағысының жылдамдығы V км/сағ болса, онда теплоход өзен ағысы бойынша (70+V), ағысқа қарсы (70-V) км/сағ жылдамдықпен жүзеді. Жүрілген жолды уақытқа қатысты теңдеу ретінде өрнектейміз, яғни өзен ағысы және ағысқа қарсы жүрілген жолдардағы арақашықтықтарды теңдестіреміз.

Синтез. 15(70-V)=13(70+V) 15· 70 -15V=13·70+13V екі жағын 280 ге бөлу. 28V=(15-13)7028V=2·70 V=5.

Математикалық анализдің ең үлкен, ең кіші мәнін табуға берілген есептерде анализ, синтез қолданылады.

Өзен ағысына байланысты мәселе есептер

1-мысал. Моторлы қайық су ағысының бойымен 105 км жүргенде, осы жолды ағысқа қарсы жүзгендегіден 2 сағ жылдам жүзді. Моторлы қайықтың тынық судағы жылдамдығы 18 км/сағ болса, су ағысының жылдамдығын табыңыз.

Шешуі:

км/сағ.

Жылдымдыққа байланысты мәселе есептер

2-мысал. Ара қашықтығы 900 км екі қаладан бір-біріне қарам-қарсы екі пойыз шығып, олар жол ортада кездескен. Бірінші пойыз екіншісінен 1 сағ кеш шығып, екінші пойыздың жылдамдығынан 5 км/сағ артық жылдамдықпен жүрген. Әр поездың жылдамдығын табыңыз.

Шешуі: (км/сағ).

Жұмысқа байланысты мәселе есептер

3-мысал. Ағаш кесушілер бригадасы үш күнде 184 куб.метр отын дайындады. Бригада бірінші күні жоспарлағаннан 14 куб.метр артық, ал екінші күні 2 куб.метр кем отын дайындады. Үшінші күні бригада жоспарды 16 куб.иетр асыра орындады. Бригада жоспар бойынша күніне неше куб.метр отын дайындауға тиіс.

Шешуі: -бірінші күн, -екінші күн, -үшінші күн.

(күніне 52 куб.метр).

Химиялық концентрацияға байланысты мәселе есептер

4-мысал. Қалайы мен қорғасын қорытпасының салмағы 15 кг. Қалайының салмағы қорғасын салмағының -іне тең болса, қорытпадағы қалайы мен қорғасынның әрқайсысының салмағын табыңыз.

Шешуі: -қалайы, -қорғасын.

Бүтін сандық мәселе есептер

5-мысал. Тізбектес екі натурал санның көбейтіндісі олардың кішісінен 2 есе үлкен. Осы сандарды табыңыз.

Шешуі:

Жауабы:

6-мысал. 160 метрлік канализациялық жүйені іске қосу үшін ұзындығы 800 мм және 1200 мм 150 керамикалық трубалар пайдаланылды. Осы трубалардың әрқайсысынан қанша алынды?

Шешуі:

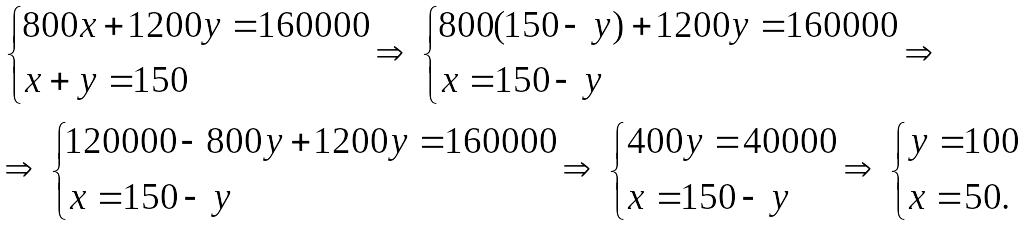
№ 14- 15Лекция.