Феррари әдісі бойынша шешу.
Теңдеудің екі бөлігін де толық квадратқа келтіру арқылы шешуге болады.
7-мысал:
теңдеуін
шешу керек.
Шешуі:
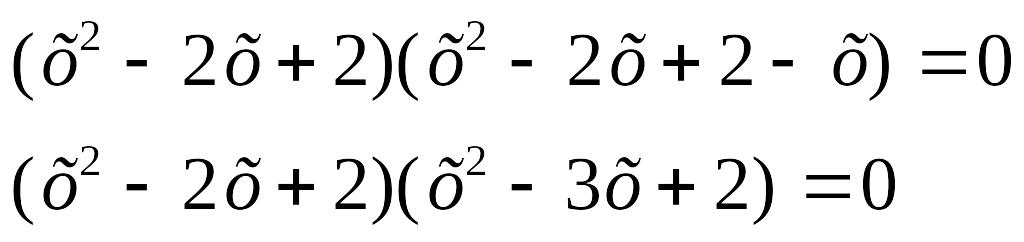
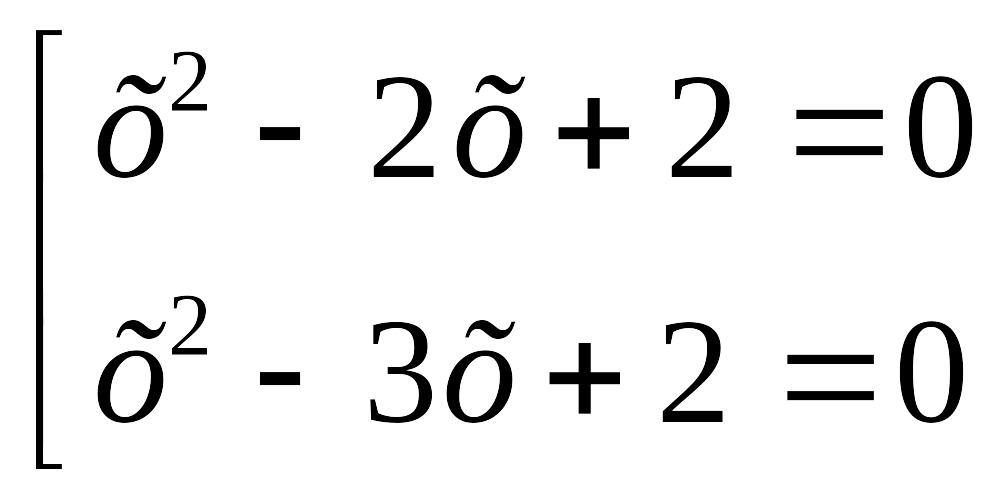
нақты
түбір болмайды.
Жауабы: х=1; x=2.
Топтау әдісі мектеп бағдарламасында қарастырылады.
5. Теңдеуді бір функцияға көбейту әдісімен шешу.
Кейде теңдеудің екі жағын бір өрнекке көбейтсек, ол қарапайым түрге келеді де, оңай шешіледі.
8-мысал:
теңдеуін
шешу керек.
Шешуі:
Теңдеудің
екі жағын да
- тің коэффициенті қандай да бір санның
кубы болатындай бір санға көбейтеміз,
2-ге көбейтейік:
Теңдеуіне
келтіріледі, енді 2х=k арқылы белгілейік,
сонда
теңдеуінен алдыңғы мысалдарды шешкендей
түбірлерін табамыз:
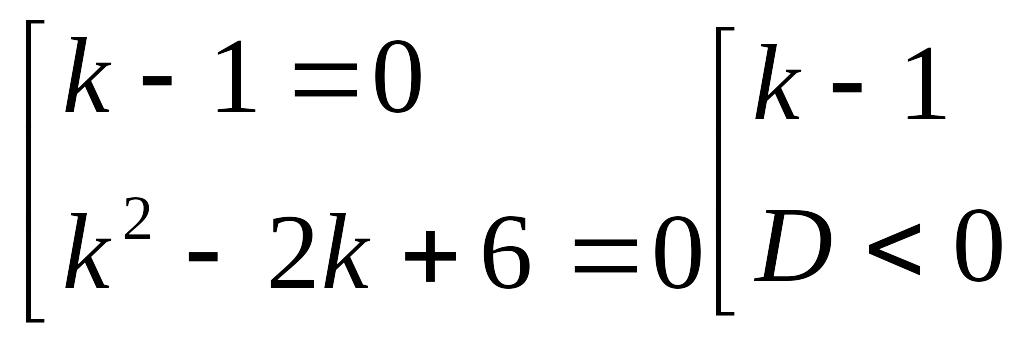нақты
түбірі болмайды.
Жауабы: х=0.
9-мысал:
теңдеуін
шешу керек.
Шешуі:
Теңдеудің
екі жағын нақты түбірлері жоқ
өрнегіне көбейтсек, берілген теңдеу
түріне келеді. Бұл теңдеудің нақты
түбірлері жоқ, демек берілген теңдеудің
де нақты түбірлері жоқ.
Жауабы: нақты түбірі жоқ.
6. Функциялардың суперпозициясын қолдану әдісімен шешу.
Егер
теңдеудің бір жағындағы функция бірнеше
қарапайым функциялардың суперпозициясы
ретінде, яғни
түрінде жазылатын болса, теңдеу оңай
шешіледі.
Бұл жағдайда мынадай теорема қолданылады.
Теорема:
Егер
монотонды өспелі функция болса, онда
және
=x теңдеулері мәндес болады.
10-мысал:
Шешуі: Теңдеуді түрлендіріп жазамыз:
Енді
бұл теңдеуде
екендігін байқауға болады, демек теңдеуді
=x
түрінде
жазуға болады. Жоғарыда
келтірілген
теореманы қолдансақ
теңдеуі шығады. Осы теңдеуден
таптық.
Жауабы:
11-мысал: теңдеуін шешу керек.
Шешуі:
Теңдеудің
екі жағын да үшінші дәрежеге шығарайық:
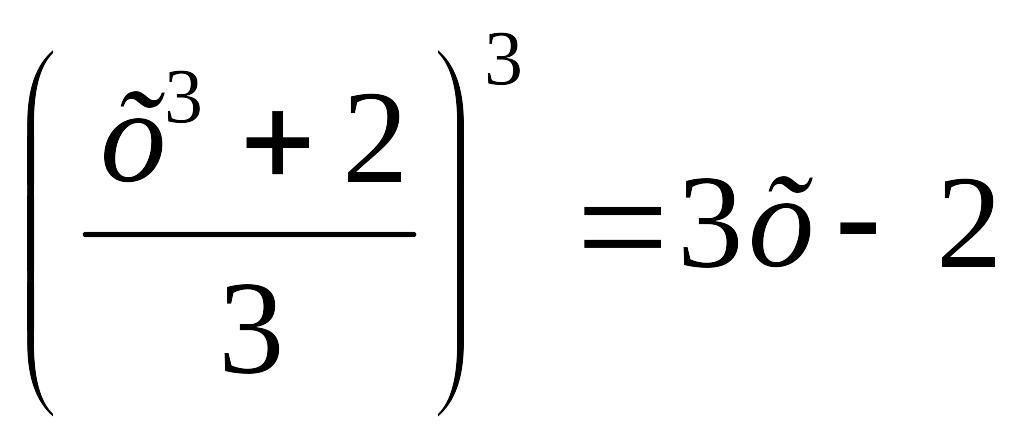немесе
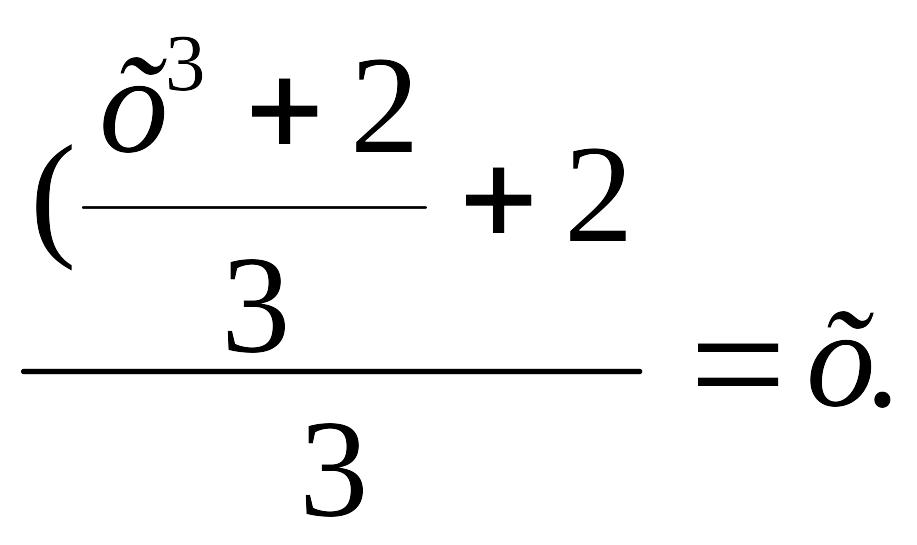Енді теореманы қолдану үшін
деп, алайық.
өспелі
функция болғандықтан
Ықшамдағаннан кейін
теңдеуіне келеміз. Топтау арқылы
теңдеудің түбірлерін табамыз:
Жауабы:
12-мысал:
теңдеуін шешу керек.
Шешуі:
деп
алайық. Теңдеуіміз
түріне келеді,
деп белгілесек,
теңдігі шығады.
функциясы
болғанда өседі. Теорема бойынша
немесе
Бұл теңдеуден
Егер
болса,
болғанда
теңдеуінің шешімі болмайды.
Жауабы:
Қорыта келгенде жоғары дәрежелі теңдеулерді шешудің әдіс-тәсілдері көп.
Теңдеудің түбірлерін анықтау, оның берілуіне және оны шешудің тиімді тәсілін іздеу, таңдау оқушылардың логикалық ойлауына, тапқырлығына байланысты.
Енді біраз есептердің шығарылуын көрсетейік:
1)
теңдеуін шешу керек.
Шешуі:
теңдеудің түбірі болады. Горнер схемасын
пайдаланамыз:
|
1 |
2 |
-5 |
-13 |
-13 |
-5 |
2 |
1 |
-1 |
1 |
1 |
-6 |
-7 |
-6 |
1 |
1 |
0 |
Сонымен
теңдеуіміз
түріне келеді.
1)
2)
деп
белгілесек,
болады, теңдеу
немесе
немесе
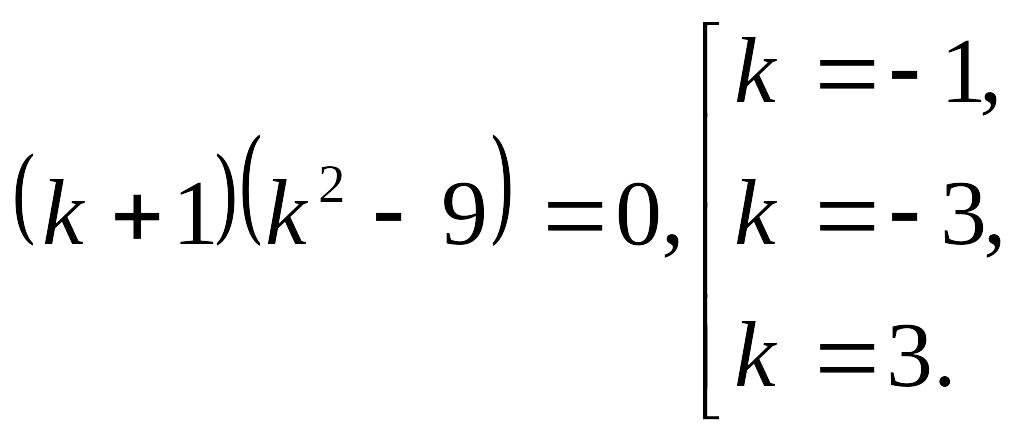
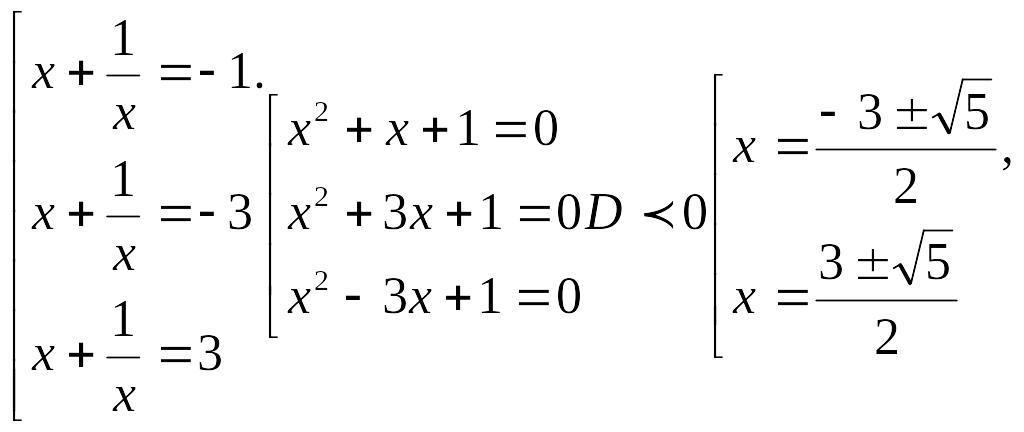
Жауабы:
2)
теңдеуінің бір түбірі
болса, қалған түбірлерін табу керек:
Шешуі:
Алгебралық теңдеудің түбірі
болса, онда екінші түбірі оның түйіндес
болады. Безу теоремасы бойынша
және
-ға
бөлінеді. Теңдеуді
- ке бөлсек:
Жауабы:
Мұндай есеп шығару жұмысын шын мәнінде «шығармашылық» жұмыс деуге болады.
Математика мұғалімінің шығармашылық іскерлігі – оқытудың өзіндік әдістері мен амалдарын табу, дәлелдерді сыни тұрғыдан талдау, есеп шығара білу, математикалық аппаратты оңай пайдалана алу қабілеті. Мұғалімді толық мағынасында өз ісінің шебері деп атау үшін оның белсенді-математикалық тәжіриесі мен шығармашылық қабілеті педагогикалық университеттің математика факультетіндегі математикадан есептер шығару курсының бағдарламасы шеңберінде, бірақ ойды шоғырландырудың жоғары деңгейін, сананың тазалығын керек ететін есептерді шығару керек.
Демек, болашақ математика мұғалімдерінің шығармашылық жағынан дайындауда жоғары дәрежелі теңдеулерді шешудің әртүрлі әдістерін үйретудің маңызы зор.
№ 13 Лекция.
Тақырыбы «Мәтіндік есептер. Мәтіндік есептердің семантикалық талдауы». Жоспар
1. Мәтіндік есептерді шешу.
2. Шешу процессінде іскерлік пен дағдыны қалыптастыру.
3. Мәтіндік есептердің семантикалық талдауы.
Бағдарламалық материялдар ішінде әсіресе мәтінді есептер оқушының ойлау қабілетіне зор ықпал етеді. Мектеп оқушылары осы тақырыпта өте қиналады. Өйткені: бағдарламада мәтіндік есептер әр кезде әр сыныпта беріледі. Математиканы оқытудың жалпы жүйесінде есептер шығару тиімді жаттығулардың бір түрі болып табылады. Алгебра практикалық есептерді теңдеулер жәрдемімен шығару тәсілдерінен туған. Теңдеулер жөніндегі ілім бүгінге дейін алгебраның мектептік курсының негізгі мазмұны болып табылады. Бірақ теңдеулерді шешу үшін бірмүшелерге, көпмүшелерге және алгебралық бөлшектерге амалдар қолдана білу керек, көпмүшелерді жіктей білуді, жақшаларды ашуды, бөлшектерді ортақ бөлімге келтіруді тағы сол сияқты амалдарды білу керек. Сөйтіп, теңдеулер жөніндегі ілімді амалдардың заңдары туралы ілімсіз игеру мүмкін емес. Теңдеулерді шешу үшін қолданылатын амалдар нақтысында сандарға қолданылады,өйткені элементар алгебрада әріптер сандарды белгілеу үшін қолданылады. Алгебраның дамуы теңдеуді алгебраның негізгі ұғымы ретінде үш негізге негізделді:
а) теңдеулер мәтінді есептерді шығарудың құралы ретінде; б) теңдеулер алгебрадағы оқу объектісі бола алатын ерекше бір формула ретінде; в) теңдеулер кеңістіктегі (жазықтықтағы) координата нүктелерін немесе сандарды жаналамай анықтайтын формула ретіндеМәтіндік есеп тек математикалық фактілермен бірге басқа да сюжеттен тұрады. Мәтінді есеп құрғанда анализ арқылы арифметикалық аппарат көмегімен есептің жоспарын құруға келеміз. Ал есеп көбінесе синтетикалық методпен шешіледі.