Формула Симпсона

На элементарном отрезке  используя значение функции в центре отрезка, заменим подынтегральную функцию  интерполяционным полиномом второй степени:

Напомним, что мы обозначили:   а значение в полуцелой точке

Вычисляя интеграл от полинома на отрезке  приходим к локальной формуле Симпсона:

                                                 (3.6)

Суммируя (3.6) по всем отрезкам, получаем формулу Симпсона для вычисления приближения к I:

                                         (3.7)

Для постоянного шага интегрирования  формула Симпсона принимает вид

            (3.8)

Замечание. Последнюю формулу иногда записывают без использования дробных индексов, в виде

       (3.8а)

К этой записи приходим, если под локальной формулой понимать результат интегрирования по паре элементарных отрезков:

где  — интерполяционный полином второй степени для  на  построенный по значениям в точках      Суммируя локальные приближения по всем парам, получим (3.8а). Разумеется, число пар на [a, b] в этом случае должно быть целым, т. е. N — четным.

Формулы, используемые для приближенного вычисления интеграла, называются квадратурными.

Численные методы решения обыкновенных дифференциальных уравнений

Методы решения ОДУ. Методы решения обыкновенных дифференциальных уравнений можно разбить на следующие группы: аналитические, приближенные и численные.

Аналитические методы позволяют получить решение в виде формулы путем аналитических преобразований. При этом имеется возможность исследовать аналитическим способом свойства общего решения и получать из него частные решения. Такие методы развиты для ряда уравнений первого порядка (с разделяющимися переменными, однородных, линейных), а также для некоторого типа уравнений высших порядков (например, линейных с постоянными коэффициентами).

Приближенные методы основаны на различных упрощениях самих уравнений путем обоснованного отбрасывания (пренебрежения) некоторых содержащихся в них членов. В некоторых случаях сначала находят точное решение упрощенной задачи, а затем приближенно вычисляют поправки, обусловленные малыми членами, отброшенными на первом этапе. На этом основаны методы теории возмущений. Другой подход связан с представлением решения в виде разложения по малому параметру, который содержится в задаче. К данной группе относятся асимптотические методы, с помощью которых получают решения, описывающие некоторую предельную картину рассматриваемого явления.

К численному решению дифференциальных уравнений приходится обращаться, когда не удается получить аналитического решения и применение приближенных методов также оказывается затруднительным. Например, внешне простое уравнение не имеет элементарного аналитического решения и может быть решено только численно. В настоящее время численные методы являются основным инструментом при исследовании большинства научно-технических задач. В основе численных методов лежат достаточно простые идеи, которые приводят к несложным математическим соотношениям. Однако практическое применение этих соотношений связано с необходимостью проведения большого объема вычислительной работы, поэтому численные методы особенно эффективны в сочетании с использованием современных компьютеров.

Наиболее распространенным и универсальным подходом к численному решению дифференциальных уравнений является метод конечных разностей. Суть этого подхода состоит в следующем. Область непрерывного изменения независимой переменной (аргумента) заменяется дискретным множеством точек, называемых узлами. Эти узлы образуют расчетную сетку. Искомая функция непрерывного аргумента приближенно заменяется функцией дискретного аргумента на заданной сетке. Эта функция называется сеточной

 27. Численные методы решения обыкновенных дифференциальных уравнений. Одношаговые методы-метод Эйлера (явный).Метод Эйлера — наиболее простой численный метод решения (систем) обыкновенных дифференциальных уравнений.

Исторически первым и наиболее простым способом численного решения задачи Коши для ОДУ первого порядка является метод Эйлера. В его основе лежит аппроксимация производной отношением конечных приращений зависимой (y) и независимой (x) переменных между узлами равномерной сетки:

где y_i+1  это искомое значение функции в точке x_i+1.

Если теперь преобразовать это уравнение, и учесть равномерность сетки интегрирования, то получится итерационная формула, по которой можно вычислить  y_i+1 , если известно y_i  в точке х_i:

                                                                           

Сравнивая формулу Эйлера с общим выражением, полученным ранее, видно, что для приближенного вычисления интеграла в (6.3) в методе Эйлера используется простейшая формула интегрирования - формула прямоугольников по левому краю отрезка.Графическая интерпретация метода Эйлера также не представляет затруднений (см. рисунок ниже). Действительно, исходя из вида решаемого уравнения (6.2) следует, что значение  есть значение производной функции y(x) в точке x=x_i -    , и, таким образом, равно тангенсу угла наклона каcательной, проведенной к графику функции y(x) в точке x=x_i.

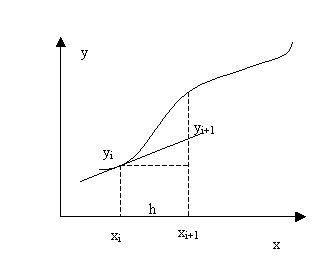
 Из прямоугольного треугольника на рисунке можно найти

  ,

откуда и получается формула Эйлера. Таким образом, суть метода Эйлера заключается в замене функции y(x) на отрезке интегрирования прямой линией, касательной к графику в точке x=x_i. Если искомая функция сильно отличается от линейной на отрезке интегрирования, то погрешность вычисления будет значительной. Ошибка метода Эйлера прямо пропорциональна шагу интегрирования:

Ошибка ~ h

Процесс вычислений строится следующим образом. При заданных начальных условиях x₀ и y₀ можно вычислить

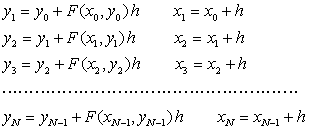
Таким образом, строится таблица значений функции y(x) с определенным шагом (h) по x на отрезке [x₀, x_N]. Ошибка в определении значения y(x_i) при этом будет тем меньше, чем меньше выбрана длина шага h (что определяется точностью формулы интегрирования).

При больших h метод Эйлера весьма неточен. Он дает все более точное приближение при уменьшении шага интегрирования. Если отрезок [x_i, x_i+1] слишком велик, то каждый участок [x_i, x_i+1] разбивается на N отрезков интегрирования и к каждому их них применяется формула Эйлера с шагом , то есть шаг интегрирования h берется меньше шага сетки, на которой определяется решение.

Численные методы решения обыкновенных дифференциальных уравнений. Модификации метода Эйлера. Неявный метод Эйлера

Медленная сходимость метода Эйлера (его погрешность убывает пропорционально лишь первой степени h) является серьезным препятствием для использования его на практике. Из рис. 5.3 видно, что один шаг по касательной к интегральной кривой приводит к значительной величине локальной погрешности l_n. Можно ли так подправить расчетную формулу метода, чтобы существенно уменьшить величину l_n?

Если у(t) — решение дифференциального уравнения y'(t)=f(t, y(t)), (5.12)

удовлетворяющее условию у(t_n)=у_п. Далее, п (5.13) - угловой коэффициент секущей, проходящей через точки (t_n, у(t_n)) и (t_n+1, y(t_n+1)) графика функции у(t) (рис. 5.5).

Ясно, что "метод", состоящий в вычислении по формуле y_п+1=y_п+hk_n, (5.14)

имеет нулевую локальную погрешность. Для того чтобы воспользоваться этой формулой, нужно лишь "научиться вычислять значение k" Интегрируя обе части уравнения (5.12) по t от t_n до t_n+1 и используя формулу Ньютона—Лейбница

Известно, что больший порядок точности имеет формула трапеций. Применяя её, получим правило трапеций:

y_n+1=y_n+h/2(f(t_n, y_n)+f(t_n+1, y_n+1)) (5.16)

Этот метод имеет второй порядок точности, но является неявным. Поэтому его реализация связана с необходимостью решения относительно y_n+1 нелинейного уравнения (5.16).

Построив на основе правила трапеций явный метод получим метод

y_n+1=y_n+h/2(f(t_n, y_n)+f(t_n+1, y_n+hf(t_n, y_n))) (5.17)

который называют методом Эйлера—Коши (или методом Хьюиа). Геометрическая иллюстрация этого метода представлена на рис.5.6. 

Вычисления разбивают на два этапа. На первом этапе (этапе прогноза) в соответствии с методом Эйлера у⁽⁰⁾_п+1=y_п+hk⁽¹⁾_n, k⁽⁰⁾_n=f(t_n, y_п) вычисляют грубое приближение к значению у(t_n+1). В точке (t_n+1, y_n+1) определяют угловой коэффициент

  k⁽²⁾_n=f(t_n+1, y⁽⁰⁾_n+1). На втором этапе (этапе коррекции) вычисляют усредненное значение углового коэффициента k_n=(k⁽¹⁾_n+k⁽²⁾_n)/2. Уточненное значение у_n+1 находят по формуле y_n+1=y_п+hk_n, что соответствует шагу по прямой, проходящей через точку (t_n, y_п) и имеющей узловой коэффициент, равный k_n.