Алгоритм решения задачи на ПК линейного программирования

1) Постановка задачи - необходимо четко определить цель задачи, дать словесное описание содержания задачи, выделить исходные данные для ее решения. Предложить общий подход к её решению, определиться какие результаты и в каком виде должны быть получены.

2) Построение математической модели - представление ее в виде формул, уравнений, соотношений, которые могут быть реализованы в компьютере.

3) Алгоритмизация - построение алгоритма.

4) Составление сценария работы на компьютере (этот этап мы пока будем опускать).

5) Написание задачи на языке программирования.

Программа должна быть универсальной (не зависящей от конкретного набора данных). Необходимо предусмотреть контроль вводимых данных. Необходимо повысить эффективность программы, т. е. уменьшить количество выполняемых операций и время работы программы.

6) Отладка и тестирование программы.

На этом этапе происходят выполнение алгоритма с помощью компьютера, поиск и исключение ошибок. При этом программисту приходится выполнять рутинную работу по проверке работы программы, поиску и исключению ошибок, и поэтому для сложных программ этот часто требует гораздо больше времени и сил, чем написание первоначального текста программы.

Программист должен составить тест - это специально подобранные исходные данные, в совокупности с результатами, которые должны получиться.

Отладка - это исправление ошибок - сложный и нестандартный процесс. Исходный план отладки заключается в том, чтобы оттестировать программу на составленных контрольных тестах.

7) Анализ полученных результатов.

Рассмотрим эти этапы на примере следующей задачи.

Задача. "Покупка в мазазине"

Человек делает в магазине покупки. Определите сколько денег у него останется после покупки в магазине перчаток стоимостью А руб., портфеля стоимостью B руб. и галстука стоимостью D руб. Все исходные данные задаются с клавиатуры.

1 этап. Постановка задачи

Исходные данные.

a - стоимость перчаток;

b - стоимость портфеля;

d - стоимост галстука;

dengi - количество денег у человека.

Все эти переменные будут вещественного типа.

Результат.

ostatok - количество денег, которое останется у человек (вещественный тип).

2 этап. Построение математической модели (метод решения)

ostatok = dengi - a - b - d

3 этап. Алгоритмизация.

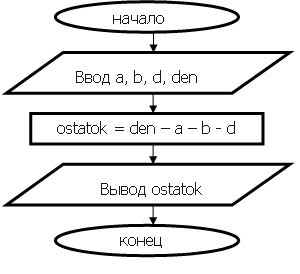
5 этап. Написание программы.

Program pokupka; Uses crt; Var a, b, d, den: real; ostatok: real; begin clrscr; write ('введите стоимость перчаток, портфеля и галстука '); readln (a, b, d); write ('введите количество имеющихся у вас денег '); readln (den); oststok := den - a - b - c; writeln ('после покупки у вас останется ', ostatok:5:2, 'руб. '); readln; end.

.Интерполяционные многочлены Ньютона. Конечные разности

Интерполяционным многочленом Ньютона называется многочлен

(31.13)

В котором I - разделенные разности различных порядков.

Этот многочлен удовлетворяет условиям

Интерполяционной формулой Ньютона называется формула

(31.14)

Замечание 1. Поскольку любой Член многочлена Ньютона зависит только от Первых узлов интерполяции и от значений функции в этих узлах, добавление новых узлов вызывает в формуле (31.13) лишь добавление новых членов без изменения первоначальных. Это является существенным преимуществом многочлена Ньютона по сравнению с многочленом Лагранжа.

Замечание 2. В силу единственности интерполяционного многочлена  Степени интерполяционный многочлен Ньютона перегруппировкой членов можно преобразовать в интерполяционный многочлен Лагранжа и обратно.

В случае равноотстоящих узлов интерполяции

| из формулы (31.14) с учетом (31.12) получается интерполяционная формула Ньютона для «интерполирования вперед»:

(31.15)

Формула (31.15) удобна при интерполировании функций для значений х, близких к наименьшему узлу

Интерполяционная формула Ньютона для «интерполирования назад»:

(31.16)

Ляционный многочлен Ньютона

Замечание 4. Раскрывая скобки и группируя члены, получаем

Пример 31.5. Найти интерполяционный многочлен Ньютона для функции По ее значениям в точках И вычислить И

Квадратурные формулы Ньютона-Котеса.

Квадратурные формулы Ньютона-Котеса. Эти формулы получены путем кусочно-многочленной интерполяции по равноотстоящим узлам. При интерполировании полиномом нулевого порядка, совпадающим с функцией в одной точке получим формулы прямоугольников

где

x_i=a+i h формула левых прямоугольников;

x_i=a+(i+1)h формула правых прямоугольников;

x_i=a+(i+0.5)h формула средних прямоугольников;

При интерполировании по двум узлам a и b полиномом первого порядка получим формулу трапеций

при произвольном числе узлов интерполирования n получим

x_i=a+i h, i=0,1,2,...n, f_i=f(xi).

Метод итерации и условия сходимости процесса Метод итерации — численный метод решения математических задач, приближённый метод решения системы линейных алгебраических уравнений. Суть такого метода заключается в нахождении по приближённому значению величины следующего приближения (являющегося более точным). Метод позволяет получить значения корней системы с заданной точностью в виде предела последовательности некоторых векторов(итерационный процесс). Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения корня x₀.

Описание метода[править | править исходный текст]

Пусть дана СЛАУ вида:  , где:

Предполагая, что   не равно 0,  . Выразим   через первое уравнение,   — через второе и т. д.  Обозначим:

,  ,  В матричном виде получим: 

За нулевое приближение примем столбец свободных членов.

 — нулевое приближение;

 — первое приближение;

 — второе приближение и т. д.;

, 

 — решение системы.

Условия сходимости процесса[править | править исходный текст]

Метод итерации применяют в случае, если сходится последовательность приближений по указанному алгоритму . Условия сходимости :   (где  =1,2,.n) или  (где  =1,2.n).

Оценка погрешности[править | править исходный текст]

, где ε -точность, x_i — вектор точных значений.

 — одна из трёх норм матрицы α,  — одна из трёх норм матрицы β.

Методы обработки и анализа экспериментальных данных. Сущность метода наименьших квадратов.

Метод наименьших квадратов (МНК, англ. Ordinary Least Squares, OLS) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функцией. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным. Пусть дана система уравнений , где  — некоторые функции,  — некоторые известные значения, x — набор неизвестных (искомых) переменных. Для произвольных значений значения отличаются от . Суть метода наименьших квадратов заключается в том, чтобы найти такие значения , при которых минимизируется сумма квадратов отклонений (ошибок)  :

В случае, если система уравнений имеет решение, то минимум суммы квадратов будет равен нулю и могут быть найдены точные решения системы уравнений аналитически или, например, различными численными методами оптимизации. Если система переопределена, то есть количество независимых уравнений больше количества искомых переменных, то система не имеет точного решения и метод наименьших квадратов позволяет найти некоторый «оптимальный» вектор . Оптимальность здесь означает максимальную близость векторов и или максимальную близость вектора отклонений к нулю (близость понимается в смысле евклидова расстояния).

В частности, метод наименьших квадратов может использоваться для «решения» системы линейных уравнений

,

где матрица не квадратная, а прямоугольная размера (точнее ранг матрицы A больше количества искомых переменных).

Такая система уравнений, в общем случае не имеет решения. Поэтому эту систему можно «решить» только в смысле выбора такого вектора , чтобы минимизировать «расстояние» между векторами и . Для этого можно применить критерий минимизации суммы квадратов разностей левой и правой частей уравнений системы, то есть . Нетрудно показать, что решение этой задачи минимизации приводит к решению следующей системы уравнений