2. Термоелектронна емісія

Н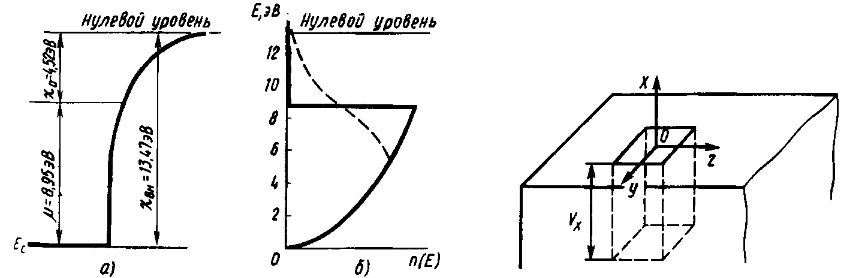 а рис. 4 показані енергетична схема вольфраму та крива розподілення електронів по енергіям при Т=0 К та за високої температури. Із рис. видно, що при підвищенні температури «хвіст» кривої розподілу заходить за нульовий рівень потенціальної ями, що свідчить про появу деякого числа електронів, що володіють кінетичною енергією, яка перевищує величину потенціального бар’єру. Такі електрони спроможні виходити із металу («випаровуватись»). Тому нагрітий метал випускає електрони. Це явище отримало назву термоелектронної емісії. Воно помітно спостерігається лише за високої температури, коли число термічно збуджених електронів, спроможних вийти із металу, виявляється достатньо великим.

Рис. 4. Енергетична схема вольфраму (а) та криві розподілу електронів по енергіям при Т=0 К (неперервна крива) та за високої температури (штрихована крива) (б).

Рис. 5. До розрахунку густини термоелектричного струму.

Помістивши поблизу нагрітого металу провідник та створивши між ним та металом поле, що збирає електрони, можна отримати термоелектронний струм. Підрахувавши густину цього струму, припускаючи, що всі емітовані електрони по зовнішньому колу повертаються до поверхні, так що електрод, що випускає електрони, залишається в цілому електронейтральним. Для цього необхідно знову розглянути розподіл електронів по швидкості всередині металу. Число електронів в одиничному об’ємі металу, складові швидкості яких лежать в інтервалах від до , від до та від до , отримаємо, помноживши число станів електрона в цих інтервалах на степінь їх заповнення. Дозволені значення хвильового вектора електрона в -просторі розподілені рівномірно, так що на кожне значення припадає об’єм (при V=1). Використовуючи співвідношення , яке для електронів зони провідності наближено виконується, то отримаємо, що дозволені значення вектора швидкості електронів рівномірно розподілені в просторі швидкостей з густиною . Густина станів із врахуванням спіну електронів має вдвічі більше значення . Ймовірність заповнення станів електронами залежить тільки від їх енергії: . Тоді число електронів в інтервалі компонент швидкостей складе:

. (2)

Виділимо на поверхні металу одиничну площадку та побудуємо на ній, як на основі, прямокутний паралелепіпед з боковим ребром (рис. 5). Число електронів в паралелепіпеді, складові швидкості яких знаходяться у вищевказаних межах, складає:

. (3)

Залишити метал можуть лише ті електрони, у яких кінетична енергія в напрямку є рівною , буде не менше висоти бар’єру , тобто ті, у яких швидкість в напрямку вісі не менша, ніж .

Інтегруючи (3) по та у межах від до (межі, у яких можуть теоретично змінюватись та ) та по у межах від до , отримаємо число електронів, які щосекундно залишають одиничну площадку нагрітого металу:

(4)

Розрахунок цього інтегралу для випадку, що реалізується на практиці, коли призводить до наступного результату:

(5)

Помноживши N на заряд електрона, отримаємо густину струму:

(6)

де

(7)

Співвідношення (6) називають формулою Річардсона-Дешмена, а коефіцієнт А – постійною Річардсона. Логарифмуючи (6), отримуємо:

(8)

Графік цієї функції зображений на рис. 6. Він уявляє собою пряму, по нахилу якої можна визначити термодинамічну роботу виходу . Екстраполюючи цю пряму до перетинання з віссю ординат, можна знайти постійну Річардсона А. При А повинна бути рівною 1,2 А/( ).

Із формули (6) випливає, що густина термоелектронного струму визначається температурою емітуючої поверхні та роботою виходу. Так як обидві ці величини стоять в показнику експоненти, то залежність струму від них дуже сильна.

Із (7) видно, що постійна Річардсона не повинна залежати від природи металу. В дійсності ж в різних металів вона різна, що частково пов’язане з різним ступенем прозорості їх потенціальних бар’єрів для електронних хвиль, що заломлюються при вильоті електронів із металу в вакуум, але в основному визначаються особливостями функції густини стану конкретних металів поблизу нульового рівня.

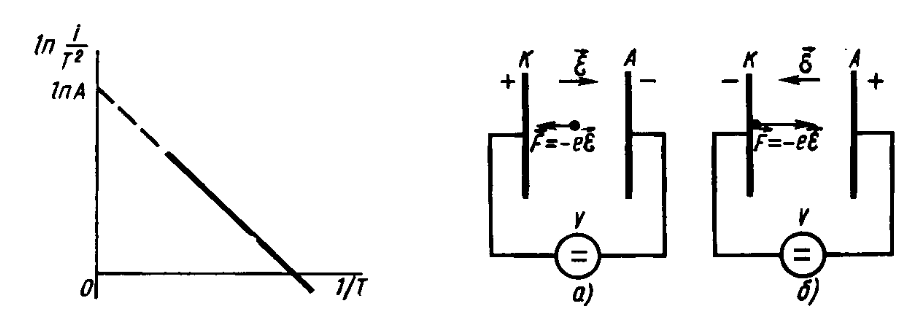
Рис. 6. Залежність густини термоелектронного струму від температури.

Рис. 7. Напрямок зовнішнього поля Е та сили F, що діє на електрон, при затримуючій (а) та прискорюючій (б) напрузі на аноді.

Якщо між емітером (термокатодом К, рис. 7, а) та колектором (анодом А) створювати різницю потенціалів V, що заважає руху електронів до колектора, то на колектор зможуть попасти лише ті електрони, які вилетіли із емітера з запасом кінетичної енергії, не меншим . Для цього їх енергія в емітері повинна бути не меншою . Замінюючи у виразі (6) на , отримаємо наступне співвідношення для струму, що тече по колу:

(9)

де S – площа поверхні, що емітує електрони; - струм емісії. Логарифмуючи цей вираз, знаходимо:

(10)

На рис. 8, а показаний графік залежності від V. Для V<0 він представляє собою пряму, що відтинає на осі ординат (V=0) відрізок .

Рис. 8. Залежність струму від напруги на аноді (а) та вплив зовнішнього поля на висоту та форму потенціального бар’єру на межі метал – вакуум.

При позитивному потенціалі на колекторі (рис. 7,б) всі електрони, що залишають емітер, потрапляють на колектор. Тому струм в колі змінюватися не повинен, залишаючись рівним струму насичення (штрихована крива на рис. 8, а).

Потрібно вказати, що подібна ВАХ спостерігається лише при відносно малій густині струму емісії та високих позитивних потенціалах на колекторі, коли поблизу емітуючої поверхні не виникає значного об’ємного заряду електронів, які не встигли дістатися колектора. Якщо такий заряд є, то вольт-амперна характеристика описується вже рівнянням Чайльда-Ленгмюра, відповідно до якого .