(1) Элементы электрической цепи (активные, пассивные)

Эл. цепью наз. совокупность устройств, предназначенных для прохождения тока и описываемых с помощью понятий тока и напряжения

Пассивные элементы. Резистивным сопротивлением наз. идеализированный элемент, обладающий только свойством необратимого рассеивания энергии.

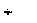
Количественной характеристикой: Сопротивление R Ом, проводимость (G=1/R, См) Математическая модель, описывающая св-ва резистивного сопротивления, определяется з-ном Ома: 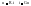Ур-ие определяет зав-сть напряжения от тока, наз. вольт-амперной х-кой (ВАХ).

Если R постоянно, то ВАХ линейна, если R зав-ит от напряжения и тока, то ВАX нелинейное Мощность в резистивном сопротивлении:

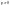
Индуктивным эл-ом наз. идеализированный эл-т эл. цепи,

обладающий только св-вом накопления им энергии магнитного поля.

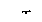
Математическая модель, описывающая св-ва индуктивного элемента

определяется соотношением 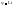где - потокосцепление

Количественная х-ка: индуктивность(положитеьлное).

Если L=сonst, зав0ость ВАХ линейная, если зав-ит от тока и напряжения- нелинейная

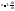мгновенная мощность:

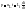
емкостным эл-от наз. идеализированный эл-т эл цепи,

обладающий только св-вом накапливать энергию эл поля.

Математическая модель, описывающая св-ва емкостного эл-та, опред-ся ВАХ: 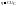Количественная х-ка: емкость (С)(положительна)

Если С=сonst, зав-ость ВАХ линейная, если зав-ит от тока и напряжения- нелинейная

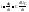Мощность:

Активные эл-ты: завис-ые и незав-ые источники эл энергии

Независимым источником напряжения наз. идеализированный двухполюсный Эл-т, напряжение на зажимах к-ого не зав-ит от протекающего через него тока. Х-ся своим задающим напряжением U_г, или ЭДС е_г ВАХ – прямая, параллельная оси токов.

Независимым источником тока наз идеализированный двухполюсный эл-т,

ток к-ого не зав-ит от напряжения на его зажимах

Х-ся своим заданный током i_г

ВАх- прямая, параллельная оси напряжения

Зависимый источник- четырехполюсный эл-т с 2-мя парами зажимов- входных и выходных Зависимые источники: источник напряжения, управляемый напряжением; источник тока, управляемый напряжением; источник напряжения, управляемый током; источник тока, управляемый током.

(2) Законы Кирхгофа. Закон Ома

1-ый з-н Кирхгофа(з-н токов): алгебраическая сумма токов ветвей, сходящихся в одном узле эл цепи,

равна нулю 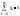, где m число ветвей, сходящихся в узле

Число независимых ур-ий =n_у-1

2-ой з-н Кирхгофа(з-н напряжений): алгебраическая сумма напряжений ветвей

в любом контуре равна нулю

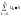
2-ой з-н Кирхгофа: (для падении янапряжений):

алгебраическая сумма падений напряжений на Эл-ах в замкнутом

контуре= алгебраической сумме ЭДС, действующих в данном контуре:

Число Ур-ий = n_в-n_у+1-n_ит

Закон Ома - это закон, устанавливающий связь между падением напряжения U на любом неразветвленном (не содержащем узлов) участке электрической цепи и величиной тока I, протекающего по этому участку.

Эта связь может быть выражена в виде математической записи или в графической форме для любого элемента электрической цепи. Графическая форма представления закона Ома называется вольтамперной характеристикой (ВАХ). Если зависимость U(I) или I(U) какого-либо элемента электрической цепи линейна, то такой элемент называют линейным, а электрическую цепь, состоящую только из линейных элементов - линейной цепью.

Для линейного элемента справедливо

U=RI или I=gU,