5. Зразок розв’язання нульового варіанта

Завдання 1. Відомо, що з 10 виробів верхнього одягу 3 не пройшли контроль якості. Навмання відібрали 5 виробів. Яка ймовірність того, що серед них є 2 вироби, які не пройшли контроль якості?

Розв’язання. Перенумеруємо всі 10 виробів. Можливими випадками будемо вважати сполучення з 10 виробів по 5, які відрізняються тільки номерами, що входять у кожне сполучення. Звідси, кількість усіх можливих випадків дорівнює кількості сполучень із 10 елементів по 5:

.

Для підрахунку можливих сприятливих випадків враховуємо, що 2 вироби, які не пройшли контроль, із 3 можна отримати = 3 способами.

Крім того, 3 вироби, які пройшли контроль якості, можна вибрати із 7 різними способами.

Кожний варіант із двох, що не пройшли контроль, комбінується із кожним варіантом із трьох минулих, отже, число кількість випадків, які сприяють появі події А, дорівнює . Звідси, шукана ймовірність .

Завдання 2. У цеху 3 верстати. Ймовірність роботи І-го дорівнює 0,9; ІІ-го – 0,8; ІІІ-го – 0,9. Обчислити ймовірність роботи: а) всіх верстатів; б) двох верстатів; в) хоча б одного верстата.

Розв’язання:

Позначимо події:

А₁ – працює І-й верстат; – відмовив І-й верстат;

А₂ – працює ІІ-й верстат; – відмовив ІІ-й верстат;

А₃ – працює ІІІ-й верстат; – відмовив ІІІ-й верстат;

Р(А₁)=0,9; Р( )=0,1

Р(А₂)=0,8; Р( )=0,2

Р(А₃)=0,9; Р( )=0,1

а) Нехай подія В – всі верстати працюють.

Ймовірність події В буде дорівнювать .

б) Нехай подія С – працюють тільки два верстати.

Подію С можливо представити у вигляді суми:

Ймовірність події С буде дорівнювати:

Враховуя, що події А_1, А_2, А₃ незалежні, а тому і незалежні і події , то можлитво застосувти теорему добутку ймовірностей:

Такким чином,

в) Нехай подія D – працює хоча б один верстат.

Ймовірність події D буде дорівнювати:

Таким чином,

Завдання 3. У кожному з 500 незалежних випробувань подія відбувається з постійною ймовірністю 0,4. Знайти ймовірність того, що подія відбувається:

а) точно 220 разів;

б) не менше ніж 180 і не більше ніж 240 разів.

Розв’язання

а) Для розв’язання цієї задачі використаємо локальну теорему Муавра–Лапласа. Задано , , .

Маємо: ;

; .

Тоді шукана ймовірність дорівнює

.

б) У цьому випадку для розв’язання застосовуємо інтегральну теорему Муавра–Лапласа. Задано , , ; .

;

.

Знаходимо значення інтегральної функції Лапласа:

; .

Шукана ймовірність дорівнює

.

Завдання 4. У кожному з 600 незалежних випробувань подія відбувається з постійною ймовірністю 0,85. Знайти ймовірність того, що відносна частота цієї події відрізняється за абсолютною величиною від імовірності 0,85 не більше ніж на 0,011.

Розв’язання. За умовою ; ; ; . Потрібно знайти ймовірність . Скористаємося формулою

.

Маємо . За таблицею значень інтегральної функції Лапласа знаходимо значення . Отже, . Шукана ймовірність приблизно дорівнює .

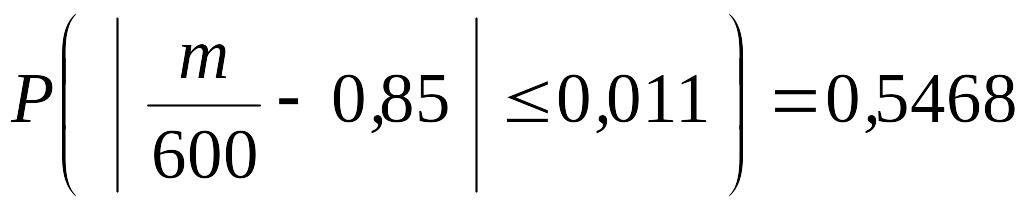Завдання 5. Задано закон розподілу дискретної випадкової величини (у першому рядку зазначено можливі значення величини , у другому – подано ймовірності цих значень). Знайти: математичне сподівання ; дисперсію ; середнє квадратичне відхилення .

	40	42	41	44
	0,1	0,3	0,2	0,4

Розв’язання. Математичним сподіванням дискретної випадкової величини називають суму добутків усіх її можливих значень на їх імовірності: .

Тоді маємо: .

Дисперсією дискретної випадкової величини називається математичне сподівання квадрата відхилення випадкової величини від її математичного сподівання: .

Маємо: .

Середнє квадратичне відхилення випадкової величини дорівнює квадратному кореню з дисперсії: .

Таким чином, .

Завдання 6. Для неперервної випадкової величини , щільність розподілу ймовірностей якої відповідає нормальному закону, задано математичне очікування і середнє квадратичне відхилення . Потрібно знайти ймовірність того, що: 1) випадкова величина набуде значення в заданому інтервалі ; 2) абсолютна величина відхилення випадкової величини від її математичного сподівання не перевищує .

Розв’язання

1) Імовірність того, що нормально розподілена випадкова величина набуде якого-небудь значення з інтервалу , обчислюється за формулою:

.

Підставивши значення, отримаємо

.

Знаходимо значення інтегральної функції Лапласа . Тоді шукана ймовірність дорівнює .

2) Імовірність того, що відхилення нормально розподіленої випадкової величини від математичного сподівання не перевищить за абсолютною величиною , обчислюється за формулою . Підставляємо значення . Значення інтегральної функції Лапласа дорівнює . Маємо ймовірність .

Завдання 7. Дано варіаційний ряд випадкових чисел із вказівкою інтервалів і частот. Знайти: 1) середнє арифметичне ; 2) дисперсію і середнє квадратичне відхилення ; 3) побудувати гістограму частот; 4) за допомогою критерію Пірсона перевірити гіпотезу про нормальний розподіл вибірки.

	2	8	20	56	12	2

Розв’язання. Статистичні дані згруповано по часткових інтервалах довжиною .

Для спрощення розрахунків при обчисленні числових характеристик емпіричного розподілу використаємо умовну варіанту , де – центральне значення (середина) -го часткового інтервалу; – деяке значення, що його набуває випадкова величина (як правило, відповідає найбільшому значенню частоти ); – довжина часткових інтервалів.

Виберемо . За умовою задачі . Тоді . За статистичним розподілом вибірки знайдемо статистичні оцінки числових характеристик випадкової величини , використовуючи аналогічні формули для умовних варіант:

; .

Перехід до значень для випадкової величини здійснюється за формулами:

; .

Усі результати розрахунків занесемо в таблицю:

№ з/п
1		30	2	-3	−6	18	0,1
2		50	8	-2	−16	32	0,4
3		70	20	-1	−20	20	1
4		90	56	0	0	0	2,8
5		110	12	1	12	12	0,6
6		130	2	2	4	8	0,1
Сума			100		−26	90

Підставляємо результати у вищезазначені формули й отримаємо:

;

.

Звідси

;

.

Середнє квадратичне відхилення дорівнює

.

Для побудови гістограми частот на осі абсцис відкладаємо задані інтервали однакової довжини і будуємо на цих часткових інтервалах як на основах прямокутники, висота яких дорівнює щільності частот .

20 40 60 80 100 120 140

Для того щоб при даному рівні значущості перевірити гіпотезу про нормальний розподіл генеральної сукупності, необхідно:

1) перейти до випадкової величини і обчислити кінці інтервалів: ; ;

2) обчислити теоретичні частоти , де – обсяг вибірки (сума всіх частот); ;

3) порівняти емпіричні й теоретичні частоти за допомогою критерію Пірсона. Для цього знаходимо спостережуване значення критерію Пірсона .

Обчислені вже значення , ; обсяг вибірки . Слід звернути увагу, що маємо два інтервали з нечисленними частотами ( ), тому об’єднаємо перший і другий інтервали, отримавши інтервал ; п’ятий і шостий інтервали, отримавши інтервал .

Результати обчислень для зручності занесемо в таблицю:

№ з/п
1		-3,55	-1,36	-0,5000	-0,4131	8,69	0,20
2		-1,36	-0,26	-0,4131	-0,1026	31,05	3,93
3		-0,26	0,83	-0,1026	0,2967	39,93	6,47
4		0,83	3,02	0,2967	0,5000	20,33	1,97

Знаходимо спостережуване значення критерію Пірсона .

Кількість степенів вільності обчислюємо за формулою , де – кількість інтервалів. Маємо .

У таблиці критичних точок розподілу за рівнем значущості і кількістю степенів вільності знаходимо критичну точку правосторонньої критичної області .

Оскільки , то гіпотезу про нормальний розподіл генеральної сукупності відкидаємо.