Гипотеза линейной регрессии

При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.

Если угловой коэффициент линии равен нулю, между   и   нет линейного соотношения: изменение   не влияет на   

Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент   равен нулю можно воспользоваться следующим алгоритмом: 

Вычислить статистику критерия, равную отношению  , которая подчиняется   распределению с   степенями свободы, где   стандартная ошибка коэффициента 

,

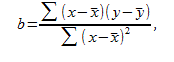
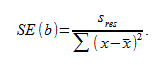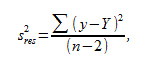 - оценка дисперсии остатков.

Обычно если достигнутый уровень значимости  нулевая гипотеза отклоняется. 

Можно рассчитать 95% доверительный интервал для генерального углового коэффициента  :

 

где   процентная точка  распределения со степенями свободы   что дает вероятность двустороннего критерия   

Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.

Для больших выборок, скажем,   мы можем аппроксимировать   значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению) 

Оценка качества линейной регрессии: коэффициент детерминации r2

Из-за линейного соотношения    и   мы ожидаем, что    изменяется, по мере того как изменяется  , и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше. 

Если это так, то большая часть вариации    будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.

Долю общей дисперсии  , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R² (в парной линейной регрессии это величина r², квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.

Разность   представляет собой процент дисперсии который нельзя объяснить регрессией. 

Нет формального теста для оценки   мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.

Применение линии регрессии для прогноза

Можно применять регрессионную линию для прогнозирования   значения по значению   в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов). 

Мы предсказываем среднюю величину   для наблюдаемых, которые имеют определенное значение   путем подстановки этого значения   в уравнение линии регрессии. 

Итак, если   прогнозируем   как   Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины   в популяции. 

Повторение этой процедуры для различных величин   позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью. 

Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.

Простые регрессионные планы

Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P, например, 7, 4 и 9, а план включает эффект первого порядка P, то матрица плана X будет иметь вид

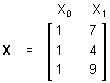
а регрессионное уравнение с использованием P для X1 выглядит как

Y = b₀ + b₁P

Если простой регрессионный план содержит эффект высшего порядка для P, например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:

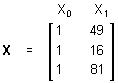
а уравнение примет вид

Y = b₀ + b₁P²

Сигма-ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X. При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X, а работать только с регрессионным уравнением.

Пример: простой регрессионный анализ

Этот пример использует данные, представленные в таблице:

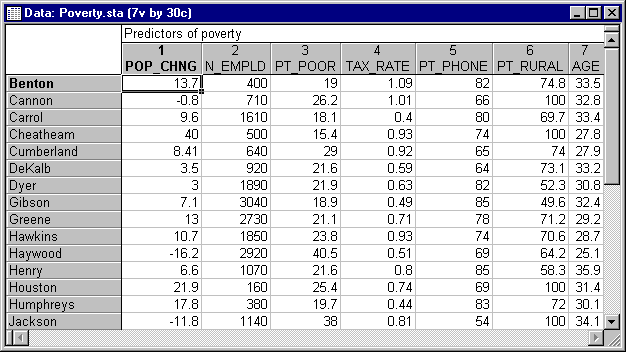
Рис. 3. Таблица исходных данных.

Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:

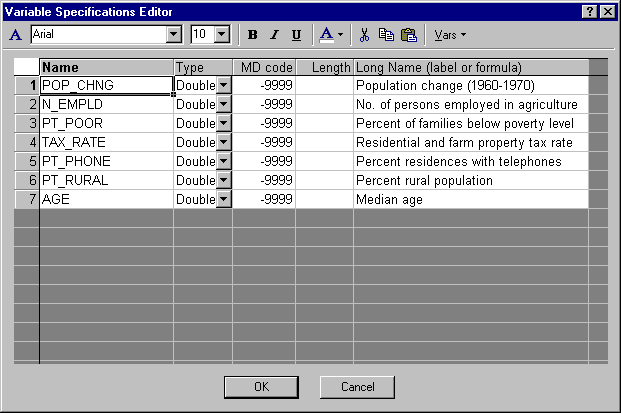
Рис. 4. Таблица спецификаций переменных.

Задача исследования

Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 (Pt_Poor) как зависимую переменную.

Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 (Pop_Chng) как переменную-предиктор.

Просмотр результатов

Коэффициенты регрессии

Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.

На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chngравен -0.40374. Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p<.05. Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение увеличение стандартного отклонения уровня бедности на .65.