П.9.2. Решение системы линейных уравнений методом исключения.

Теорема. Любая компонента искомого решения нормальной системы является решением линейного ду порядка не выше, чем n.

Доказательство. Возьмем первое уравнение нормальной системы.

продифференцируем его:

Заменим все производные искомой функции в правой части полученного равенства на пр.части уравнения исходной системы. Приведем подобные члены и опять продифференцируем уравнение. После опять заменим все производные искомой функции. Так будем поступать до тех пор, пока слева не появится производная порядка n функции 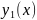. Тогда будем иметь систему линейных алгебраических уравнений: слева – производные функции , справа – искомые функции без производных с некоторыми коэффициентами.

Запишем по правилу Крамера, чему рано решение этой системы.

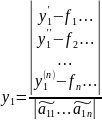
Получается, что эта функция выразится линейно через свои же производные, это равенство и есть искомое уравнение.

П.9.3. Метод Лаппо-Данилевского.

, A-матрица (постоянный коэф.)

Общее решение, если A-скаляр(некоторое число) : .

Если A – матрица, то

Если ряд сходится, то .

Алгоритм вычисления e^Ax:

1) записываем характеристическую матрицу: 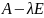и найдем минимальный полином матрицы А по формуле : 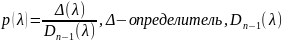- наибольший общий делитель миноров порядка n-1 характеристической матрицы.

2) найти корни минимального полинома и разложим его на множители

3) запишем общую формулу для вычисления функции от матрицы 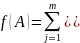некоторые постоянные матрицы.

4) найдем 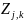из нескольких равенств, в которых f(A) для простых полиномов f( вычисленных двумя способами (заменой на А и по общей формуле).

5) вычислим фундаментальную матрицу по скалярной функции

§10. Уравнения с частными производными первого порядка.

П.10.1. Линейные уравнения с частными производными первого порядка.

Вид:

В соответствие ставится система обыкновенных ДУ в симметрической форме:

Определение. Траекторией называется график любого решения системы (2) в n-мерном пространстве, т.е. в пространстве переменных .

Определение. Первым интегралом системы (2) называется функция 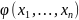принимающая постоянное значение на траекториях системы, т.е. – решение (2), то – первый интеграл (2).

Теорема 1. Функция 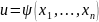– является решением уравнения (1) тогда и только тогда, когда она является первым интегралом системы (2).

Доказательство: запишем решение (2) в параметрической форме.

; и возьмем производную по t.

Производная совпадает с левой частью исходного уравнения. Если производная =0, то функция const или наоборот. Это и есть первый интеграл (2). Первые интегралы Называются независимыми, если якобиан

Теорема 2. Если независимые первые интегралы системы (2), то любое решение уравнения (1) , есть , где 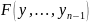некоторая дифференцируемая функция.

Доказательство:

Пусть u – некоторое решение (1). Тогда и для него будет справедливо:

(//добавить в систему еще)

Получили систему из n уравнений относительно коэф. a₁,…,a_n. По предположению все эти коэффициенты одновременно ≠0, поэтому у системы есть не нулевое решение, значит ее определитель =0.

(***) (якобиан)

Т.к. первые интегралы независимы, то 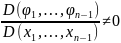. По теореме о неявной функции следует, то существует функция F(y₁,…,y_n-1) такая, что эта функция является решением уравнения (***), т.е. ч.т.д.

Если задать некоторое дополнительное условие, например условие Коши, то функция F в решение уравнения (1) может быть найдена.

Алгоритм нахождения решения с дополнительным условием:

1) Найдем первые интегралы системы (2) :

2) Запишем в них ,

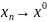3) Составим систему уравнений

– вспомогательные функции.

4) Решим эту систему относительно x₁,..,x_n-1, выразим их через

5) Получим

6) Чтобы записать решение задачи Коши удовлетворяющую условию , нужно в функцию f вместо переменных x₁,…,x_n-1 подставить , в которых заменить на , т.е.