§6 Нормальные системы ду.
П.6.1.Свойства решения нормальных систем.
(1) – в векторно -
матричной форме, где A(x)
– матрица коэф., f(x)
– вектор функция правых частей.
(2).
Система (1) неоднородная, система (2) – однородная.
1
свойство: линейная
комбинация решений (2) является решением
(2).
Доказательство: пусть y1
, y2
– решение (2). Нужно доказать, что
– тоже решение.
=>
=>
=>
– решение (2).
2 свойство: разность решений (1) является решением (2).
Доказательство: y1 , y2 – решение (1).
=>
=>
=>
– решение(2).
3 свойство: сумма решений (1) и (2) является решением (1).
Доказательство: y1 – решение (1), y2 – решение (2).
=>
=>
– решение (1).
4
свойство:
если
решение (1) с правыми частями f
1 и f
2
соответственно, то
решение
(1) с правой частью f
1 + f
2
Доказательство:
f
1 , y2
– решение (1) с f
2
.
=>
=>
– решение (1) с f
1 + f
2
.
5
свойство:
если матрица A(x)
и f(x)
непрерывны на отрезке [a,b],
то любое решение (1) удовлетворяющее
неравенству
где ||…||- норма матрицы, |…|- длина вектора.
Доказательство:
–
главное свойство нормы. Пусть y(x)
– решение (1). Тогда
.
Интегрируем от x0
до x.
согласно лемме об интегральных
неравенствах
ч.т.д.
6
свойство:
Если A(x)
непрерывна на [a,b],
x0
– некоторая точка
[a,b],
то (1) может иметь только 1 решение
удовлетворяющее условию Коши y(x0)=y0
Доказательство:
от противного. Предположим, пусть есть
y1
и y2
решение (1) удовлетворяющее y(x0)=y0.
y1(x0)-y2(x0)=0.
Из 5 свойства y1
- y2
решение (2). y(x)=
y1
- y2
.
=>
=>
ч.т.д.
7 свойство: решение (2) с непрерывной матрицей коэф. тождественно равно 0, если оно равно 0 хотя бы в одной точке.
Доказательство:
.
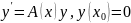Эта задача Коши имеет решение y(x)=0
.
y(x)=0
–решение. По свойству 6 – это решение
единственное.
П.6.2.Фундаментальная система решений. (фср).
Определение.
Вектор функция
– называется линейно-независимой на
[a,b],
если для
линейно-независимы
векторы
Аналогично,
.
Пусть
Определитель
– определитель Вронского.
Теорема.
Вектор функции
линейно-независим тогда и только тогда,
когда их определитель Вронского ≠0 во
всех точках отрезка.
Доказательство:
берем некоторый x
из отрезка. Допускаем, что
ЛНЗ. Тогда система уравнений
Такая система может иметь только нулевое
решение : c1=c2=…=cn=0.
Определитель этой системы, есть
определитель Вронского, поэтому если
векторы ЛНЗ то определитель≠0 и наоборот.
Определение. Фундаментальная система решений (ФСР) однородной нормальной системы ДУ называется n ее линейно независимых решений.
Теорема
2. Система решений
– система ДУ(2) фундаментальна на отрезке,
если хотя бы в одной точке x0
этого отрезка ЛНЗ векторы
.
Доказательство:
предположим, что найдется
,
что векторы
ЛЗ. Тогда существуют такие числа
c1,c2,…,cn
не все равные 0 одновременно и что
выполняется
.
Рассмотрим вектор функцию
– линейная комбинация => это решение
(2) и y(x1)=0
=> по 7 свойству y(x)=0
,
в том числе и для x0
, т.е. y(x0)=0
=> получается, что
ЛЗ (получается противоречие) =>
ЛНЗ во всех точках отрезка и система
решений фундаментальна.
Следствие: система уравнений – система ДУ(2) фундаментальна на отрезке, если хотя бы в одной точке x0 этого отрезка , определитель Вронского ≠0.
Теорема3.
Если вектор функции
– фундаментальная система решений (2),
то общее решение (2) имеет вид
,
где
произвольные
постоянные.
[
Доказательство.
Ясно, что при любом
3 решения. Любое решение y(x)
[решение (2)] можно представить в виде
(3). Пусть
)
– вектор, который можно разложить
– два решения
системы в некоторой точке.
Тогда
–
два решения системы (2), принимающие одно
и то же значение в т.
По свойству 6 они равны.
Следствие.
Если
– фундаментальная система решений
системы (2), а
– частное решение системы (1), то общее
решение системы (1) будет иметь вид
.