6. Биометрическая обработка результатов исследования

Биометрия (лат. bios – жизнь и metron – мера) обозначает измерение биологических объектов, а термин «вариационная статистика» (лат. variatio – изменение, колебание и status – состояние, положение вещей) понимается как статистическая обработка результатов измерений. Оба термина имеют недос­татки, так же как и появившийся в последние годы термин «биологическая статистика».

В связи с тем, что в настоящее время отсутствует единое общепринятое название и вместе с тем каждый из терминов имеет равное право на существование, можно избрать любой из них. Наиболее широко распространился термин «биометрия» ввиду его краткости.

Биометрия как наука сложилась на грани биологии и математики. Ее появление связано с превращением биологии из науки описательной в точную, основанную на измерениях, на применении количественных оценок при решении биологических задач. Современная биометрия – раздел биологии, который включает в себя планирование наблюдений и статистический анализ их результатов.

Использование биометрии позволяет системно подойти к анализу изучаемых явлений. Биометрия раскрывает диалектику связи между ними (взаимосвязь части и целого, единичным фактом и их совокупностью, между причиной и следствием, случайным и необходимым).

Биометрия – наука формальная, и применять ее нужно умело, с учетом специфики изучаемых явлений. Биометрия не исправит положения, если собран недоброкачественный материал или если метод анализа данных не соответствует природе изучаемых явлений. На успешное применение методов биометрии в исследовательской работе можно рассчитывать лишь при умелом, правильном ее применении. При этом не следует допускать излишеств, жонглирования биометрическими показателями там, где этого не требует дело. Не следует вдаваться и в другую крайность – ограничиваться примитивными способами анализа биометрических данных. Истина заключается не в крайностях, а в разумном подходе к делу.

При помощи биометрической обработки выявляется следующие показатели, широко применяемые в анализе результатов биологических исследований:

• среднее значение признака;

• изменчивость признака;

• показатели взаимосвязи между признаками;

• ошибки статистических величин;

• достоверность разницы между средними величинами.

В некоторых исследованиях проводится учет признаков у большого числа животных (сотни, тысячи). Обработка таких материалов представляет большую трудность в плане затрат труда и времени. Поэтому вместо данных о всем поголовье (генеральной совокупности) изучению подвергают какую-то часть (выборочная совокупность, или выборка). Она должна быть типичной, объективной, качественно однородной и как можно точнее отражать генеральную совокупность. Выборку считают большой (n > 30) и малой, если n < 30. Минимальное количество образцов или показателей, подвергаемых биометрической обработке, равно 3.

Анализ малых выборок. Определение среднего значения признака. В зависимости от цели, поставленной при анализе данных, в биометрии определяют различные средние статистические величины:

• средняя арифметическая –М – простая, взвешенная

• средняя геометрическая – G

• средняя гармоническая – Н

• средняя квадратическая – S

• мода Мо

• медиана Me.

Чаще всего используется средняя арифметическая величина М. Условное обозначение средней арифметической через М чаще применяется в биологических и педагогических исследованиях. В математической статистике предпочитают обозначение через Х. Такое обозначение в последние годы проникло и в область биологии.

Средняя арифметическая М является производной, обобщающей количественные признака ряда однородных показателей. Средняя величина ослабляет влияние индивидуальных отклонений, показывает наиболее типичное свойство изучаемого показателя.

Для вычисления простой средней арифметической суммируют показатели всех вариант V и полученную сумму делят на число вариант:

Взвешенная средняя арифметическая вычисляется в тех случаях, если значение признака (варианты) встречается неодинаковое число раз:

Пример. Определить среднюю жирномолочность коровы за 30 дней, если удой измеряли ежедневно, а процент жира – один раз в 10 дней. Исходные данные для расчёта приведены в таблице 15.

Таблица 15

Исходные данные для расчёта средней жирности молока

Дни опыта	Суммарное количество молока, кг	Содержание жира, %
1-10	50	3,2
11-20	55	зд
21-30	60	з,о

М_взв =

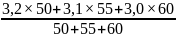
Средняя геометрическая позволяет вычислить средний прирост или снижение какого-либо показателя за определенный период времени и вычисляется по формуле:

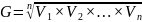
Средняя квадратическая S используется для тех признаков, которые характеризуется плоскостью круга (например, диаметр мышечных волокон, площадь колоний микроорганизмов и т.д.). Алгоритм вычислений:

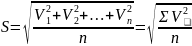
Мода Мо. Модой, или модальным вариантом, называют наиболее часто встречающееся значение признака.

Медиана Me. Медианой называют значение (или варианту) признака, которое делит всю совокупность наблюдений на две равные части, например, 1, 2, 3, 4, 5; Me = 3.

В больших выборках или в генеральной совокупности значения М, Mo, Me совпадают.

Средние значения дают общую характеристику совокупности по варьирующему признаку, но не учитывают разнообразия изучаемого признака.

Определение степени изменчивости признака. Изменчивость можно выразить следующими основными показателями: лимиты, среднее квадратическое отклонение и коэффициент вариации.

Лимиты (размах изменчивости) – это разность между максимальным и минимальным размерами признака. Лимиты показывают размах вариации (разнообразие), максимальное и минимальное значения признака.

Среднее квадратическое отклонение σ (сигма). Квадратическое отклонение обычно является более удобной характеристикой разнообразия, чем дисперсия. Сигма показывает, на сколько единиц в среднем каждая варианта отличается от средней арифметической величины, вычисленной для данной выборки (а выражается в тех же единицах, что М и С):

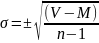
Чем больше величина σ, тем больше изменчивость признака.

Общий размах изменчивости в пределах изучаемого ряда выражается в виде М±Зσ.

По их значению можно рассчитать минимальное (М – Зσ) и максимальное (М +3σ) значения признака в данной совокупности.

Коэффициент вариации (изменчивости). Дисперсия и среднее квадратическое отклонение – величины абсолютные и выражаются в тех же единицах, что и характеризуемый признак. Поэтому сравнение степени варьирования тех или иных признаков с помощью дисперсии и среднего квадратического отклонения возможно в двух случаях. Во-первых, если величины средних арифметических сравниваемых выборок мало различаются между собой. Во-вторых, при сравнении признаков, выражаемых в одинаковых единицах измерения.

Поэтому для сравнения признаков, выраженных в разных единицах или при большом их различии, пользуются относительными показателями вариации. Одним из них является коэффициент вариации (или изменчивости) обозначается Cv, рассчитывается по формуле:

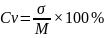
Другими словами, это отношение среднего квадратического отклонения к средней арифметической, выраженной в процентах. Коэффициент вариации позволяет сравнивать относительную изменчивость признаков, вычисленную в процентах, то есть не в абсолютных, а и относительных величи­нах. Более высокий коэффициент указывает на большую разнородность признака по сравнению с невысоким показателем Cv.

Определение взаимосвязи (корреляции) между признаками. В большинстве работ научно-исследовательского характера, в том числе и технологических, необходимо выяснение связи между отдельными признаками.

Корреляционные отношения очень широко распространены, а точнее сказать, нет ни одного признака, который мог бы проявляться совершенно изолированно.

Для выявления характера связей широко используются биометрические методы. По своему математическому выражению связи могут быть прямыми (+) и обратными (-), прямолинейными и криволинейными, простыми и множественными, могут быть связи между количественными и качественными признаками.

Взаимосвязь между признаками определяется с помощью различных показателей, из которых наиболее часто применяется коэффициент корреляции r. Он определяет силу и направление связи при прямолинейном типе связи (или близком к нему).

Коэффициент корреляции выражается десятичной дробью и может принимать значение от 0 до ±1. Знаки «+» и «-» указывают на направление связи. Чем больше значение r стремится к 1, тем больше связь между признаками. При r = 0 связь отсутствует.

Существует множество способов и формул для вычисления коэффициента корреляции. В производственных условиях в большинстве случаев проводится выборочное исследование, изучается определенным образом выбранная часть группы. Разница между сравниваемыми средними величинами в том случае достоверна, если критерий достоверности разности td равняется или больше стандартного значения критерия, определяемого по таблице Стьюдента (табл. 16).

Таблица 16

Значения критерия достоверности по Стьюденту-Фишеру при трех уровнях вероятности и разных числах степеней свободы

Число степеней свободы	Уровень вероятности						Число степеней свободы		Уровень вероятности
	0,95	0,99		0,999					0,95		0,99		0,999
	Значения								Значения
1	12,71		63,66		637	18		2,10		2,88		3,92
2	4,30		9,92		31,60	19		2,09		2,86		3,88
3	3,18		5,84		12,94	20		2,09		2,85		3,85
4	2,78		4,60		8,61	21		2,08		2,83		3,82
5	2,57		4,03		6,86	22		2,07		2,82		3,79
6	2,45		3,71		5,96	23		2,07		2,81		3,77
7	2,37		3,50		5,41	24		2,06		2,80		3,75
8	2,31		3,36		5,04	25		2,06		2,79		3,73
9	2,26		3,25		4,78	26		2,06		2,78		3,71
10	2,23		3,17		4,59	27		2,05		2,77		3,69
П	2,20		3,11		4,44	28		2,05		2,76		3,67
12	2,18		3,06		4,32	29		2,05		2,76		3,66
13	2,16		3,01		4,22	30		2,04		2,75		3,65
14	2,15		2,98		4,14	35-39		2,03		2,72		3,59
15	2,13		2,95		4,07	40-44		2,02		2,70		3,55
16	2,12		2,92		4,02	45-60		2,01		2,66		3,50
17	2,11		2,90		3,97	70-100		1,98		2,63		3,39
-						120 и >		1,96		2,58		3,29

Если td больше стандартного значения, то разница между группами достоверна, и записывается, например – Р < 0,05. Это означает, что проверяемая гипотеза может дать в 5% случаев отрицательный результат, и соответственно в 95% – положительный.

В таблице приведены значения γ и t для разного уровня достоверности. Достоверность t зависит от величины п, т.е. числа животных в выборке. Число степеней свободы у определяется так:

γ = n₁ + п₂-2.

Если критерий достоверности t_d меньше стандартного значения t, определяемого по таблице Стьюдента при уровне Р = 0,05, то разница между сравниваемыми средними недостоверна, т.е. Р > 0,05. В этом случае достоверно не доказано как наличие, так и отсутствие разницы между сравниваемы­ми средними величинами и для решения данного вопроса, возможно, требуются дальнейшие более тщательно проведенные исследования.

Следовательно, между уровнем среднесуточных приростов и затратами корма существует высокая обратная взаимосвязь.

Биометрическая обработка результатов исследований сама по себе не может повысить точности эксперимента, но она позволяет судить о достоверности проведенного опыта.

Более подробно вопросы биометрии изложены в методическом пособии Н.И. Коростелёвой, И.Е. Рабинович (1992).