Лекция №9 Тема: «Медиана и мода. Асимметрия распределения»
Второй большой класс средних величин - структурные средние, используемые для определения структуры совокупности. В отличие от степенных средних, рассчитывающихся на основе использования всех вариантов значений признака, медиана и мода характеризуют величину варианта занимающего определенное среднее положение.
Для определения понятий моды и медиана требуется определение вариационного ряда. Построение ряда представляет собой процесс упорядочивания количественного распределения элементов совокупности по значениям признака с последующим подсчетом числа элементов совокупности этими значениями.
2) ВИДЫ ВАРИАНЦИОННОГО РЯДА ПО КОЛИЧЕСТВЕННОМУ ПРИЗНАКУ:
Ранжированный ряд – распределение отдельных элементов совокупности в порядке возрастания или убывания исследуемого признака;
Дискретный ряд – распределение, основу которого составляют признаки с первым изменениям, принимающие только конечное число определенных значений;
Интервальный вариационный ряд – распределение признаков, имеющих непрерывное изменение, которые в определенных границах могут принимать любые значения.
3)МЕДИАНА (Me) представляет собой величину, соответствующую находящемуся в середине ранжированного ряда варианту.
Для нахождения медианы необходимо определить ее положения в ранжированном ряду. Положение медианы (N me) в ранжированном ряду определяется по формуле
где n – число единиц в совокупности.
В медианном интервале сумма накопленных частот превышает половину наблюдений.
Численное значение медианы определяется по формуле
Где x0 – нижняя граница интервала;
h- Величина интервала;
n – Число членов ряда;
(m – 1) – сумма накопленных членов ряда, предшествующих медианному;
N me – частота медианного интервала.
4) МОДОЙ (Mo) называют значение признака, наиболее часто встречаются у единиц совокупности.
В дискретном ряду модой будет вариант с наибольшей частотой. Для определения моды сначала определяют модальный интервал.
Модальный интервал представляет собой интервал, имеющий наибольшую частоту.
Для определения значения моды используют формулу
Где x0 – нижняя граница модального интервала;
h – Величина модального интервала;
Nm – частота модального интервала;
Nm-1 – частота интервала, предшествующего модальному;
Nm+1 – частота интервала, следующего за модальным.
Лекция №10 Тема: «Абсолютные показатели вариации. Правило сложения дисперсий»
Числовые значения признаков единиц совокупности, отличаются друг от друга, называют вариацией.
это одна из важнейших категорий, применяемых в статистической науке, под вариацией понимают изменчивость только явлений, на которые оказывают влияния неизменные в статистике не рассматриваются.
С другой стороны, под вариацией понимают изменчивость только явлений, на которые оказывают влияние внешние факторы.
1 ИСЛЕДОВАНИЕ ВАРИАЦИИ ПОЗВОЛЯЕТ:
Определить уровень зависимости изучаемого явления от прочих факторов, т.е. оценить степень устойчивости явления к внешним воздействиям;
Определить уровень однородности изучаемого явления;
Изучить явления, протекающие в обществе, характеризующиеся высоким уровнем их изменчивости.
2 ВИДЫ ВАРИАЦИЙ:
Альтернативная – признак может принять только одно из двух, противоположных по своей сути, значений. Например, население страны можно разделить на две группы: мужское и женское;
Систематическая - изменение признака в определенном направлении, не обусловленное внутренними законами развития исследуемого явления;
Случайная – изменчивость признака не предсказуема.
Показатели вариации бывают относительными и абсолютными.
3 ГРУППЫ АБСОЛЮТНЫХ ПОКАЗАТЕЛЕЙ ВАРИАЦИИ:
Размах вариации (R) показывает пределы изменчивости признака. Размах вариации представляет собой разность между максимальной величиной признака (x min):
Средние величины (групповые и общие):
Степные средние величины (средняя арифметическая, средняя гармоническая, средняя гармоническая, средняя геометрическая, средняя квадратическая и т.д.)
Структурные средние величины (мода и медиана);
Среднее линейное отклонение (d) учитывает различия всех единиц исследуемой совокупности. Данная величина определяется как средняя арифметическая из абсолютных значений отклонений, взятых по модулю, от средней. Различают простое (невзвешенное) и взвешенное среднее линейное отклонение:
Среднее линейное отклонение невзвешенное определяется по формуле:
г
де
xi-величины
совокупности;
x-средняя;
n-частота (повторяемость индивидуальных значений признака);
Среднее линейное отклонение взвешенное определяется по формуле
d = Ʃ xi-x ni .
Ʃni
Недостаток вычисления среднего линейного отклонения заключается в том, что приходится иметь дело не только с положительными, но и с отрицательными, величинами;
Дисперсии (групповая, межгрупповая и общая) среднее квадратической отключение .
Дисперсия (g²) представляет собой сумму квадратов отклонений значений показателя от средней. Различают невзвешенную и взвешенную дисперсии.
Дисперсия невзвешенная определяется по формуле
σ² =Ʃ (xi-xi)
n
Дисперсия взвешенная определяется по формуле
σ 2 = Ʃ(xi-xi)²ni
ni
Если необходимо не только изучить вариации признака совокупности, но и исследовать количественные изменения совокупности, но и исследовать количественные изменения признака по однородным группам совокупности, то помимо общей средней для всей совокупности необходимо просчитывать и частные средние по отдельным группам.
5 Виды дисперсии:
Общая характеризует изменчивость признака всей совокупности под влиянием всех определивших данную вариацию факторов.
Определяются по формуле
σ²общ Ʃ(xi-x общ)² ni
ni
где x общ- общая средняя арифметическая всей исследуемой совокупности;
средняя внутригрупповая дисперсия (gi²)показывает случайную вариацию, возникающею под влиянием неучтенных факторов. Она не зависит от положенного в основу группировки признака-фактора. Расчет дисперсии проводится в два этапа:
рассчитывается дисперсия по отдельным группам (σi²):
σi²= Ʃ(xi-xi)² ni
ni
рассчитывается средняя внутригрупповая дисперсия (σi²):
σi²=Ʃσi²Ni
ENi
Где Ni-число единиц в группе ;
между групповая дисперсия (б2) определяет возникающие под влиянием признака-фактора различия в величине исследуемого признака, так называемую системную вариацию. Рассчитывается по формуле:
δ²=Ʃ(xi-x общ)ni
ni
Где xi –средняя величина по отдельной группе.
6 Правило (закон) сложения дисперсий: сумма средней внутригрупповой дисперсии и межгрупповой дисперсии ровна общей дисперсии:
σ²общ=σ²i+δ².
Общая дисперсия возникающая под влиянием всех факторов, ровна сумме дисперсий, появляющихся как под влиянием положенного в основу группировки признака-фактора так и под влиянием других факторов.
Как следствие правила сложения дисперсий появляется положенного в основу группировки признака-фактора.
7 Среднее квадратическое отклонение (σ) представляет собой корень квадратный, извлеченный из дисперсии.
Различают простое и взвешенное среднее квадратическое отклонение.
Простое (невзвешенное)среднее квадратическое отклонение определяется по формуле
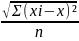
Взвешенное среднее квадратическое отклонение определяется по формуле
