Найдем уравнение траектории движения тела.

Полагая тело материальной точкой, запишем кинематические уравнения движения в проекциях на оси координат.

х (t) = v₀·cos(α)·t; (1)

у(t) = v₀·sin(α)·t – g·t²/2; (2)

Выразим время из (1) .

Сделав подстановку t в (2) получим :

y(х) = x·tg(α) – g· x²/2·[v₀·cos(α)] ²

Учитывая что , получим :

y(х) = x·tg(α)–x²·[1 + tg²(α)]·g/2·(v₀) ² = x·tg(42°)–x²·[1 + tg²(42°)]·9,81/(2·198²)= 0,9·х– x²·(1 + 0,9²)·9,81/(2·198²)= 0,9·х – 0,000226·x²

В момент времени t₁ :x(t₁) = v₀·cos(α)·t₁ = 198·cos(42°)·18,9 = 2781 м;

Построим график у(х):

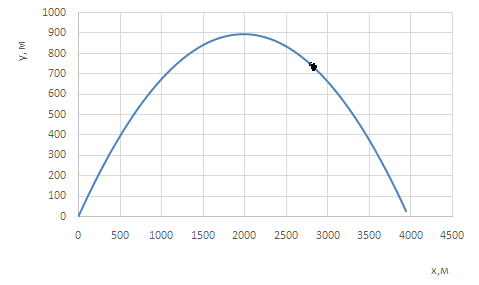
(точкой отмечено высота y[x(t₁)] тела в момент времени t₁ = 18,9 с)

6. Найдем время полета до наивысшей точки траектории t_а,полное время полёта до падения на землю ,максимальную высоту подъёма Н, дальность полёта L.

С пункта 4: 13,5 с.

= 2·13,5 с = 27 с

Максимальная высота подъема найдем с уравнения 2 пункта 5:

Н = v₀·sin(α)·t_A – g·t_A²/2 = 198·sin (42°)·13,5 – 9,8·13,5²/2 = 896 м;

Дальность полета найдем с уравнения 1 п.5:

L = v₀·cos(α)·t_В = 198·cos(42°)·27 = 3937м;

Вывод

В этой работе мы исследовали движение пульки, выпущенной со ствола пневматического пистолета под углом к горизонту; рассчитали требуемые значения:

• Определили скорость пули в момент, когда она покидает ствол- 198 м/с;

• Построили график зависимости температуры газа от номера выстрела;

• Построили график зависимости давления газа в баллончике в зависимости от номера выстрела;

• Построили графическую зависимость угла, под которым направлена скорость к горизонту, от времени в процессе всего движения тела β(t).

• Построили график траектории движения пульки и определили, что графиком траектории движения является парабола: y(х) =0,9·х – 0,000226·x², отражающая криволинейное движение пульки;указали на ней положение тела в момент времени t₁=18,9 с

• Нашли время полета до наивысшей точки траектории t_а=13,5с ,полное время полёта до падения на землю = 27 с ,максимальную высоту подъёма Н=896 м , дальность полёта L= 3937 м.

12