1. Определим скорость пули в момент, когда она покидает ствол, считая, что движение только поступательное.

Из примечания: считать, что в процессе серии выстрелов не происходит обмена теплоты с окружающей средой. То есть мы имеем дело с адиабатическим процессом, потому с 1-го начала термодинамики:

_{, где , имеем: .}

_{Во время движения пульки в стволе давление не меняется, потому можно определить работу газа, которая совершается по отношению к пульке:}

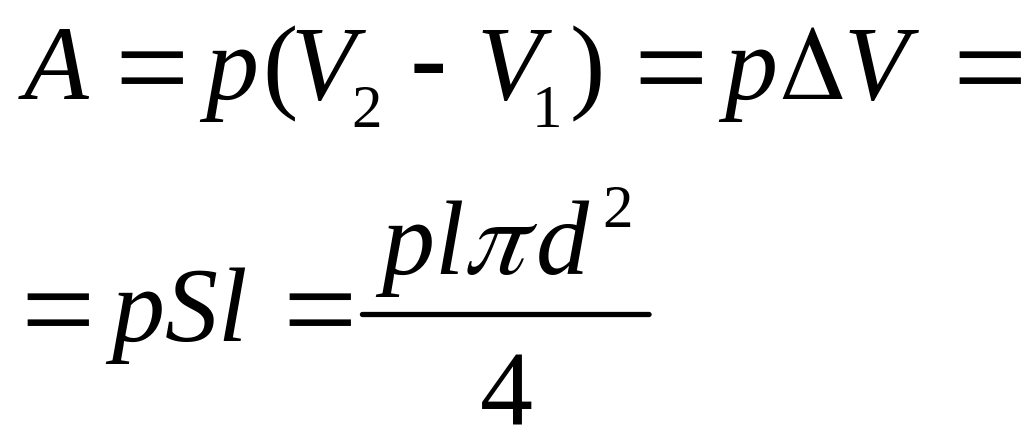
С уравнения состояния идеального газа (уравнение Менделеева-Клапейрона)

_,

_{откуда . Тогда работа газа:} .

Вся работа, выполнена газом в стволе пневматического пистолета пошла на изменение кинетической энергии пульки:

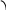
Тогда .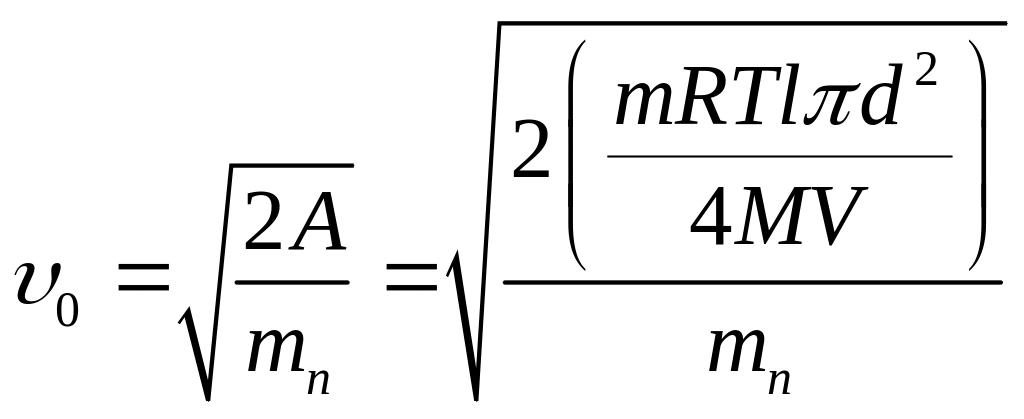

Проверкаразмерности:

Вычисление:

2. Построим график зависимости температуры газа т от номера выстрела n.

Для начала надо задать аналитически зависимость Т(N). Воспользуемся уравнением состояния идеального газа (уравнение Менделеева-Клапейрона)

_{, откуда}

В начальный момент ,где -нормальные условия. И так, после N-того выстрела будем иметь: ,(*) где у- процент расходованного газа за выстрел (у=0,035).

По скольку процесс адиабатический воспользуемся уравнением Пуассона:

. Отсюда, 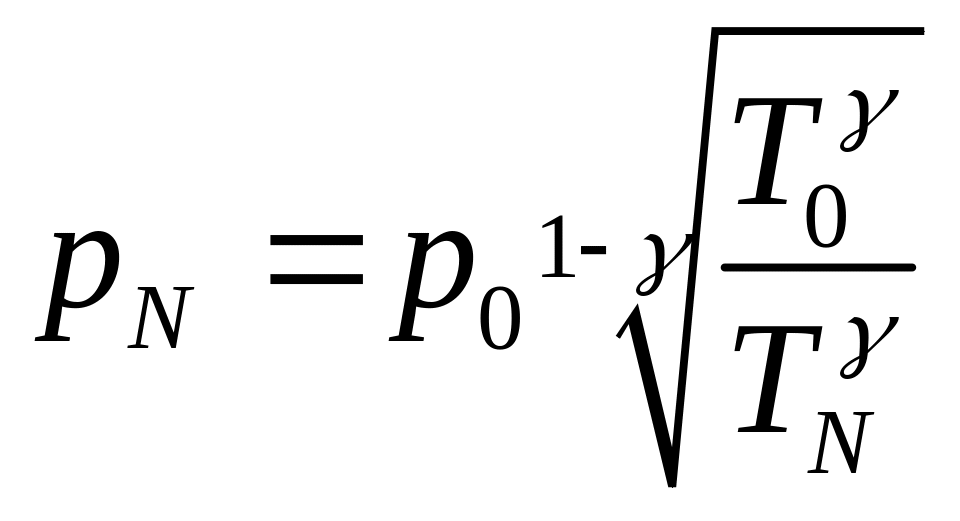(**). Подставим (**) в (*):

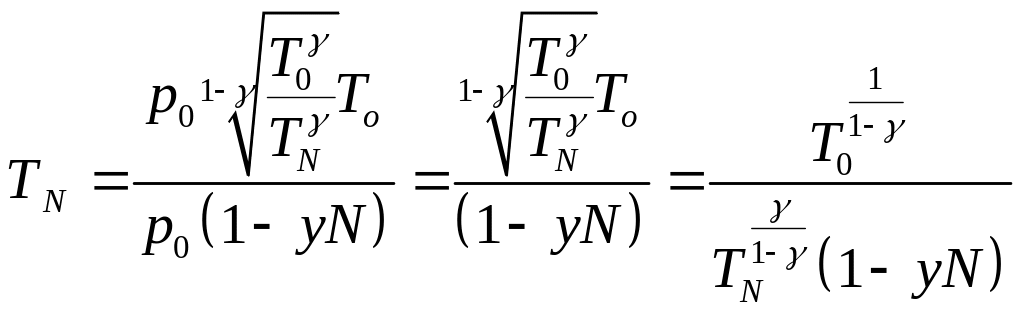. И так получаем уравнение: .

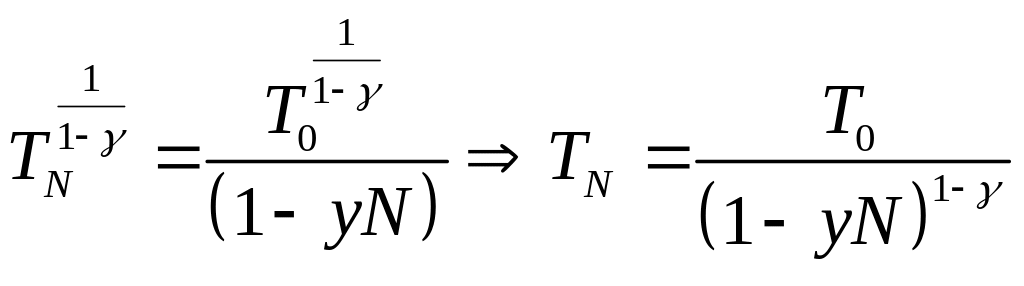Г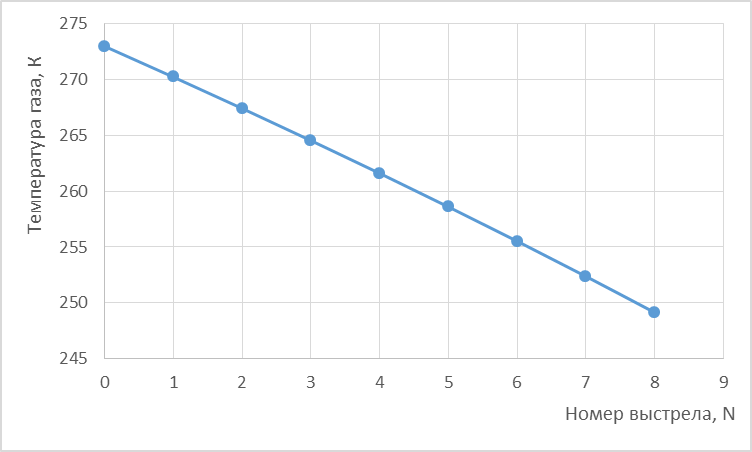 рафическая зависимость Т(N):

N	Т(N)
0	273
1	270,2422
2	267,427
3	264,5512
4	261,6115
5	258,6042
6	255,5253
7	252,3704
8	249,1345

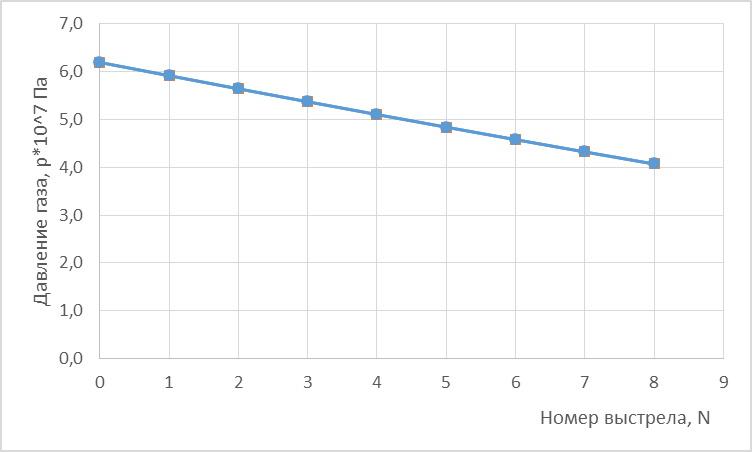
3. Построим график зависимости давления газа в баллончике р в зависимости от номера выстрела n.

С уравнения (*) выразим Р_N: . Так как , то: . И так: .

Построим график:

N	ТN	РN
0	273	6,20
1	270,2422	5,92
2	267,427	5,65
3	264,5512	5,37
4	261,6115	5,11
5	258,6042	4,84
6	255,5253	4,58
7	252,3704	4,33
8	249,1345	4,07

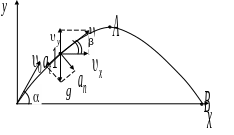
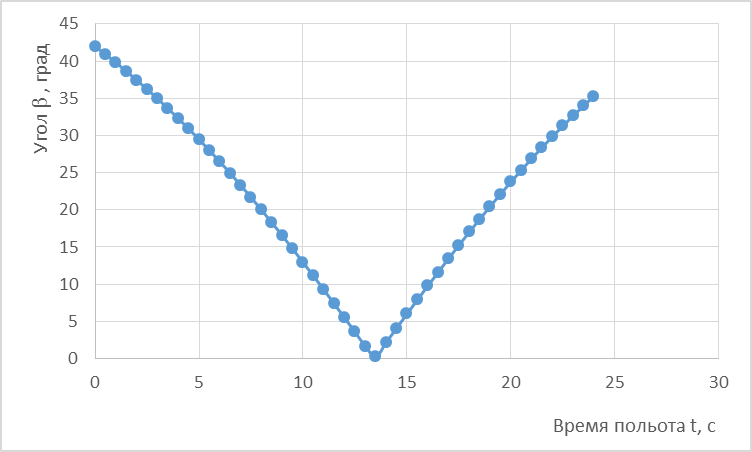
4. Построим графическую зависимость угла, под которым направлена скорость к горизонту, от времени в процессе всего движения тела β(t). Решение

Рис.1

Определим общее время полета тела . Это время равно: , где – время полета до наивысшей точки траектории . Расположим оси координат как указано на рис.1. Запишем проекции вектора скорости на координатные оси:

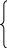
v_x(t) = v₀·cos(α);

v_у(t) = v₀· sin(α) – g·t;

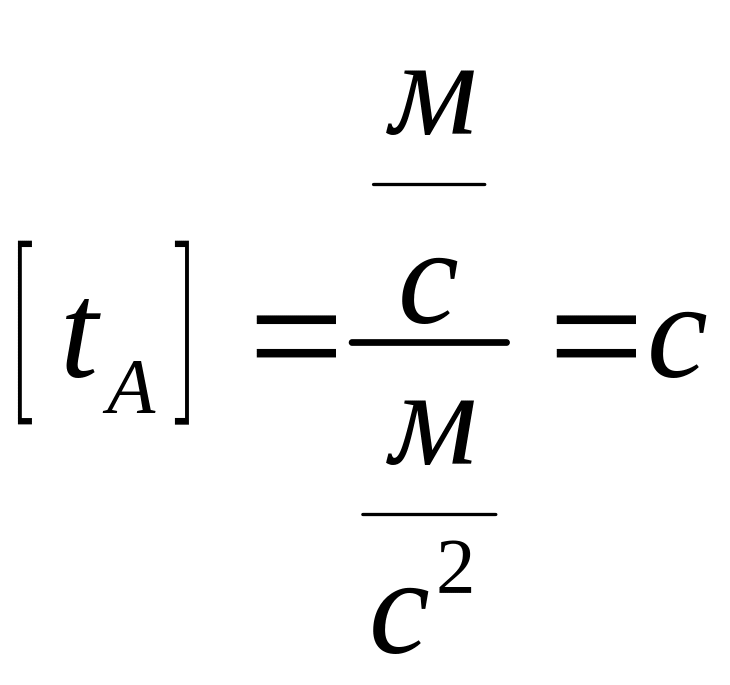
При полёте вверх тело двигается равнозамедленно с ускорением –g. Время определим из выражения : 0 = v₀·sin(α) – g·t_A, откуда . Проверка размерности: 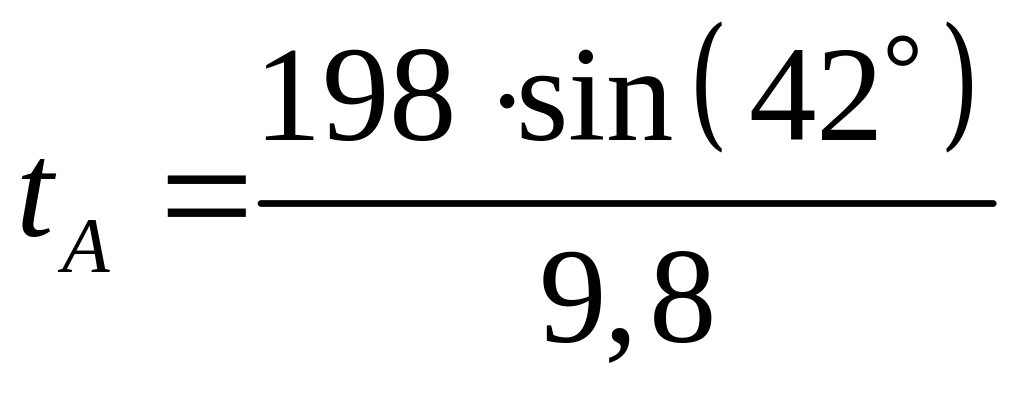≈ 13,5 с

Тогда можно найти и полное время полета тела:

= 2·13,5 с = 27 с.

_{Известно, что , где} – полная скорость тела.

В момент времени горизонтальная и вертикальная составляющие скорости тела равны :

v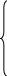 _x(t) = v₀·cos(α);

v_у(t) = v₀· sin(α) – g· t;

v(t) = =

Найдем угол β:

Виходя с того что сos (β) = = 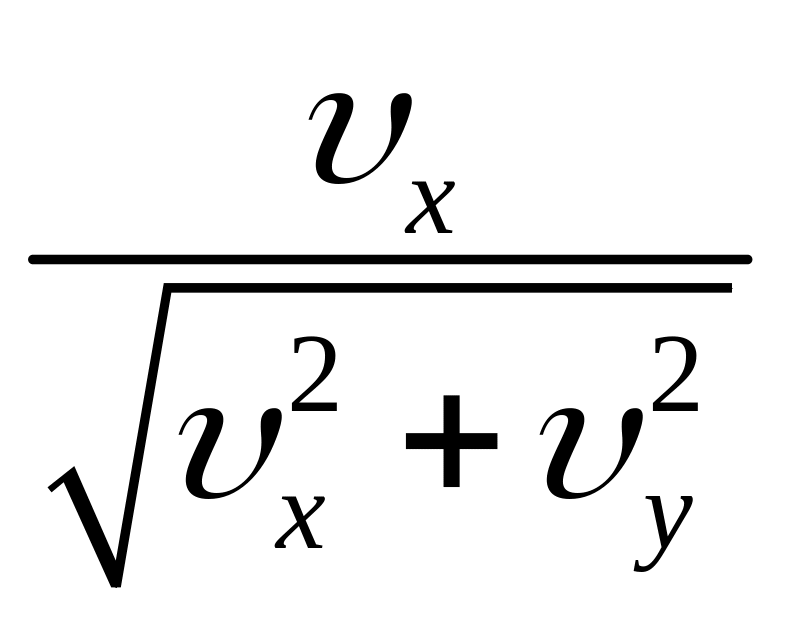имеем уравнение:

β = = = =

=· ;

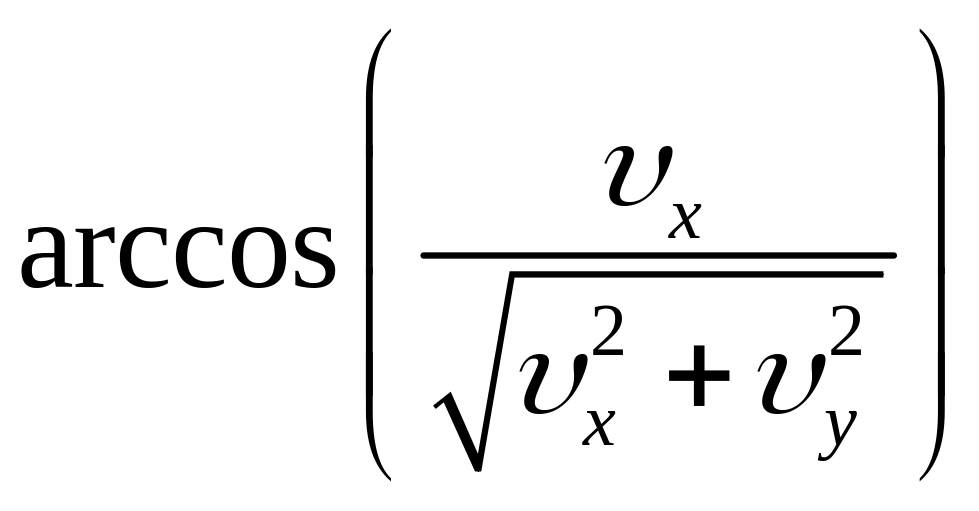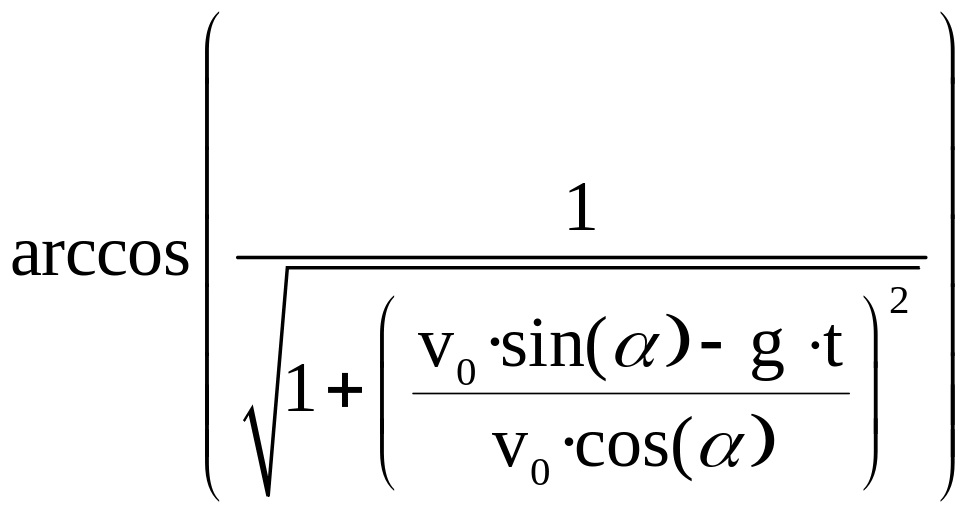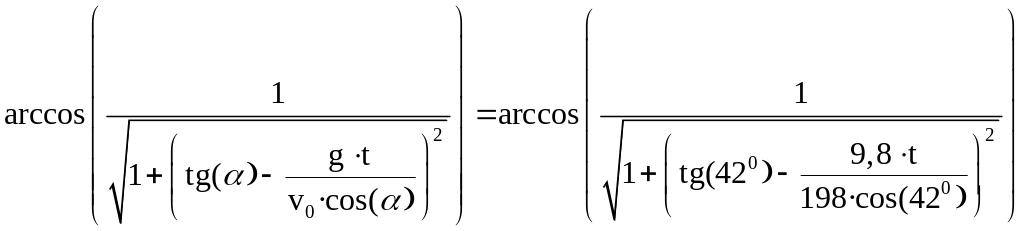И так: β =

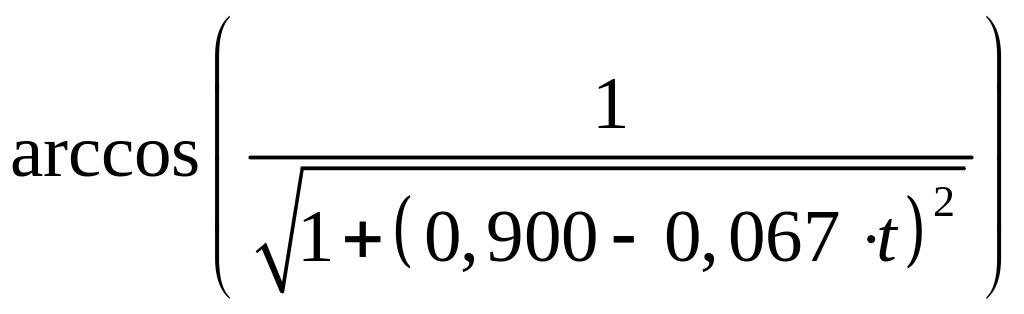
Построим зависимость β(t):

5. Построить траекторию движения тела с указанием на ней положения тела в момент времени t₁=0,7· .

Поскольку = 27 с, то t₁=0,7·27=18,9 с.