
Задачі для самостійного розв’язування Розвязати в аудиторії
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
1.1.1 |
1.1.2 |
1.1.3 |
1.1.4 |
1.1.5 |
1.1.6 |
1.1.7 |
1.1.8 |
1.1.9 |
1.1.10 |
1.1.11 |
1.1.12 |
1.1.13 |
1.1.14 |
1.1.15 |
|
1.1.11 |
1.1.12 |
1.1.13 |
1.1.14 |
1.2.16 |
1.2.17 |
1.2.18 |
1.2.19 |
1.2.20 |
1.2.21 |
1.1.6 |
1.1.7 |
1.1.8 |
1.1.9 |
1.1.10 |
|
1.2.1 |
1.2.2 |
1.2.3 |
1.2.4 |
1.2.5 |
1.2.6 |
1.2.7 |
1.2.8 |
1.2.9 |
1.2.10 |
1.2.11 |
1.2.12 |
1.2.13 |
1.2.14 |
1.2.15 |
1.1. Випишіть всі можливі підформули кожної з наступних формул (згідно до домовленості зовнішні дужки у формул опущені):
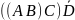

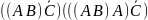
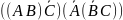



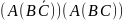
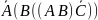
((C ÚB) ÙA) ® (((CÚA) ® B) « (A «B))
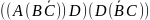

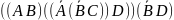
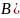
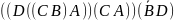
1.2. Складіть таблиці істинності для наступних формул і вкажіть, які з формул є виконуваними, які спростовними, які тотожно істинними (тавтологіями) і які тотожно хибними (запереченнями):

(P®Q) ® (Q® P)
((P®Q) ®P) ®Q
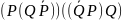

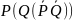
((P®Q) ®Q) ®Q
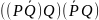
(P®Q) Ú (P® (QÙP))

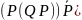
(P® (Q® R)) ® ((P® Q) ® (P® R))
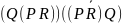
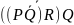
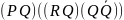
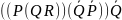
((PÚQ) ÚR) ® ((PÚQ) Ù (PÚR))
((PÚQ) Ù ((QÚR) Ù (RÚP))) ® ((PÙQ) ÙR)
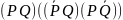
Домашнє завдання
До файлу домашнього завдання включаються приклади для самостійного розв’язування в аудиторії за своїм варіантом.
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1.8(а)
1.8(г)
1.23(а)
1.23(ж)
1.26(a)
1.26(в)
1.26(г)
1.29(а)
1.29(д)
1.29(к)
1.43(н)
1.44(б)
1.46(а)
1.47(а)
1.26(б)
1.26(д)
1.30(в)
1.30(е)
1.44(а)
1.44(в)
1.46(б)
1.46(д)
1.51(г)
1.23(а)
1.23(ж)
1.26(a)
1.26(в)
1.26(г)
1.8(а)
1.8(г)
1.8. Сформулируйте и запишите в виде конъюнкции или дизъюнкции условие истинности каждого предложения (a и b — действительные числа):
а) аb0
г) a/b= 0
1.23. Определите, является ли последовательность символов формулой:
а) ((РQ) R)͞S;
ж) ((Р (͞Q R))((͞P R)͞Q))
1.26. Составьте таблицы истинности для следующих формул и укажите, какие из формул являются выполнимыми, какие - опровержимыми, какие - тождественно истинными (тавтологиями) и какие - тождественно ложными (противоречиями):
а) (PQ)((P͞Q)͞P)
б) ((PQ)P)Q
в) (P(Q͞P))((QPQ)
г) ((PQ)Q)(PQ)
д) P(Q(PQ))
1.29 Составив таблицы истинности, докажите, что следующие формулы являются тавтологиями:
а) РР (закон исключенного третьего);
д) (PQ)(QP) (закон контрапозиции);
к) [(Р Q)R] [P(QR] (ассоциативность конъюнкции )
1.30. Составив таблицы истинности следующих формул, докажите, что все они являются тавтологиями:
в) P(Q(P Q))
е) [Р (Q R)][(Р Q) (Р R)];
1.43. Производя равносильные преобразования с использованием равносильностей из предыдущей задачи, докажите, что все формулы из задачи 1.30 являются тавтологиями.
н) ((PQ)P)P
1.44. Применяя равносильные преобразования, приведите следующие формулы к возможно более простой форме:
а) (PQ)((PQ)P);
б) (PQ)((PQ)P);
в) (PQ)(QP)(PQ)
1.46. Следующие формулы преобразуйте равносильным образом так, чтобы они содержали только операции и :
а) (X Y) (YZ);
б) (XY)(XY)
д) ((XY)(YZ))(XZ)
1.47. Следующие формулы преобразуйте равносильным образом так, чтобы отрицание было отнесено только к пропозициональным переменным и не стояло бы перед скобками:
а) ((X(YZ))Z)
1.51. С помощью равносильных преобразований докажите, что следующие формулы являются тождественно ложными (противоречиями)
г) (XY)(XY)X
Примітка. Номера задач взяті із підручника В.И. Игошин «Задачник-практикум по математической логике» . – М., 1986
