Вариант № 3655808

1. B 15 № 245180. Най­ди­те наи­боль­шее зна­че­ние функ­ции .

 

 

Ре­ше­ние.

По­сколь­ку функ­ция воз­рас­та­ю­щая, она до­сти­га­ет наи­боль­ше­го зна­че­ния в той точке, в ко­то­рой до­сти­га­ет наи­боль­ше­го зна­че­ния вы­ра­же­ние, сто­я­щее под зна­ком ло­га­риф­ма. Квад­рат­ный трех­член с от­ри­ца­тель­ным стар­шим ко­эф­фи­ци­ен­том до­сти­га­ет наи­боль­ше­го зна­че­ния в точке в нашем слу­чае — в точке −1. Зна­че­ние функ­ции в этой точке

 

Ответ: 4.

Ответ: 4

2. B 15 № 503358. Най­ди­те наи­боль­шее зна­че­ние функ­ции на от­рез­ке .

Ре­ше­ние.

Най­дем про­из­вод­ную за­дан­ной функ­ции: Най­ден­ная про­из­вод­ная по­ло­жи­тель­на при всех зна­че­ни­ях пе­ре­мен­ной, по­это­му за­дан­ная функ­ция воз­рас­та­ет. Наи­боль­шим зна­че­ни­ем функ­ции на за­дан­ном от­рез­ке яв­ля­ет­ся

 

Ответ: 42.

Ответ: 42

3. B 15 № 503318. Най­ди­те наи­боль­шее зна­че­ние функ­ции на от­рез­ке .

Ре­ше­ние.

Най­дем про­из­вод­ную за­дан­ной функ­ции:

 

 

Най­ден­ная про­из­вод­ная не­по­ло­жи­тель­на на за­дан­ном от­рез­ке, за­дан­ная функ­ция убы­ва­ет на нем, по­это­му наи­боль­шим зна­че­ни­ем функ­ции на от­рез­ке яв­ля­ет­ся

 

Ответ: 26.

Ответ: 26

4. B 15 № 26723. Най­ди­те точку ми­ни­му­ма функ­ции .

Ре­ше­ние.

Най­дем про­из­вод­ную за­дан­ной функ­ции:

 

Най­дем нули про­из­вод­ной:

 

Опре­де­лим знаки про­из­вод­ной функ­ции и изоб­ра­зим на ри­сун­ке по­ве­де­ние функ­ции:

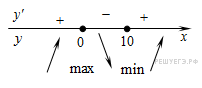
Ис­ко­мая точка ми­ни­му­ма .

Ответ: 10.

Ответ: 10

5. B 15 № 77456. Най­ди­те наи­боль­шее зна­че­ние функ­ции на от­рез­ке .

Ре­ше­ние.

Най­дем про­из­вод­ную за­дан­ной функ­ции:

 

.

Най­дем нули про­из­вод­ной:

Опре­де­лим знаки про­из­вод­ной функ­ции и изоб­ра­зим на ри­сун­ке по­ве­де­ние функ­ции:

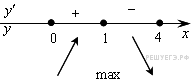
Най­ден­ная про­из­вод­ная не­от­ри­ца­тель­на на от­рез­ке [0; 1] и не­по­ло­жи­тель­на на от­рез­ке [1; 4]; за­дан­ная функ­ция воз­рас­та­ет на от­рез­ке [0; 1] и убы­ва­ет на от­рез­ке [1; 4]. В точке 1 функ­ция при­ни­ма­ет наи­боль­шее зна­че­ние. Най­дем его: .

Ответ: 1.

Ответ: 1

6. B 15 № 77440. Най­ди­те точку ми­ни­му­ма функ­ции .

Ре­ше­ние.

Най­дем про­из­вод­ную за­дан­ной функ­ции:

 

.

Най­дем нули про­из­вод­ной:

 

Опре­де­лим знаки про­из­вод­ной функ­ции и изоб­ра­зим на ри­сун­ке по­ве­де­ние функ­ции:

 

Ис­ко­мая точка ми­ни­му­ма .

Ответ: 0.

Ответ: 0

7. B 15 № 26734. Най­ди­те точку ми­ни­му­ма функ­ции .

Ре­ше­ние.

Най­дем про­из­вод­ную за­дан­ной функ­ции:

 

Най­дем нули про­из­вод­ной:

 

Опре­де­лим знаки про­из­вод­ной функ­ции и изоб­ра­зим на ри­сун­ке по­ве­де­ние функ­ции:

 

Ис­ко­мая точка ми­ни­му­ма .

Ответ: −2,5.

Ответ: -2,5

8. B 15 № 77420. Най­ди­те точку ми­ни­му­ма функ­ции .

Ре­ше­ние.

Най­дем про­из­вод­ную за­дан­ной функ­ции:

 

Най­дем нули про­из­вод­ной:

 

Опре­де­лим знаки про­из­вод­ной функ­ции и изоб­ра­зим на ри­сун­ке по­ве­де­ние функ­ции:

Ис­ко­мая точка ми­ни­му­ма .

Ответ: 4.

Ответ: 4

9. B 15 № 26725. Най­ди­те точку мак­си­му­ма функ­ции .

Ре­ше­ние.

Най­дем про­из­вод­ную за­дан­ной функ­ции:

 

Най­дем нули про­из­вод­ной:

 

Опре­де­лим знаки про­из­вод­ной функ­ции и изоб­ра­зим на ри­сун­ке по­ве­де­ние функ­ции:

Ис­ко­мая точка мак­си­му­ма .

Ответ: 10.

Ответ: 10

10. B 15 № 77428. Най­ди­те точку ми­ни­му­ма функ­ции .