Задание В 15

Вариант № 3639020

1. B 15 . Най­ди­те наи­боль­шее зна­че­ние функ­ции на от­рез­ке .

Ре­ше­ние.

Най­дем про­из­вод­ную за­дан­ной функ­ции:

 

.

Урав­не­ние не имеет ре­ше­ний, про­из­вод­ная от­ри­ца­тель­на при всех зна­че­ни­ях пе­ре­мен­ной, по­это­му за­дан­ная функ­ция яв­ля­ет­ся убы­ва­ю­щей.

Сле­до­ва­тель­но, наи­боль­шим зна­че­ни­ем функ­ции на за­дан­ном от­рез­ке яв­ля­ет­ся

 

.

Ответ: 11.

Ответ: 11

2. B 15 .

Най­ди­те наи­мень­шее зна­че­ние функ­ции .

Ре­ше­ние.

Квад­рат­ный трех­член с по­ло­жи­тель­ным стар­шим ко­эф­фи­ци­ен­том до­сти­га­ет наи­мень­ше­го зна­че­ния в точке , в нашем слу­чае — в точке −7. Функ­ция в этой точке при­ни­ма­ет зна­че­ние . По­сколь­ку ло­га­риф­ми­че­ская функ­ция с ос­но­ва­ни­ем, боль­шим 1, воз­рас­та­ет, най­ден­ное зна­че­ние яв­ля­ет­ся ис­ко­мым наи­мень­шим зна­че­ни­ем за­дан­ной функ­ции.

 

Ответ: 7.

Ответ: 7

3. B 15 . Най­ди­те наи­боль­шее зна­че­ние функ­ции на от­рез­ке .

Ре­ше­ние.

Най­дем про­из­вод­ную за­дан­ной функ­ции:

 

.

Най­дем нули про­из­вод­ной:

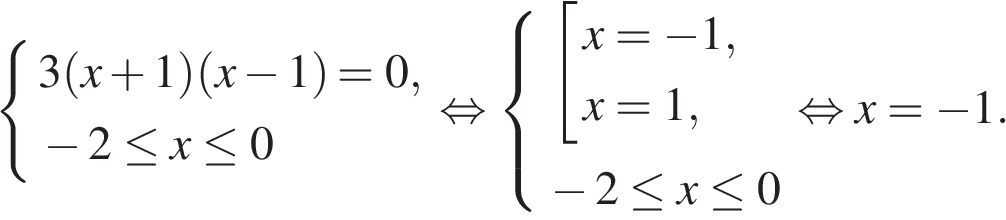
Опре­де­лим знаки про­из­вод­ной функ­ции и изоб­ра­зим на ри­сун­ке по­ве­де­ние функ­ции:

 

В точке за­дан­ная функ­ция имеет мак­си­мум, яв­ля­ю­щий­ся ее наи­боль­шим зна­че­ни­ем на за­дан­ном от­рез­ке. Най­дем это наи­боль­шее зна­че­ние:

 

.

Ответ: 6.

Ответ: 6

4. B 15 . Най­ди­те точку ми­ни­му­ма функ­ции .

 

Ре­ше­ние.

Квад­рат­ный трех­член с по­ло­жи­тель­ным стар­шим ко­эф­фи­ци­ен­том до­сти­га­ет ми­ни­му­ма в точке , в нашем слу­чае — в точке 3. По­сколь­ку функ­ция воз­рас­та­ет, и за­дан­ная функ­ция опре­де­ле­на в точке 3, она также до­сти­га­ет в ней ми­ни­му­ма.

 

Ответ: 3.

Ответ: 3

5. B 15 . Най­ди­те наи­мень­шее зна­че­ние функ­ции

Ре­ше­ние.

По­сколь­ку функ­ция воз­рас­та­ю­щая, за­дан­ная функ­ция до­сти­га­ет наи­мень­ше­го зна­че­ния в той же точке, в ко­то­рой до­сти­га­ет наи­мень­ше­го зна­че­ния вы­ра­же­ние Квад­рат­ный трех­член с по­ло­жи­тель­ным стар­шим ко­эф­фи­ци­ен­том до­сти­га­ет наи­мень­ше­го зна­че­ния в точке в нашем слу­чае — в точке  −1. Зна­че­ние функ­ции в этой точке равно

 

Ответ: 16.

Ответ: 16

6. B 15 . Най­ди­те точку ми­ни­му­ма функ­ции .

Ре­ше­ние.

За­ме­тим, что . Об­ласть опре­де­ле­ния функ­ции — от­кры­тый луч . Най­дем про­из­вод­ную за­дан­ной функ­ции:

 

Най­дем нули про­из­вод­ной:

 

Най­ден­ная точка лежит на луче . Опре­де­лим знаки про­из­вод­ной функ­ции и изоб­ра­зим на ри­сун­ке по­ве­де­ние функ­ции:

 

Ис­ко­мая точка ми­ни­му­ма .

Ответ: −6.

Ответ: -6

7. B 15 . Най­ди­те наи­мень­шее зна­че­ние функ­ции на от­рез­ке .

Ре­ше­ние.

Най­дем про­из­вод­ную за­дан­ной функ­ции:

 

Най­дем нули про­из­вод­ной на за­дан­ном от­рез­ке:

 

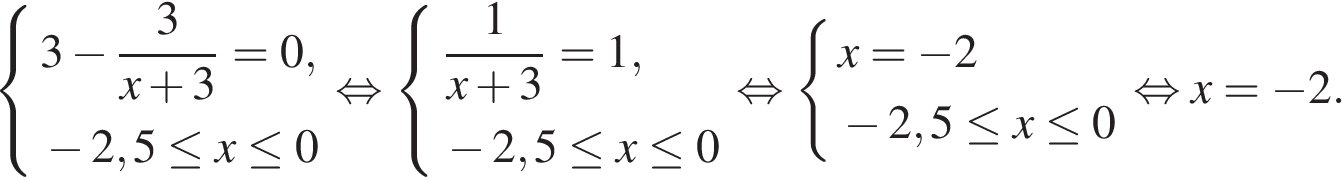
Опре­де­лим знаки про­из­вод­ной функ­ции на за­дан­ном от­рез­ке и изоб­ра­зим на ри­сун­ке по­ве­де­ние функ­ции:

 

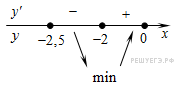
В точке за­дан­ная функ­ция имеет ми­ни­мум, яв­ля­ю­щий­ся ее наи­мень­шим зна­че­ни­ем на за­дан­ном от­рез­ке. Най­дем это наи­мень­шее зна­че­ние:

.

Ответ: −6.

Ответ: -6